Добавил:

yermolenkoigor9 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Волгоградский государственный университет

Предмет:

Технология программирования

Файл:

stohastic

.pdf

Скачиваний:

Добавлен:

18.08.2019

Размер:

908.97 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Моделирование этих и подобных им случайных величин можно осуществлять по следующей простой схеме:

M = γ , P = p0 , m = 0

		M < 0
M = M − P		M < 0	ξ = m



	M ≥ 0


P = P r(m) , m = m + 1

В качестве примера приведем вариант программной функции, осуществляющей моделирование распределения Пуассона с параметром λ :

Function Puass(Lamda : real) : integer; var

ver, p0, P : real; k : integer;

begin
k := 0;
p0 := exp(-Lamda);
P := p0;
ver := random;
repeat
ver := ver - P;
if ver >= 0 then begin
P := P*Lamda/(k+1);	{Lamda/(k+1) = r(k)}
k := k + 1;
end;
until ver < 0;
Puass := k;
end;

МОДЕЛИРОВАНИЕ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Пусть нам нужно получать значения случайной величины	ξ ,
распределенной в интервале (a, b) с плотностью вероятности	f (x) .

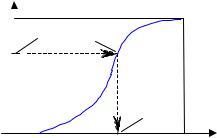
Стандартный метод моделирования основан на том, что интегральная функция распределения любой непрерывной случайной величины

равномерно

распределена в интервале

(0,1),

т.е. для любой случайной

величины

с плотностью распределения

f (x)

случайная величина

F(y)

F( y) = ∫ f (x) dx

1.0

равномерно

распределена

на

0.8

F(ξ) = γ

интервале (0,1).

0.6

Тогда случайную величи-

0.4

ну

с произвольной плот-

0.2

ностью распределения

f (x)

можно найти

следующим

образом:

1. Получаем случайную величину γ

, равномерно распределенную в

интервале (0,1).

2. Полагаем F(ξ) = ∫ f (x) dx = γ .

3. Решая уравнение ξ = F −1(γ) , находим искомое значение

ξ .

Такой способ получения случайных величин называется методом

обратных функций.

В качестве примера рассмотрим получение случайной величины

τ ,

имеющей экспоненциальное распределение с плотностью

p(τ) = λ e−λτ ,

где

−

параметр

распределения.

Такое

распределение

широко

используется при моделировании различных физических явлений: это и длина свободного пробега ионизирующих частиц в веществе, и распределение интервалов времени между моментами попадания ионизирующих частиц в регистрирующий прибор и т.д..

Следуя указанной методике, получаем

∫ λ e−λx dx = 1− e−λτ = γ .

0
Отсюда	τ = −	1	ln(1− γ) . Так как величина	1− γ	распределена
Отсюда	τ = −	λ	ln(1− γ) . Так как величина	1− γ	распределена
		λ

точно так же, как и γ , то последнюю формулу можно переписать в виде

τ = −	1	ln(γ) .
τ = −		ln(γ) .
	λ
Еще один пример.							Пусть требуется получить случайную величину ξ ,
распределенную в интервале (a,b)									с равномерной плотностью:
p(x) =			1		,		a < x < b .
p(x) =			b − a		,		a < x < b .
			b − a
			ξ	dx			ξ − a
Тогда			∫	dx		=	ξ − a	= γ	и мы получаем следующее выражение:
Тогда			∫	b − a		=		= γ	и мы получаем следующее выражение:
			a	b − a			b − a
			a
ξ = a + γ (b − a) .						Эта формула часто используется для расширения или

смещения стандартного интервала (0,1) равномерно распределенной случайной величины до необходимого интервала (a, b) .

Следует отметить, что не всегда возможно так легко разрешить получаемые уравнения. Чаще всего аналитическое решение не существует, и

тогда приходится прибегать к численному решению уравнения ξ = F −1(γ) . Может оказаться и так, что алгоритм численного решения указанного уравнения будет достаточно сложным или требовать заметных затрат времени на вычисления. Тогда могут быть использованы другие методы

генерирования случайных

величин.

Среди

этих методов отметим

метод

исключения.

Суть метода исключения (или метода Неймана) заключается в

следующем.

Пусть случайная величина

определена

на

конечном

интервале

( a,b )

плотность

f(x)

ее

распределения ограничена,

так

что

f (x) ≤ M

Тогда,

используя

пару

равномерно

распределенных

на

интервале

(0,1) случайных

чисел

γ ,

ξ0

осуществляем

следующие

действия

для

розыгрыша

значения

ξ :

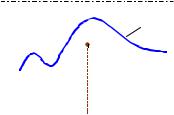
1. Разыгрываем два значения

γ1 и

γ2

случайной величины

строим случайную точку Q с координатами (см. рисунок):

ξ0 = a + γ1 (b − a) , η = γ2 M .

2. Если

η > f (ξ0 )

, то пару значений (γ1, γ2 ) отбрасываем и переходим

к п.1;

иначе принимаем

ξ = ξ0 .

Таким образом, мы определяем координаты случайной точки

Q(ξ0 , η)

и, если точка окажется

под

кривой

f (x) , то

абсцисса этой

точки

принимается в качестве значения случайной величины

ξ = a + γ1 (b − a)

плотностью распределения f (x) . В противном случае точка отбрасывается, мы определяем координаты следующей точки, и все повторяется.

Существуют и другие многочисленные способы формирования случайных величин с различными определенными законами распределения. Так, например, моделирование нормально распределенной случайной

величины X может быть осуществлено на основании центральной предельной теоремы теории вероятностей. Эта теорема утверждает, что закон распределения суммы независимых случайных величин стремится к

нормальному	при	увеличении		числа	слагаемых.		Для	практического
									n
использования	можно		считать,	что	случайная	величина			X = ∑γi
									i=1
распределена	нормально при			n ≥ 8	с математическим				ожиданием
M{X }= n / 2	и среднеквадратичным отклонением					σ =	n 12 .
Так как моделирование любого нормального распределения с
параметрами	(m, σ) может быть осуществлено по очевидной формуле
ξ = m + σ η ,	где	η	− нормальна с		параметрами		(0,1),	то	нормально

распределенные случайные величины с параметрами (0,1) можно вычислять по следующей приближенной формуле:

η =	12	1 2
η =	n
	n
При	n = 12

	n	1
	∑γi −
	∑γi −	2	n .
i=1		2

эта формула заметно упрощается: η = ∑γi − 6 .

i=1

ОБРАБОТКА РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ

Чтобы получить статистические характеристики исследуемой модели, необходимо производить обработку результатов моделирования. Обработки могут быть различными в зависимости от цели моделирования, но чаще всего бывает необходимо определить математическое ожидание (среднее значение) и дисперсию (среднеквадратичное отклонение) интересующей нас величины (величин).

При реальном моделировании, как и в реальных экспериментах, мы всегда имеем дело с конечным числом испытаний или опытов, то есть с

конечным числом n значений любой случайной величины X . Для определения средних значений и дисперсий можно воспользоваться стандартными приемами статистической обработки экспериментальных

данных для оценок среднего и дисперсии

по

выборке из

n значений

x1, x2 , , xn

случайной величины

X :

выборочное среднее:

∑xi

i=1

выборочная дисперсия:

σn2

∑(xi

− xn )2 .

n −1

i=1

Величина xn

называется выборочным средним, а

σn2

− выборочной

дисперсией случайной величины X .

Значения

и σn2

можно принять в

качестве оценок математического ожидания

M{X }

и дисперсии D{X }

величины

X , т.е.

M{X }≡ x ≈ xn

D{X }≡ σ2 ≈ σn2

. Приближенные

равенства становятся точными в

пределе,

когда

n → ∞ .

Выборочное

среднеквадратичное

отклонение

σn

равно

корню

квадратному из

выборочной дисперсии σ2n .

Оценки среднего и дисперсии могут производиться как после проведения моделирования, так и параллельно ему. В первом случае обработке подвергается достаточно большой массив накопленных чисел, во втором − каждое из значений случайной величины используется сразу же после получения. Если при решении задачи моделирования достаточно лишь вычисления значений среднего и дисперсии случайной величины, то определение их значений в процессе моделирования существенно сокращает как время вычислений, так и требуемый объем памяти (всего две переменных

для определения значений xn и σ2n ). Для этого нужно переписать формулу для определения дисперсии в эквивалентной форме:

∑

− x

)

∑

− n x

n −1

i=1

Тогда

при

получении

каждого

нового

значения

случайной

величины

достаточно определять сумму

∑xi

значений случайной

i=1

величины и сумму

∑xi2

значений квадратов случайной величины.

i=1

Часто желательно и удобно иметь возможность графически отображать получаемую информацию о распределении моделируемой случайной величины, например, в виде гистограммы или графика так называемого частотного распределения. Для этого диапазон всех возможных значений случайной величины разбивают на одинаковые (как правило) интервалы, внутри которых сосредоточены статистические данные. Интервалы не должны перекрываться. Внутри каждого интервала определяют частоту попадания в него значений случайной величины. Число интервалов и их ширина чаще всего определяются сущностью задачи, однако они должны быть достаточно большими, чтобы не упустить важные подробности в поведении случайной величины. Обычно число интервалов выбирают порядка 20 или больше.

Для построения гистограммы нужно над каждым отрезком оси абсцисс, соответствующим выбранному интервалу значений случайной величины, построить прямоугольник, площадь которого пропорциональна количеству попаданий значений случайной величины в данный интервал. При интервалах равной ширины частота попаданий будет пропорциональна высоте прямоугольника.

Рассмотрим следующий простой пример. Пусть у нас есть набор резисторов с номиналом сопротивления Rnom . Резисторы имеют разброс

значений сопротивлений ∆R , так что истинная величина сопротивления любого резистора с равной вероятностью может находиться в диапазоне от Rnom − ∆R до Rnom + ∆R . Нужно смоделировать измерение значений

{для накопления суммы значений сопротивлений} {для накопления суммы квадратов значений

сопротивлений}

сопротивлений для

Nizm

резисторов, определить среднее значение и

среднеквадратичное отклонение сопротивлений, и построить гистограмму распределения значений сопротивлений. Это можно смоделировать следующей программой:

uses Gisto,Graph;

const

NGist = 100; { число интервалов гистограммы } var

Gd, Gm, i : Integer; Nizm : integer;

R, Rnom, Rsr, SumR, SumR2, deltaR, Disp : real;

begin

write('Введите номинал сопротивления Rnom = '); readln(Rnom);

write ('Введите величину разброса deltaR = '); readln (deltaR);

write ('Введите число сопротивлений Nizm = '); readln (Nizm);

SumR := 0;

SumR2 := 0;

{Инициализация гистограммы } InitGist(NGist,Rnom-deltaR,Rnom+deltaR);

{Моделирование измерения сопротивлений }

Randomize;
for i := 1 to Nizm do begin
R := Rnom + (2deltaRRandom-deltaR);		{ R = Rnom + DR }
SumR := SumR + R;		{ Для определения среднего }
SumR2 := SumR2 + sqr(R);		{ и дисперсии измерений }
InGist(R);		{ Занесение в гистограмму }
end;
Rsr := SumR/Nizm;			{ Среднее }
Disp := (SumR2 - Nizm*sqr(Rsr))/(Nizm-1);			{ Дисперсия }
writeln (' Rсреднее = ',Rsr:5:2);
writeln (' Квадр. отклонение R = ',sqrt(Disp):5:2);
readln;	{ Ожидание <Enter> перед выводом гистограммы }
Gd := Detect; InitGraph(Gd, Gm, 'c:\tp\bgi');			{ Переход }
if GraphResult <> grOk then begin			{ в графический }
writeln (' Graph error or bgi driver not found ');			{ режим }

Halt;
end;
Gistogram(green);	{ Вывод гистограммы на экран }
readln;	{ Ожидание <Enter> после вывода гистограммы }
CloseGraph;
end.
В программе используется модуль Gisto с тремя процедурами для
работы с гистограммой:	InitGist − инициализация работы с гистограммой,

InGist − ввод текущего значения в массив гистограммы, Gistogram − вывод гистограммы на экран. Текст модуля должен находиться в файле Gisto.pas , а сам файл нужно поместить в текущую рабочую директорию (папку). Перед компиляцией программы файл Gisto.pas следует предварительно откомпилировать с помощью опции Alt-F9 , чтобы в рабочей директории появился файл Gisto.tpu , либо компиляцию основной программы нужно выполнять с помощью опций Build или Make из меню опции Compile ТурбоПаскаля. Текст модуля приведен ниже:

{Пакет процедур для построения гистограммы распределений }

{Файл: gisto.pas }

UNIT Gisto;
INTERFACE
uses Graph;
var
I, NGist : Integer;	{ NGist-число интервалов гистограммы }
OldPattern : FillPatternType;
Xstart,Xfin,deltaX : real;
MGist : array[1..580] of integer;	{ массив гистограммы }

procedure InitGist(Ng : integer; Xl,Xh : real); procedure InGist(Value : real);

procedure Gistogram(Color : Byte);

IMPLEMENTATION

{Процедура инициализации для построения гистограммы }

{Ng - число интервалов гистограммы;

Xl,Xh - начальное и конечное значение гистограммы по оси X }

procedure InitGist(Ng:integer; Xl,Xh:real); var

i : integer; begin

if Ng <= 580 then Ngist:=Ng else begin

writeln('Число интервалов гистограммы > 580 !');

Halt;
end;
for i := 1 to NGist do MGist[i] := 0;		{ очистка массива гистограммы }
Xstart := Xl;	{ начальное значение гистограммы по оси X }
Xfin:=Xh;	{ конечное значение гистограммы по оси X }
deltaX := (Xh-Xl) / NGist;	{ интервал построения гистограммы по оси X }
end;
{ Процедура занесения значения в массив гистограммы }
procedure InGist(Value : real);		{ Value - вносимое значение }
var
i : integer;
begin
i := trunc((Value - Xstart)/deltaX)+1;		{ номер элемента по x}
if i < 1 then i := 1;		{ защита от выхода }
if i > NGist then i := NGist;		{ за границы массива }
MGist[i] := MGist[i] + 1;		{ добавление точки в массив }
end;
{ Процедура вывода гистограммы на экран }
procedure Gistogram(Color : Byte);		{ Color - цвет вывода гистограммы }
const
MaxY = 420;	{ максимальный размер гистограммы по Y }
X0 = 50; Y0 = 450;	{ координаты начальной точки вывода }
var

max,x,y,i,shir : integer; mash : real;

s : string;

begin

{Определение максимума массива и масштаба по Y } max := MGist[1];

for i := 2 to NGist do

if MGist[i] > max then max := MGist[i];

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в папке Stohastic

#
18.08.2019908.97 Кб9stohastic.pdf
#
18.08.20195.54 Mб22Методичка_Стохастика_Федунов.doc