

p(x) такого распределения полагается равной 1 (b − a) , если a ≤ x ≤ b ,
(b − a) , если a ≤ x ≤ b ,
и равной 0 , если x не принадлежит сегменту [a, b] . Поскольку, за исключением очень специальных случаев, результаты статистического моделирования не зависят от того, определено ли равномерное распределение на интервале (a, b) или на сегменте [a, b] , мы будем здесь и в дальнейшем считать равномерное распределение определенным на
интервале |
(a, b) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
b + a |
|
|
|
Легко вычислить, что |
M{X} = ∫ x p(x) dx = |
, а |
|
||||||||||
|
|
||||||||||||
|
|
|
|
|
|
a |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
b |
|
|
|
b + a |
2 |
|
(b − a)2 |
|
|
D{X} = M{(X − M{X}) |
|
} = ∫ |
x |
− |
|
|
|
p(x) dx = |
|
. |
|||
|
2 |
12 |
|||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В частном случае, когда |
|
|
a = 0 |
|
и b = 1, |
имеем |
равномерно |
||||||
распределенную на интервале |
(0,1) случайную величину, |
играющую |
|||||||||||
значительную роль в методе Монте-Карло. |
Для таких величин |
|
|||||||||||
M{X} = 1 |
, а D{X} = |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
12 |
|
|
|
|
|
|
|
|
|
|
||
Пример 2. Нормальное (или гауссовское) распределение.
Нормальной |
(или |
гауссовской) называется случайная величина X , |
||||||
определенная на |
всей |
числовой |
оси |
(− ∞, ∞) и имеющая плотность |
||||
распределения вероятности |
|
|
|
|
||||
|
1 |
|
|
|
(x − a) |
2 |
|
|
p(x) = |
|
|
− |
|
|
|||
|
exp |
2σ |
2 |
|
, |
|||
|
2π σ |
|
|
|
|
|
||
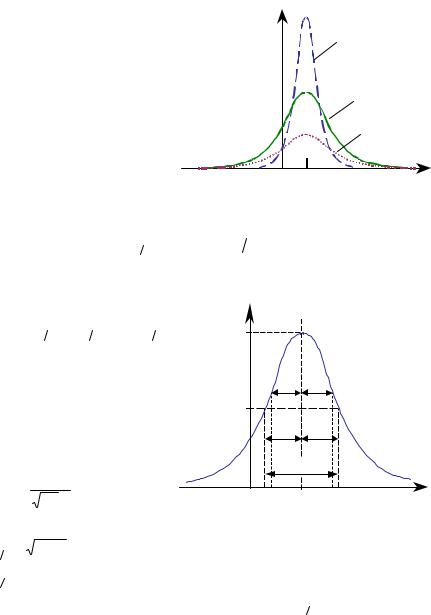
где a и σ − числовые параметры. Для гауссовского распределения имеем:
M{X } = a , D{X} = σ2 .
9
|
|
Величина |
a |
характери- |
|
p(x) |
|
|
|
|
||||||
зует |
|
центр |
тяжести |
распре- |
|
|
|
|
|
|||||||
|
|
|
|
|
σ = 0.5 |
|||||||||||
деления |
X |
и |
не |
влияет |
на |
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||||
форму кривой. Величина же σ |
|
|
|
|
|
|
||||||||||
характеризует разброс случай- |
|
|
|
|
|
σ = 1.0 |
||||||||||
ной величины |
X |
относитель- |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||
но ее среднего значения a . |
|
|
|
|
|
|
σ = 2.0 |
|||||||||
|
|
Последнее |
|
утверждение |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
можно выразить и по-другому. |
|
|
0 |
a |
|
x |
||||||||||
Характерный размер |
функции |
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||
по |
|
оси |
аргумента |
принято |
|
|
|
|
|
|
||||||
определять как ширину на полувысоте, т.е. за характерный размер |
||||||||||||||||
принимается |
ширина |
∆1 2 |
|
на уровне 1 2 от максимального значения |
||||||||||||
функции (см. рис.). |
Так как гауссовская функция симметрична относительно |
|||||||||||||||
вертикальной прямой, прохо- |
|
|
|
|
|
|
||||||||||
дящей через среднее значение |
|
p(x) |
|
|
|
|||||||||||
a , |
то ∆1 2 = 2w1 2 |
, |
где w1 2 |
|
pmax |
|
|
|
|
|||||||
− |
полуширина |
|
функции |
на |
|
|
|
|
|
|
||||||
полувысоте. |
Нетрудно вычис- |
0.607 pmax |
σ |
σ |
|
|
||||||||||
лить, |
что |
при |
|
x = a ± σ |
|
|
||||||||||
|
|
|
|
|
||||||||||||
значение |
функции |
равно |
0.5 pmax |
|
|
|
|
|||||||||
|
|
w1/2 |
w1/2 |
|
|
|||||||||||
p(a ± σ) = 0.607 |
|
|
от |
ее |
|
|
|
|
||||||||
максимального |
|
|
|
значения |
|
|
|
∆1/2 |
|
|
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
pmax |
= |
|
. |
|
|
|
|
|
0 |
|
a |
|
x |
|||
|
|
|
|
2π σ |
|
|
|
|
|
|
|
|
||||
Соответственно, |
полуширина |
|
|
|
|
|
|
|||||||||
w1 2 |
|
= |
2 ln 2 σ ≈ 1.18 σ |
и |
полная |
ширина |
функции |
на |
полувысоте |
|||||||
∆1 2 |
≈ 2.36 σ . |
Видно, что полуширина функции на уровне |
p(a ± σ) лишь |
|||||||||||||
немного (на 18 % ) отличается от полуширины w1 2 , определенной на полувысоте. Поэтому для гауссоподобных функций за полуширину обычно
10

принимают величину σ , а за полную ширину функции − величину |
2σ |
|||||
вместо ∆1 2 . Таким |
образом, |
величина σ |
является характерной |
|||
полушириной гауссовской функции плотности вероятности. |
|
|
||||
|
|
a+3σ |
|
|
|
|
Можно вычислить, |
что |
∫p(x) dx = 0.997 , |
или, что то же самое, |
|||
|
|
a−3σ |
|
|
|
|
P(a − 3σ < X < a + 3σ) = 0.997 . |
Практически |
это |
означает, |
что |
||
вероятность получения |
значения |
X , отличающегося |
по абсолютной |
|||
величине больше чем на |
3σ от среднего значения a , очень мала (≈0.3 %). |
||||||||
Заметим, что все нормальные распределения с параметрами (a,σ) |
могут |
||||||||
быть сведены к |
одному |
|
нормальному распределению величины |
U с |
|||||
параметрами |
|
(0,1) , |
|
|
называемому |
стандартным нормальным |
|||
распределением и имеющему плотность вероятности |
|
||||||||
|
1 |
|
u |
2 |
|
|
|
|
|
p(u) = |
|
|
|
. |
|
|
|||
|
exp − |
|
|
|
|
|
|
||
|
2π |
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|||
Стандартное нормальное распределение легко получается из |
|||||||||
нормального распределения с параметрами |
(a, σ) путем замены переменной |
||||||||
U = (X − a) / σ . |
Любая же нормально распределенная случайная величина |
||||||||
X с параметрами (a, σ) |
|
может быть получена из стандартной нормальной |
|||||||
величины U с параметрами (0,1) преобразованием |
|
||||||||
X = a + U σ .
Распределение Гаусса − одно из самых распространенных в физике. Такому распределению подчиняются ошибки измерения физических величин, результаты стрельбы по мишени, распределение проекций скоростей молекул газа (распределение Максвелла), вероятность малых флуктуаций и многое другое.
11
ОСНОВНЫЕ ПРИНЦИПЫ МЕТОДА СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Сущность метода статистического моделирования заключается в следующем. Выбирается определенная модель, описывающая исследуемый процесс, явление, систему. На основании математического описания модели и численных методов разрабатывается моделирующий алгоритм, имитирующий внешние воздействия на систему, поведение ее элементов, их взаимодействие и последовательное изменение состояний всей системы во времени.
Затем осуществляется одна случайная реализация моделируемого явления, например: один "распад" радиоактивного атома, один "процесс" прохождения элементарной частицы через вещество, один "обстрел" цели, один "день работы" транспорта, и т.п..
После осуществления единичной реализации моделируемого явления эксперимент многократно повторяется, и по результатам моделирования определяются различные характеристики модели. При этом полнота и достоверность полученной путем моделирования информации о свойственных системе закономерностях зависят от того, насколько точно использованная математическая модель описывает реальную систему, от точности вычислительных методов, использованных при разработке моделирующего алгоритма, и от числа проведенных испытаний.
Продемонстрируем эти принципы на простом примере. Пусть необходимо
определить |
площадь |
произвольной |
||
плоской фигуры |
S . |
|
|
|
Ограничим |
фигуру |
квадратом |
со |
|
стороной a |
и выберем в квадрате |
N |
||
случайных точек. Пусть N ′ − число |
||||
точек, попавших внутрь фигуры |
S . |
|||
Тогда геометрически |
очевидно, |
что |
||
y a 





 S
S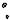

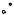

x
0 |
a |
12
площадь фигуры S приближенно равна a 2 N ' / N . Причем, чем больше будет значение N , тем точнее будет оценка площади фигуры S . Отсюда ясно, как можно построить алгоритм для вычисления площади такой фигуры:
1. Разыгрываем случайную величину |
ξ , равномерно распределенную на |
интервале (0, a) . Значение ξ |
будет означать X - координату |
случайной точки.
2.Разыгрываем случайную величину χ , равномерно распределенную на
интервале (0, a) . Значение χ будет означать Y - координату случайной точки.
3.Проверяем, попала ли разыгранная точка (ξ,χ) внутрь фигуры S .
Если попала, то добавляем к счетчику N ′ единицу (перед началом описываемых действий счетчик N ′ должен быть обнулен).
4.Повторяем предыдущий процесс (пункты 1,2,3) N раз.
5.Вычисляем значение интеграла.
Отметим две особенности метода статистического моделирования. Первая − относительная простота вычислительного алгоритма. Как правило, составляется программа для прослеживания одной реализации, а затем эта процедура N раз повторяется. Вторая − погрешности вычислений обычно
пропорциональны 1  N , т.е. метод нецелесообразно применять там, где требуется очень высокая точность вычислений.
N , т.е. метод нецелесообразно применять там, где требуется очень высокая точность вычислений.
Таким образом, единичная реализация является основным элементом метода статистического моделирования и представляет один случай осуществления моделируемого процесса (явления) со всеми присущими ему случайностями. Каждый раз, когда в ход моделируемого процесса вмешивается случайность, должен быть реализован какой-то механизм случайного выбора (бросание монет, костей, вынимание жетона из вращающегося барабана, числа из набора чисел, и т.д.), называемый "единичным жребием".
13
Единичный жребий должен давать ответ на один из вопросов:
произошло или не произошло некое событие A ? |
какое из возможных |
||||
событий |
A1, A2 ,..., Ak |
произошло ? |
какое значение приняла случайная |
||
величина |
X ? |
какую совокупность значений приняла система случайных |
|||
величин |
X1 , |
X 2 ,..., |
X k ? и т.п.. |
Например, |
при моделировании |
прохождения элементарной частицы через вещество единичный жребий должен отвечать на вопросы: произошло или не произошло взаимодействие частицы с веществом (событие A ) ? какой процесс произошел при взаимодействии − поглощение или рассеяние (события A1, A2 ,..., Ak ) ? если произошло рассеяние, то на какой угол частица рассеялась (случайная
величина |
X ) ? каковы |
координаты |
точки взаимодействия частицы с |
|
веществом (система случайных величин |
X1 , X 2 ,..., |
X k ) ? и т.д.. |
||
Каждая |
реализация |
случайного |
явления |
методом Монте-Карло |
рассматривается как последовательность конечного числа элементарных случайных событий (единичных жребиев), перемежающихся обычными расчетами. Расчетами учитывается влияние исхода единичного жребия на ход моделирования (в частности, на условия, в которых будет осуществляться следующий единичный жребий).
Для того, чтобы реализовать единичный жребий, необходимо получать на ЭВМ последовательности значений случайных величин (скалярных или векторных) с заданными законами распределения. Поскольку при решении конкретных задач могут потребоваться случайные величины с самыми разнообразными распределениями (пуассоновское, гауссовское, биноминальное, равномерное, экспоненциальное и т.д.), то задача моделирования необходимой случайной величины может показаться неимоверно сложной. Однако, все эти задачи могут быть разрешены с помощью одного стандартного механизма, позволяющего решить одну единственную задачу − получить случайную величину, распределенную с равномерной плотностью от 0 до 1. Тогда, как показано ниже, случайную величину y с произвольной плотностью распределения f ( y) можно найти с помощью преобразований одного или нескольких независимых значений случайной величины γ , равномерно распределенной в интервале (0,1).
14
ПОЛУЧЕНИЕ РАВНОМЕРНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ЧИСЕЛ
Как упомянуто выше, ключевой проблемой статистического
моделирования |
является получение |
случайных |
чисел |
γ , равномерно |
распределенных |
в интервале (0,1). |
Отметим |
три |
основных способа |
получения γ : табличный, аппаратный и алгоритмический. Первый способ заключается в использовании специально составленных таблиц случайных чисел. Таблицы, полученные с помощью специальных приборов (типа рулетки), заносятся в память ЭВМ и используются по мере необходимости. Основной недостаток − необходимость в памяти достаточно большой емкости, затрудняющий решение "больших" задач, тем более, что преимущество "случайных" таблиц перед "псевдослучайными" числами, получаемыми алгоритмически, никем не было доказано. Во втором способе используются аппаратные датчики, основанные на некоторых физических процессах, случайных по своей природе (шумы в электронных и полупроводниковых приборах, процессы при радиоактивном распаде и т.п.). Основные недостатки − невозможность повторного получения одной и той же последовательности случайных величин для проверочных расчетов и невозможность гарантировать постоянную надежную работу датчика.
Как правило, случайные числа γ получают в настоящее время на ЭВМ программным способом, производящим последовательности "псевдослучайных" чисел. Для этого используются рекуррентные формулы, когда каждое последующее число γi+1 образуется из предыдущего γi на основании применения некоторого алгоритма. Подобная последовательность чисел, не будучи истинно случайной по своей природе, обладает свойствами, аналогичными свойствам случайных величин. Большинство алгоритмов получения псевдослучайных чисел основано на том, что при перемножении двух многоразрядных чисел x и y средние разряды произведения xy являются сложной функцией сомножителей и обладают "случайными" свойствами.
15
Простой пример получения равномерно распределенной в интервале (0,1) случайной величины ξ может быть осуществлен следующим алгоритмом:
ξi+1 = {π ξi } , ξ0 = 0.1 .
Знак { } означает, что берется дробная часть произведения. Вычисления дают такую последовательность: ξ0 = 0.1, ξ1 = 0.415926 , ξ2 = 0.667 ,
ξ3 = 0.54422 , ξ4 = 0.97175, ξ5 = 0.28426 и т.д..
Кнастоящему времени разработано множество алгоритмов получения псевдослучайных чисел. Наиболее популярным для получения
псевдослучайных чисел ξ1, ξ2 ,..., является метод вычетов (мультипликативный датчик), который можно записать в следующей форме:
ξi+1 = {M ξi } , ξ0 = 2−m ,
где M − достаточно большое целое число, фигурные скобки обозначают дробную часть, а m − число двоичных разрядов в мантиссе чисел в ЭВМ. Методы выбора значений M , ξ0 и m разнятся для разных вариантов реализаций данного метода (это своя собственная "наука") и определяют основные свойства датчика случайных чисел (соответствие статистическим критериям, длину периода повторения последовательности и т.п.).
В составе математического обеспечения системы Turbo Pascal также имеется датчик псевдослучайных чисел − функция Random() . Если эта функция используется без параметра, то ее значением будет равномерно распределенное реальное число в интервале от 0 до 1. Если же она вызывается с параметром (целым числом n ), то результатом будет равномерно распределенное целое число в интервале от 0 до n . Вызов функции в программе осуществляется следующим образом:
16
x := Random; |
{ |
0 |
< x < 1 |
} |
или |
|
|
|
|
m := Random(n); |
{ |
0 |
≤ m < n |
} . |
Поскольку получение псевдослучайных чисел осуществляется по рекуррентной формуле, то при запуске программы функция Random будет
всегда |
начинать последовательность |
с одного |
и того же первого |
числа |
(аналог |
ξ0 в приведенных выше |
примерах). |
Это означает, что после |
|
компиляции и запуска программы вы все время будете получать одну и ту же наперед заданную последовательность чисел. С одной стороны, это иногда удобно для отладки программы, а, с другой стороны, может мешать при моделировании. Чтобы исключить такую ситуацию, существует специальная процедура Randomize , которая инициализирует случайным значением (текущим системным временем) генератор псевдослучайных чисел, используемый функцией Random . Таким образом, обращение к процедуре Randomize позволяет смоделировать начальную "случайность" программного датчика псевдослучайных чисел.
МОДЕЛИРОВАНИЕ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Рассмотрим дискретную случайную величину ξ , принимающую n
значений |
X1, X 2 , ..., |
X n |
с вероятностями P1, P2 ,..., Pn . Эта величина |
||||||
задается таблицей распределения |
|
||||||||
X |
|
X |
|
... X |
|
|
n |
=1 . |
|
|
|
, |
P |
||||||
ξ = |
|
1 |
P |
2 |
... P |
n |
|||
|
P |
|
|
|
∑ k |
||||
|
1 |
2 |
n |
|
k =1 |
|
|||
Для моделирования такой дискретной случайной величины разбивают отрезок [0,1] на n последовательных отрезков ∆1, ∆2 ,..., ∆n , длины которых равны соответствующим вероятностям P1, P2 ,..., Pn . Получают
17
случайную величину |
γ |
, равномерно распределенную в интервале (0,1), и |
||||||||||
полагают |
ξ = X k |
, если |
γ ∆k . |
|
|
|
|
|
|
|||
Аналогичным образом осуществляется моделирование случайных |
||||||||||||
событий. |
Пусть необходимо смоделировать реализацию (осуществление или |
|||||||||||
неосуществление) какого-либо события |
Sk из ряда событий |
|
|
S1 , S2 ,..., Sn , |
||||||||
образующих полную группу событий. |
Свяжем с этой системой событий |
|||||||||||
случайную величину |
ξ , равную номеру события: |
|
|
|
|
|
||||||
|
1 |
2 ... |
n |
, где P − вероятность наступления |
S |
|
. |
|
||||
ξ = |
|
|
|
|
|
|
||||||
P P ... P |
|
k |
|
|
|
k |
|
|
||||
|
1 |
2 |
|
n |
|
|
|
|
|
|
|
|
Тогда полагаем, |
что произошло случайное событие Sk |
, |
если случайная |
|||||||||
величина |
ξ |
приняла значение, равное |
k . |
|
|
|
|
|
||||
Среди дискретных случайных величин важное значение имеют |
||||||||||||
целочисленные случайные величины с распределением вида |
|
|
pk |
= P(ξ = k) |
||||||||
( k = 0,1, 2,... ), |
которые |
связаны простыми рекуррентными |
формулами |
|||||||||
pk +1 = pk r(k) . |
Среди таких распределений наиболее важными и часто |
|||||||||||
используемыми являются биноминальное распределение и распределение Пуассона. Для биноминального распределения с параметрами ( p, n) имеем:
P = P(ξ = k) |
= Ck pk (1− p)n−k |
||||||
k |
|
|
|
n |
|
|
|
r(k) = |
pk +1 |
= |
n − k |
|
p |
, |
|
|
k +1 |
1− p |
|||||
|
pk |
|
|
|
|||
, k = 0,1,..., n |
, |
|
|
||
Cnk = |
n! |
|
|
. |
|
(n − k)!k! |
|||||
|
|
||||
Для распределения Пуассона с параметром λ имеем:
pk = |
λk |
e−λ |
, |
r(k) = |
λ |
|
, k = 0,1, . |
|
k! |
k +1 |
|||||||
|
|
|
|
|
||||
18
