Центральные композиционные планы
Разработка
математической модели предусматривает
принцип «от простого к более сложному»,
то есть постепенный переход от «грубой»
модели к моделям, более точно описывающим
исследуемый процесс. В имитационной
модели, соответствующей полиному первого
порядка, этот принцип предусматривает
переход к полиному второго порядка. Как
было показано ранее, шаговое движение
к экстремуму продолжается до тех пор,
пока исследователь не достигнет области,
близкой к экстремуму (или «почти
стационарной»), которая не может быть
описана линейным приближением. Здесь
уже становятся значимыми квадратичные
эффекты. Близость к «почти стационарной»
области можно установить, поставив ряд
экспериментов в центре плана, определить
среднее значение функции отклика
и сравнить его с теоретическим значением
a0,
исходя из предполагаемой имитационной
модели в виде полинома первого порядка.
Вычисляемое
для линейного уравнения значение a0
при реализации ПФЭ или ДФЭ в «почти
стационарной» области является совместной
оценкой для свободного члена и суммы
квадратичных членов, так как безразмерные
значения, стоящие в соответствующих
столбцах матрицы, будут одинаковыми.
Поэтому разность
может дать представление о кривизне
поверхности отклика. «Почти стационарную»
область обычно удается описать с
достаточной точностью полиномом второго
порядка.
В то же время, из теории интерполяции известно, что для нахождения раздельных оценок коэффициентов интерполяционного полинома число уровней изменения каждой из независимых переменных должно быть на единицу больше порядка полинома. Иными словами, для вычисления полинома второго порядка число уровней должно быть, как минимум, три. В ПФЭ 3k при k=2 потребуется проведение минимум девяти опытов, а для трех факторов, их число резко возрастет до 27. Поэтому при увеличении числа учитываемых факторов применение ПФЭ 3k не рационально, так как это планирование характеризуется резким увеличением объема эксперимента.
С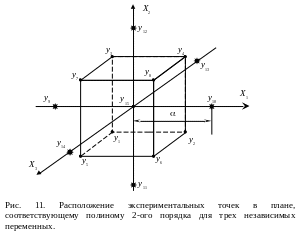
ократить
число опытов можно, используя так
называемые центральные композиционные
планы (ЦКП), ядром которых являются
линейные ортогональные планы. Большое
преимущество этих планов состоит в том,
если гипотеза о линейности математической
модели, соответствующей исследуемому
процессу, в результате анализа
экспериментальных данных не подтвердилась,
то нет необходимости ставить все
эксперименты заново для получения
модели более высокого порядка. Достаточно,
в этом случае, добавить несколько
специально спланированных экспериментальных
точек, чтобы получить план, соответствующий
полиному второго порядка.
Построение ЦКП можно пояснить на примере с тремя независимыми переменными, соответствующие трем факторам X1, X2 и X3. Предположим, что для нахождения линейной модели применен ПФЭ 23, экспериментальные точки которого находятся в вершинах куба (рис. 11). В результате анализа экспериментальных данных установлено, что имитационная математическая модель в виде полинома первого порядка не адекватна исследуемому процессу.
Тогда в центре плана, соответствующего начальному значению всех учитываемых в эксперименте факторов, проводится опыт, условия которого в матрице планирования эксперимента отображаются нулями для безразмерных величин всех факторов.
Для повышения достоверности полученного экспериментального значения функции отклика у0 в центре плана, опыты повторяют при неизменных нулевых значениях факторов. Подсчитанное среднее значение функции отклика у0 сравнивают с теоретическим значением a0, которое несложно получить из разработанной линейной модели процесса в результате ранее проведенного ПФЭ 23 и анализа его результатов.
По разности a0 - у0 оценивают кривизну поверхности отклика. При подтверждении неадекватности линейной модели ставятся дополнительные опыты для значений факторов, превышающих их абсолютные значения по верхнему и нижнему уровням (в безразмерных величинах). Эти значения должны быть больше единицы по абсолютным значениям, установленным в предшествующем плане ПФЭ.
Таким образом, в ПФЭ 23, к ранее проведенным восьми опытам добавляются еще семь опытов (включая опыт в центре плана), шесть из которых соответствуют «звездным точкам». «Звездные точки» (рис. 11) представляют собой два уровня варьирования каждым из трех факторов, значения которых лежат за пределами граней куба.
Как видно из рис. 11, все «звездные точки» расположены на расстоянии большем, чем ±1 от центра плана и лежат на поверхности сферы диаметром 2α.
Общее число опытов центрального композиционного плана при k факторах составит
где 2k - число «звездных точек»; т0 - число опытов в центре плана, а общее число уровней варьирования ЦКП равно пяти.
В теории планирования экспериментов для получения моделей 2-го порядка различают несколько типов ЦКП. Наибольшее распространение получили ортогональный и рототабельный ЦКП.
Центральный композиционный ортогональный план (ЦКОП).
При составлении матрицы планирования эксперимента этот план предусматривает проведение только одного опыта, условия которого соответствуют начальным значениям всех учитываемых факторов (в центре плана), т. е. т0 = 1. Поэтому для ЦКОП число опытов равно
Соответствующая матрица ЦКОП для имитационной модели исследуемого процесса, соответствующая полиному 2-го порядка при k = 3, приведена в табл. 2. Как видно из таблицы, ЦКОП при k = 3 содержит всего 15 опытов, в то время как ПФЭ 33 потребовал бы проведения 27 опытов. Следует также обратить внимание на то, что условие ортогональности матрицы выполняется только для линейных членов соответствующего полинома 2-го порядка, представляющего собой имитационную модель вида
|
(**) |
Таблица 2 |
||||||||||||
Матрица центрального композиционного ортогонального плана |
||||||||||||
Номер опыта |
x0 |
x1 |
x2 |
x3 |
x1 x2 |
x1 x3 |
x2 x3 |
x1 x2 x3 |
|
|
|
y |
1 |
+1 |
–1 |
–1 |
–1 |
+1 |
+1 |
+1 |
–1 |
+1 |
+1 |
+1 |
y1 |
2 |
+1 |
+1 |
–1 |
–1 |
–1 |
–1 |
+1 |
+1 |
+1 |
+1 |
+1 |
y2 |
3 |
+1 |
–1 |
+1 |
–1 |
–1 |
+1 |
–1 |
+1 |
+1 |
+1 |
+1 |
y3 |
4 |
+1 |
+1 |
+1 |
–1 |
+1 |
–1 |
–1 |
–1 |
+1 |
+1 |
+1 |
y4 |
5 |
+1 |
–1 |
–1 |
+1 |
+1 |
–1 |
–1 |
+1 |
+1 |
+1 |
+1 |
y5 |
6 |
+1 |
+1 |
–1 |
+1 |
–1 |
+1 |
–1 |
–1 |
+1 |
+1 |
+1 |
y6 |
7 |
+1 |
–1 |
+1 |
+1 |
–1 |
–1 |
+1 |
–1 |
+1 |
+1 |
+1 |
y7 |
8 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
y8 |
9 |
+1 |
– |
0 |
0 |
0 |
0 |
0 |
0 |
+ |
0 |
0 |
y9 |
10 |
+1 |
+ |
0 |
0 |
0 |
0 |
0 |
0 |
+ |
0 |
0 |
y10 |
11 |
+1 |
0 |
– |
0 |
0 |
0 |
0 |
0 |
0 |
+ |
0 |
y11 |
12 |
+1 |
0 |
+ |
0 |
0 |
0 |
0 |
0 |
0 |
+ |
0 |
y12 |
13 |
+1 |
0 |
0 |
– |
0 |
0 |
0 |
0 |
0 |
0 |
+ |
y13 |
14 |
+1 |
0 |
0 |
+ |
0 |
0 |
0 |
0 |
0 |
0 |
+ |
y14 |
15 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
y15 |
Из анализа табл. 2 нетрудно убедиться, что для матрицы ЦКОП условие ортогональности не выполняется для столбцов, соответствующих квадратичным членам полинома, так как
где i,l = 1 .. k; x2ij - безразмерное квадратичное значение i-го фактора, соответствующее j-му опыту.
Для приведения матрицы (табл. 2) к ортогональному виду необходимо провести преобразование квадратичных переменных
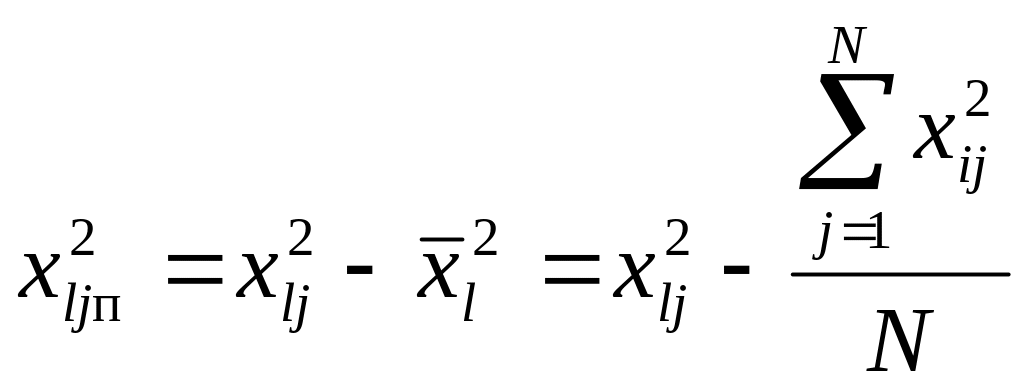
где x2ijп – преобразованное (п), безразмерное квадратичное значение i-го фактора, соответствующее j-му опыту.
Для выполнения условия ортогональности матрицы ЦКОП, помимо преобразования столбцов, соответствующих квадратичным членам полинома, и приведения значений, стоящих в них, необходимо величину звездного плеча α выбирать соответственно:
при k<5
при k=5
Ядро ЦКОП при k<5 составляет, как правило, ПФЭ типа 2k, а при k≥5 - ДФЭ типа 2k-1, так как во втором случае полуреплика от ПФЭ вполне обеспечивает возможность независимой оценки линейных членов полинома и членов, учитывающих эффект взаимодействия факторов.
Значения звездного плеча, согласно условиям приведенным выше, равны
K |
2 |
3 |
4 |
5 |
6 |
7 |
Α |
1,00 |
1,215 |
1,414 |
1,547 |
1,724 |
1,885 |
Преобразовав соответствующим образом матрицу ЦКОП, приведенную в табл. 1, получим матрицу ЦКОП, которая полностью соответствует условию ортогональности (табл. 3).
Для приведенной в табл. 3 матрицы ЦКОП будет соответствовать имитационная модель
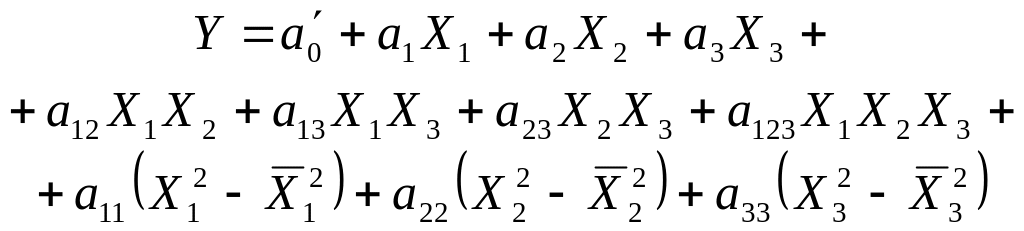
Для перехода от данной модели к модели (**), необходимо пересчитать коэффициент a0, который будет определяться
или, в общем виде
Таблица 3 |
||||||||||||
Преобразованная матрица ЦКОП, отвечающая требованиям ортогональности |
||||||||||||
Номер опыта |
x0 |
x1 |
x2 |
x3 |
x1 x2 |
x1 x3 |
x2 x3 |
x1 x2 x3 |
|
|
|
y |
1 |
+1 |
–1 |
–1 |
–1 |
+1 |
+1 |
+1 |
–1 |
0,27 |
0,27 |
0,27 |
y1 |
2 |
+1 |
+1 |
–1 |
–1 |
–1 |
–1 |
+1 |
+1 |
0,27 |
0,27 |
0,27 |
y2 |
3 |
+1 |
–1 |
+1 |
–1 |
–1 |
+1 |
–1 |
+1 |
0,27 |
0,27 |
0,27 |
y3 |
4 |
+1 |
+1 |
+1 |
–1 |
+1 |
–1 |
–1 |
–1 |
0,27 |
0,27 |
0,27 |
y4 |
5 |
+1 |
–1 |
–1 |
+1 |
+1 |
–1 |
–1 |
+1 |
0,27 |
0,27 |
0,27 |
y5 |
6 |
+1 |
+1 |
–1 |
+1 |
–1 |
+1 |
–1 |
–1 |
0,27 |
0,27 |
0,27 |
y6 |
7 |
+1 |
–1 |
+1 |
+1 |
–1 |
–1 |
+1 |
–1 |
0,27 |
0,27 |
0,27 |
y7 |
8 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
0,27 |
0,27 |
0,27 |
y8 |
9 |
+1 |
– |
0 |
0 |
0 |
0 |
0 |
0 |
+0 |
-0 |
-0 |
y9 |
10 |
+1 |
+ |
0 |
0 |
0 |
0 |
0 |
0 |
+0 |
-0 |
-0 |
y10 |
11 |
+1 |
0 |
– |
0 |
0 |
0 |
0 |
0 |
-0 |
+0 |
-0 |
y11 |
12 |
+1 |
0 |
+ |
0 |
0 |
0 |
0 |
0 |
-0 |
+0 |
-0 |
y12 |
13 |
+1 |
0 |
0 |
– |
0 |
0 |
0 |
0 |
-0 |
-0 |
+0 |
y13 |
14 |
+1 |
0 |
0 |
+ |
0 |
0 |
0 |
0 |
-0 |
-0 |
+0 |
y14 |
15 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-0 |
-0 |
-0 |
y15 |
При применении ЦКОП получение идентичной информации во всех направлениях исследуемого пространства невозможно, так как дисперсии ошибок определения коэффициентов полинома различны, т. е. точность предсказания выходной величины (значения функции отклика Y) в различных направлениях факторного пространства неодинакова – информационные поверхности не являются сферами. Это можно пояснить с помощью рис. 12.
Ранее было показано, что точность получаемого экспериментально представления об исследуемом объекте зависит от интервалов варьирования. При расположении экспериментальных точек как предусмотрено опытами в ЦКОП на рис. 12, а) и б) точность информации, получаемой с различных направлений, меняется при повороте осей координат относительно экспериментальных точек. Так, на рис. 12, б) более точную информацию (экспериментальные точки расположены на большем расстоянии друг от друга) имеем по осям координат, а на рис. 12, а) – с межосевых направлений, но в обоих случаях информационные поверхности далеки от сферических.
Центральный композиционный рототабельный план (ЦКРП).
Более удачным является рототабельное планирование эксперимента, при котором информационная поверхность приближается к сферической т. е. точность Y во всех направлениях на одинаковом расстоянии R от центра планирования становится практически одинаковой.
При этом, ЦКРП позволяет минимизировать ошибки в определении Y, связанные с неадекватностью представления результатов исследования процесса имитационной моделью в виде полинома 2-го порядка. Это достигается тем, что, выбирая удаленные от центра плана «звездные точки» на осях координат для непрерывности информационной поверхности, они дополняются информацией из центра плана, представляющей собой сферу с нулевым радиусом, т. е. информацией равноточной во всех направлениях. Удельный вес этой информации в общем объеме информации увеличивается, что достигается увеличением числа опытов (т0) в центре плана. Роль центральных точек можно образно сравнить с ролью «золотого петушка» в одноименной сказке А. С. Пушкина, который находясь на шпиле дворца давал равноточную информацию о приближающемся противнике со всех направлений. Ставя несколько экспериментов в центре плана, «накачиваем» информацию в центр плана, приближая информационные поверхности к сферам.
Таким образом, в ЦКРП, число опытов т0 в центре плана зависит от числа учитываемых в эксперименте факторов, т. е. т0=f(k). Так, для k=3, т0=6 (т. е. числу звездных точек). Это безусловно приводит к увеличению числа номеров опытов по сравнению с ЦКОП, но обеспечивает непрерывность информационной поверхности и ее идентичность независимо от поворота осей координат.
При реализации рототабельных планов можно отказаться от постановки параллельных опытов для оценки воспроизводимости экспериментов, что уменьшит общее число опытов по сравнению с ЦКОП. Дисперсия воспроизводимости (дисперсия экспериментальных значений функции отклика в параллельных опытах) может быть оценена в этом случае по экспериментам в центре плана.
Чтобы композиционный план был рототабельным, величина звездного плеча а выбирается из условий:
Подсчитанные значения звездного плеча α и число центральных точек т0, в зависимости от числа учитываемых в эксперименте факторов, приведены ниже.
k |
2 |
3 |
4 |
5 |
6 |
7 |
α |
1,414 |
1,682 |
2,00 |
2,00 |
2.38 |
2,83 |
т0 |
5 |
6 |
7 |
6 |
9 |
14 |
Для k=3 и соответственно т0=6 выражение для количества опытов примет вид
Из выражения следует, что для трех учитываемых в эксперименте факторов Х1, Х2 и Х3 в ЦКРП потребуется проведение не менее 20 опытов по сравнению с 15-ю опытами в случае применения ЦКОП (табл. 4). Причем, все эти дополнительные пять опытов проводятся в центре плана, т. е. для безразмерных значений всех факторов, равных нулю (Хi = 0).
Таблица 4 |
||||||||
Матрица центрального композиционного рототабельного плана |
||||||||
Номер опыта |
x0 |
x1 |
x2 |
x3 |
|
|
|
Y |
1 |
+1 |
–1 |
–1 |
–1 |
+1 |
+1 |
+1 |
y1 |
2 |
+1 |
+1 |
–1 |
–1 |
+1 |
+1 |
+1 |
y2 |
3 |
+1 |
–1 |
+1 |
–1 |
+1 |
+1 |
+1 |
y3 |
4 |
+1 |
+1 |
+1 |
–1 |
+1 |
+1 |
+1 |
y4 |
5 |
+1 |
–1 |
–1 |
+1 |
+1 |
+1 |
+1 |
y5 |
6 |
+1 |
+1 |
–1 |
+1 |
+1 |
+1 |
+1 |
y6 |
7 |
+1 |
–1 |
+1 |
+1 |
+1 |
+1 |
+1 |
y7 |
8 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
y8 |
9 |
+1 |
– α |
0 |
0 |
α2 |
0 |
0 |
y9 |
10 |
+1 |
+ α |
0 |
0 |
α2 |
0 |
0 |
y10 |
11 |
+1 |
0 |
– α |
0 |
0 |
α2 |
0 |
y11 |
12 |
+1 |
0 |
+ α |
0 |
0 |
α2 |
0 |
y12 |
13 |
+1 |
0 |
0 |
– α |
0 |
0 |
α2 |
y13 |
14 |
+1 |
0 |
0 |
+ α |
0 |
0 |
α2 |
y14 |
15 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
y15 |
16 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
y16 |
17 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
y17 |
18 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
y18 |
19 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
y19 |
20 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
y20 |
Столбцы, соответствующие взаимодействию линейных факторов в матрице ЦКРП отсутствуют. Из сравнения табл. 4 с табл. 2 и табл. 1 (матрица для ПФЭ типа 23) нетрудно убедиться в том, что значения, приведенные в этих столбцах включительно до опыта № 8, были бы идентичны. Начиная с опыта № 9, значения, соответствующие взаимодействию линейных факторов, будут равны нулю, т. е. не влияют на оценку значимости соответствующего коэффициента в полиноме при последующем анализе экспериментальных данных. Учитывая также тот факт, что оценка значимости этих коэффициентов, сделанная при обработке и анализе результатов эксперимента в процессе ранее проводимого ПФЭ, останется неизменной и в ЦКРП, приводить эти столбцы в матрице планирования ЦКРП не обязательно.
Из анализа табл. 4 видно, что матрица ЦКРП не соответствует условиям ортогональности для столбцов с квадратичными членами полинома. Поэтому оценка коэффициентов полинома 2-го порядка, проводимая по результатам эксперимента в соответствии с матрицей ЦКРП, не будет являться независимой. Но этот недостаток ЦКРП компенсируется более высокой точностью определения Y во всех направлениях на одинаковом расстоянии R от центра плана. При этом следует учитывать тот факт, что ЦКРП использует независимую оценку коэффициентов полинома при линейных его членах, проведенную по результатам предыдущего полного или дробного факторного эксперимента.