2.8. Непрерывность функции в точке. Односторонняя непрерывность

Определение 2.14.

Пусть функция f(x) определена в некоторой окрестности точки . Функция f(x) называется непрерывной в точке , если .

В этом определении заключены три требования: 1) функция f(x) определена в точке ; 2) существует ; 3) справедливо равенство .

Определение 2.15.

Пусть функция f(x) определена в некоторой левой полуокрестности точки . Функция f(x) называется непрерывной слева в точке , если .

Аналогично определяется непрерывность справа функции f(x) в точке .

Теорема 2.12.

Для того, чтобы функция f(x) была непрерывной в точке , необходимо и достаточно, чтобы она была в этой точке непрерывна и слева, и справа.

Пример 2.20.

Р

у

ассмотрим функцию f(x) = [x]. Такая функция называется целой частью числа. Каждому числу x она сопоставляет ближайшее целое число, меньшее или равное x.

2

1

3

2

1

-3

-2

-1

-1

х

-3

-2

Рис. 2.5.

В точках, соответствующих целым числам, эта функция непрерывна только справа. В остальных точках, как видно из рис. 2.5, исходная функция непрерывна.

Теорема 2.13. (об арифметических свойствах непрерывных функций).

Если функции f(x) и g(x) непрерывны в точке , то функции f(x) + g(x), f(x)g(x), также непрерывны в этой точке.

Теорема 2.14. (о непрерывности сложной функции).

Пусть функция u = g(x) непрерывна в точке , а функция y = f(u) непрерывна

в точке , причем = g( ), тогда сложная функция y = f(g(x)) непрерывна в точке .

Теорема 2.15. (о непрерывности элементарных функций).

Каждая элементарная функция непрерывна в любой точке из своей области определения, причем в граничных точках (если таковые имеются) она непрерывна слева или справа.

Замечание 2.8.

Непрерывность функций используется при вычислении пределов. Так, если функция f(x) непрерывна в точке , то , то есть задача отыскания предела свелась к вычислению значения функции в точке .

При вычислении пределов сложных функций в случае их непрерывности можно переставить местами операции взятия предела и непрерывной функции.

Пример 2.21.

.

Пример 2.22.

Вычислим предел показателя степени, используя эквивалентные замены:

.

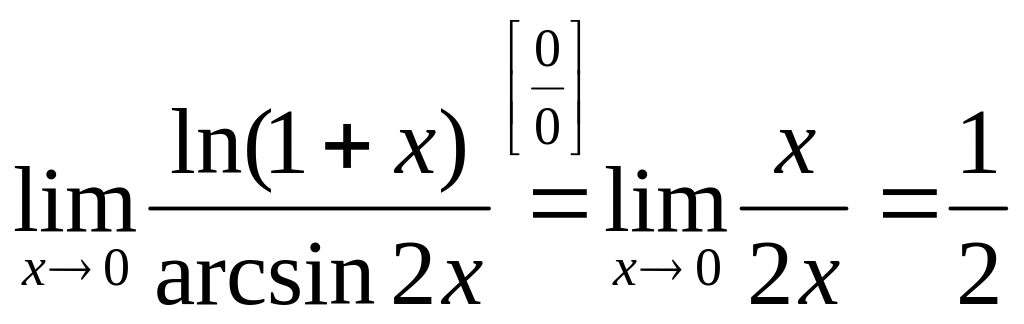Таким образом, .

2.9. Непрерывность функции на промежутке. Точки разрыва функции и их классификация

Определение 2.16.

1. Функция f(x) называется непрерывной на интервале (a,b), если она непрерывна в любой его точке.

2. Функция f(x) называется непрерывной на отрезке [а,b], если она непрерывна на интервале (a,b), а также непрерывна справа в точке a и слева в точке b.

Определение 2.17.

Пусть функция f(x) задана на некотором множестве X /R и для любого x X имеет место неравенство f(x) ≥ f(x₁), где x₁ X.

Тогда число f(x₁) называется наименьшим значением функции f(x) на множестве X.

Если же вычисляется неравенство f(x) ≤ f(x₂), где x₂ X, то число f(x₂) называется наибольшим значением функции f(x) на множестве X.

Теорема 2.16. (теорема Вейерштрасса).

Если функция f(x) непрерывна на отрезке [a,b] , то она ограничена на нем и среди ее значений существуют наименьшее m и наибольшее M.

Рис. 2.6.

Определение 2.18.

Пусть функция f(x) определена в некоторой окрестности точки x₀ за исключением возможно самой точки x₀.

Точка x₀ называется точкой разрыва функции f(x), если в этой точке функция либо не определена, либо не является непрерывной.

Определение 2.19.

Пусть точка x₀ есть точка разрыва функции f(x).

Если существуют конечные односторонние пределы , то x₀ называется точкой разрыва первого рода.

При этом если , то число h = называют скачком функции f(x) в точке x₀.

Если же , то x₀ называют точкой устранимого разрыва.

П олагая, , получим функцию непрерывную в точке x₀. В этом случае говорят, что функция f(x) доопределена по непрерывности в точке x₀.

Пример 2.23.

Рассмотрим функцию . В точке х₀ = 1 она не определена, следовательно, х₀ = 1 - точка разрыва.

Имеем , откуда х₀ = 1 – точка устранимого разрыва.

Г

у

рафик рассматриваемой функции приведен на рис.2.7

у=f(x)

2

х

0

1

рис. 2.7

Доопределим по непрерывности исходную функцию в точке х₀ = 1,

Функция непрерывна на всей числовой оси (см. рис.2.8.).

у=

у

2

х

0

1

рис. 2.8.

Пример 2.24.

Функция f(x)=[x] имеет бесконечно много точек разрыва первого рода (см. рис. 2.5). В каждую из этих точек данная функция имеет скачок h = 1.

Определение 2.20.

Пусть точка x₀ есть точка разрыва функции f(x). Если хотя бы один из односторонних пределов , бесконечен или не существует, то x₀ называется точкой разрыва второго рода.

Пример 2.25.

Рассмотрим функцию f(x)= . Точка x₀ = 0, в которой функция не определена, является точкой разрыва.

Вычислим односторонние пределы

Таким образом, точка x₀ = 0 – точка разрыва второго рода.

Схематичный график функции представлен на рис. 2.9.

у

1

х

0

рис. 2.9.