Глава VI. Неопределенный интеграл
6.1. Первообразная и неопределённый интеграл
Определение 6.1.
П
усть
функции и заданы на некотором
множестве Х. Функция F(x)
называется первообразной функции f(x),
если для всех
.
Теорема 6.1.
Е
сли
Ф(х) и F(x)–
две первообразные для одной и той же
функции f(x)
на некотором множестве
,
то , где С – произвольная
постоянная.
Определение 6.2.
Совокупность всех первообразных функции f(x), выражаемая формулой F(x)+C, называется неопределённым интегралом от этой функции, называется подынтегральной функцией, f(x)dx- подынтегральным выражением, а х – переменной интегрирования.
Обозначение:
.
6.2. Основные свойства неопределенного интеграла
Свойство 1.
Производная от
неопределенного интеграла равна
подынтегральной функции, то есть
.
Свойство 2.
Дифференциал от
неопределенного интеграла равен
подынтегральному выражению, то есть
.
Свойство 3.
Неопределённый
интеграл от дифференциала некоторой
функции равен этой функции, с точностью
до постоянного слагаемого, то есть
.
Свойство 4.
Постоянный множитель
выносится за знак интеграла, то есть
.
Свойство 5.
Неопределённый
интеграл от алгебраической суммы двух
функций равен алгебраической сумме
интегралов от этих функций, то есть
.
6.3.Таблица основных неопределённых интегралов
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
6.4. Основные методы интегрирования
1) Метод непосредственного интегрирования
При данном методе неопределенный интеграл можно отыскать с помощью свойств неопределенного интеграла, таблицы интегралов и тождественных преобразований.
Пример 6.1.
Н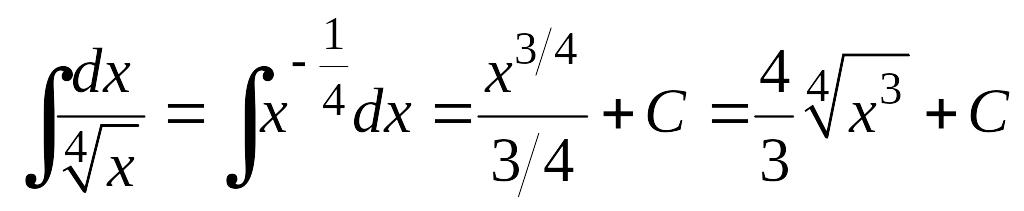
епосредственным
интегрированием найдем интеграл
(используется формула 1 таблицы 6.3, где = -1/4).
Пример 6.2.
Н
епосредственным
интегрированием найдем интеграл
(используется формула 3 таблицы 6.3, где а = 2е).
Пример 6.3.
Н
епосредственным
интегрированием найдем интеграл
(используются формула 15 из таблицы 6.3, где а2 = 8 и свойства 3, 5 из 6.2).
2) Метод подведения под знак дифференциала
Напомним, что
,
если
.
При интегрировании бывает удобно
представить
или
,
или
,…
и т.д.
Это и используется при интегрировании методом подведения под знак дифференциала.
Пример 6.4.
Методом подведения под знак дифференциала найдем интеграл
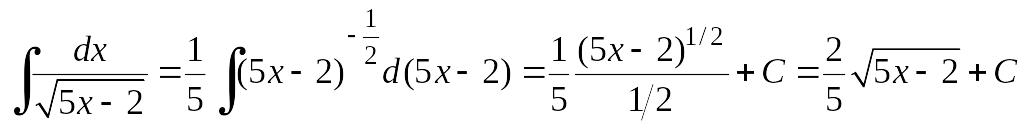
(здесь
).
Пример 6.5.
Методом подведения под знак дифференциала найдем интеграл
,
(здесь u(x) = cosx, du= (cosx)dx = -sinxdx).
Пример 6.6.
М
етодом
подведения под знак дифференциала
найдем интеграл
(здесь
).