2 .3. Предел функции при . Бесконечно малые и бесконечно большие функции.
Определение 2.8.
Пусть функция f(x)
определена на некотором множестве
,
то есть определенa
при достаточно больших по модулю
значениях x.
Число а
называется пределом
функции f(x)
при
,
если для любого положительного числа
существует положительное число
такое, что
,
если
.
Обозначение:
.
Замечание 2.2.
Если x
стремится к бесконечности, принимая
лишь положительные (отрицательные)
значения, то соответствующий предел
обозначается символом
.
Замечание 2.3.
С геометрической
точки зрения
равенство
означает, что график функции f(x)
неограниченно приближается к горизонтальной
прямой y=a.
Пример 2.6.
Доказать, что
.
Решение
Рассмотрим произвольное положительное число . Неравенство
равносильно
неравенству
.
П
оложим
, тогда если
,
то
,
а значит,
.
Таким образом,
.
Схематичный график
функции
представлен на рисунке 2.2.
О
х
у
рис. 2.2.
1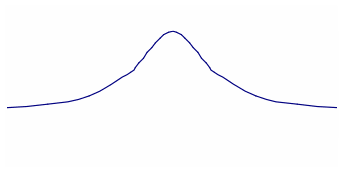
Определение 2.9.
Функция f(x)
называется бесконечно
малой функцией
при
,
если
.
Определение 2.10.
Функция f(x)
называется бесконечно
большой функцией
при
,
если функция
есть бесконечно малая функция при
.
Обозначение: .
Замечание 2.4.
В том случае, когда
f(x) принимает
только положительные (отрицательные)
значения при всех
х, близких
к точке
,
(
).
Пример 2.7.
Функция
является бесконечно малой функцией при
х
0
(
=0),
а функция
- бесконечно большой функцией при х →
1(
).
Теорема 2.2. (о свойствах бесконечно малых и бесконечно больших функций).
1. Произведение бесконечно малой (большой) при функции на постоянную, отличную от нуля, есть бесконечно малая (большая) при функция.
2. Произведение двух бесконечно малых (больших) при функций есть функция бесконечно малая (большая) при .
3. Сумма двух бесконечно малых при функций есть бесконечно малая при функция.
Замечание 2.5.
Свойство 3 для бесконечно больших функций вообще говоря не выполняется.
2.4. Основные теоремы о функциях, имеющих конечные пределы
Теорема 2.3. (о единственности предела функции)
Пусть функция f(x) имеет конечный предел в точке , тогда такой предел единственный.
Теорема 2.4. (о связи функции, имеющей конечный предел, с бесконечно малой функцией).
Для того, чтобы
функция f(x)
имела конечный
предел а
в точке
необходимо и достаточно, чтобы она была
представлена в виде
,
где
- бесконечно малая функция при
.
Теорема 2.5. (об арифметических свойствах пределов).
Пусть функции f(x) и g(x) имеют в точке конечные пределы, тогда:
1)
/R;
2)
;
3)
;
4)
.
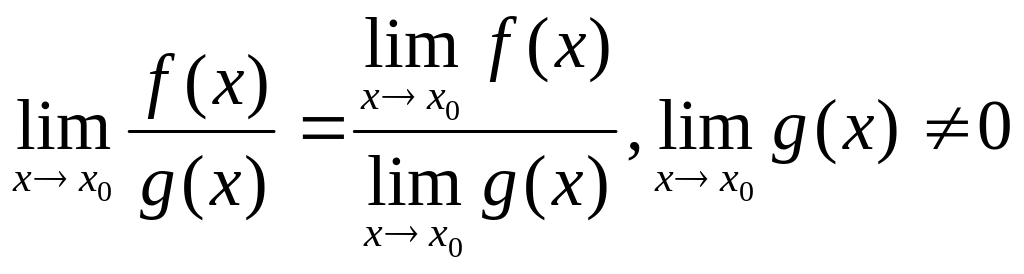Пример 2.8.
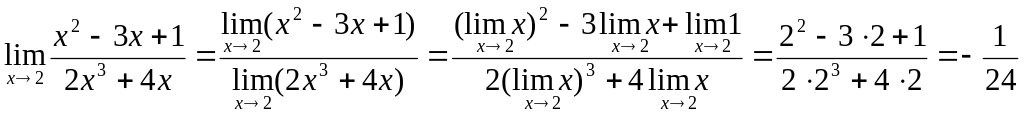
Теорема 2.6. (о замене переменной при вычислении предела).
Если
,
то
при условии, что предел в правой части
последнего равенства существует.
2.5. Замечательные пределы
Теорема 2.7. (о первом замечательном пределе).
(х
выражено в
радианах).
Следствия
1.
2.
3.
Пример 2.9.
,
где у =
6х
(здесь используется теорема 2.5 о замене
переменной при вычислении предела).
Пример 2.10.
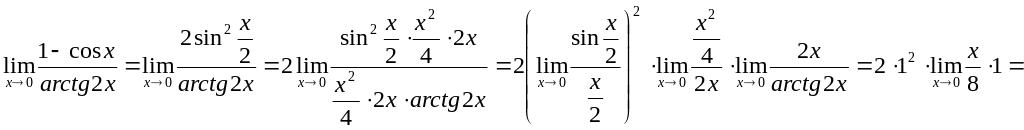
Замечание 2.6. (о числе е).
Рассмотрим
последовательность
.
Можно показать, что такая последовательность
имеет конечный предел, который обозначается
е,
то есть
е
является иррациональным числом,
вычисленным приближенно:
.
Показательная
функция
называется экспоненциональной
функцией
или экспонентой.
Логарифм положительного числа х, вычисленный по основанию е, называется натуральным логарифмом и обозначается ln x.
Экспонента и натуральный логарифм играют важную роль в математическом анализе и его приложениях.
Теорема 2.8. (о втором замечательном пределе).
Следствия
1.
2.
3.
4.
/R.
Пример 2.11.
.
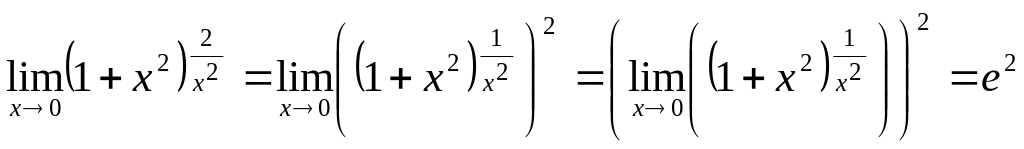Пример 2.12.
.
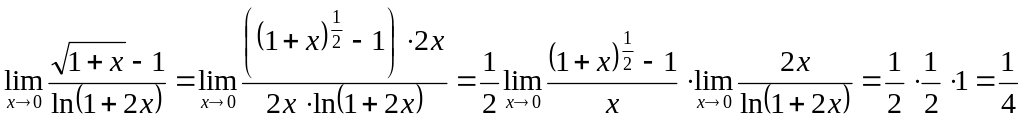