3.5. Таблица производных основных элементарных функций

1. (с)' = 0, с – константа.

2. (х^p)' = px^p-1 при всех х и p, при которых имеют смысл как х^p, так и x^p-1.

Частные случаи: (х)' = 1; (х²)' = 2х;  =

3. (а^х)' = а^х lna при а > 0, a≠1.

Частный случай: (е^х)' = е^х.

4. (log_ax)' = при a > 0, a ≠ 1, 0 < x < +∞.

Частный случай: (lnx)′ = , 0 < x < +∞

5. (sin x)' = cos x.

6. (cos x)' = - sin x.

7. (tg x)' = .

8. (ctg x)' = .

9. (arcsin x)' = при -1 < 0 < 1.

10. (arccos x)' = - при -1 < 0 < 1.

11. (arctg x)' = .

12. (arcctg x)' = - .

В формулах, рядом с которыми не приведены ограничения на значение аргумента х, предполагается, что х – любое вещественное число.

Пример 3.5.

Найдем производную функции у = sin x · arctg x + . При нахождении производной будем использовать теорему 3.3 и таблицу производных.

у' = (sin x)' arctg x + sin x (arctg x)' +

.

Пример 3.6.

Найдем производную сложной функции у = tg³x.

Данная функция состоит из внешней функции f(u) = u³ и промежуточного аргумента u = g(x) = tg(x). Так как f'(u) = 3u², u' = g'(x) = , то согласно теореме 3.5 имеем у' = 3tg²x· = .

Пример 3.7.

Найдем производную сложной функции у = (arcsin x)^x.

На первом этапе решения задачи прологарифмируем обе части данного равенства: ln y = x ·ln arcsin x.

Далее, используя правила дифференцирования сложной функции и произведения функций, получим

откуда у' = у или

у' = (arcsin x)^x .

Такой способ нахождения производной называется логарифмическим дифференцированием.

3.6. Дифференциал функции

Теорема 3.6. (о необходимом и достаточном условии дифференцируемости функции).

Рассмотрим в точке х₀ приращение функции f(x), то есть Δy=f(x₀ + Δx) – f(x₀).

Для того, чтобы функция f(x) была дифференцируема в точке х₀, необходимо и достаточно, чтобы выполнялось следующее равенство Δy=АΔх + о(Δх), Δх→0. При этом А = f'(x₀).

Определение 3.6.

Дифференциалом функции f(x) в точке х₀ называется линейная функция f′(x₀)Δx относительно аргумента Δx.

Обозначение: df(x₀) = f′(x₀)Δx.

(Другое обозначение: dy).

Найдем дифференциал функции y = x в произвольной точке х:

dx = (x)′ Δx = Δx.

Таким образом, имеем df(x₀) = f′(x₀)dx или dy = f′(x₀)dx.

Используя понятие дифференциала, можно по-другому записать равенство из теоремы 3.6: Δy=dΔх + О(Δх), Δх→0 или в развернутом виде f(x₀ + Δx) – f(x₀)= f'(х₀) Δх + О(Δх), Δх→0.

Замечание 3.2. (о приближенном вычислении значения функции).

Отбросив в последнем равенстве слагаемое О(Δх), то есть заменяя приращение функции ее дифференциалом, получим приближенное равенство f(x₀+ Δx) ≈ f(x₀) + f'(x₀)Δх. Его используют для вычисления приближенного значения f(x₀ + Δx) при малых Δх, если известны значения f(x₀) и f'(x₀).

Пример 3.8.

Вычислим приближенно е ^-0,08. Возьмем число х₀ = 0, близкое к х = -0,08 и такое, что значение функции легко вычисляется, при этом Δх = -0,08. Кроме того, заметим, что ( )' = е^х, следовательно, = = e⁰. Имеем , откуда

3.7. Дифференцирование параметрически заданной функции

Определение 3.7.

Задание функции у = у(х) с помощью двух уравнений называется параметрическим заданием функции.

Теорема 3.7. (о дифференцировании функции, заданной параметрически).

Пусть функции х = φ(x), y = ψ(t) дифференцируемы в точке t₀ T и φ'(t₀) ≠ 0, тогда функция у = у(х), заданная параметрическими уравнениями, дифференцируема в точке х₀ = φ(t) и имеет место равенство, у'(х₀) = .

Пример 3.9.

Вычислим в точке х₀ = производную функции у = у(х), параметрически заданной уравнениями: .

Из первого уравнения получим t₀ = arccos .

φ'(t) = (2 cos t)'= -2 sin t, откуда φ'(t₀) = -2 sin . ψ'(t) = (3 sin t)'= 3 cos t, откуда ψ'(t₀) = 3cos . Таким образом, у'(х₀) = .
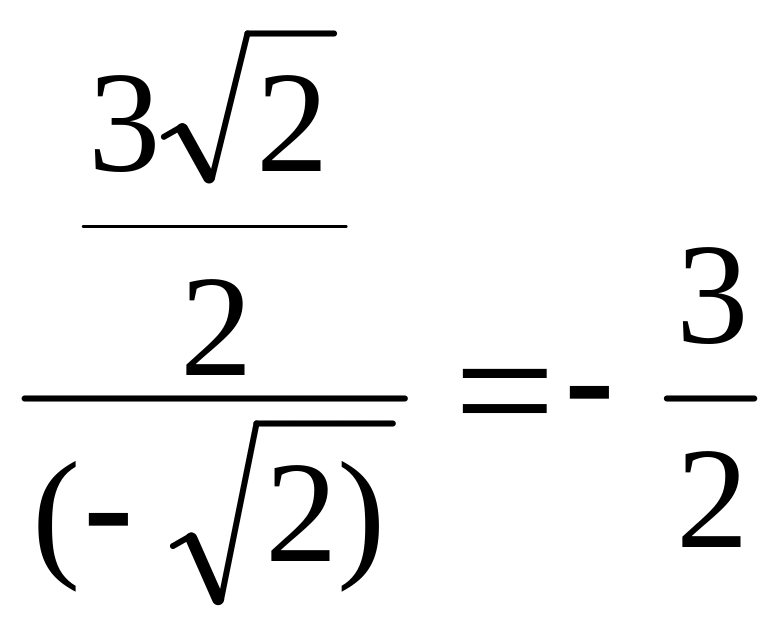