3) Метод замены переменной

Теорема 6.2.

Е сли невозможно найти предыдущими способами, но при замене переменной x=(t), где функция (t) непрерывна вместе со своей производной (t) и имеет обратную функцию ^--1(t), интеграл вычисляется, то

П ример 6.7.

Найдем интеграл методом замены переменной.

Сделаем подстановку: откуда x = t² – 1, dx = 2tdt.

.

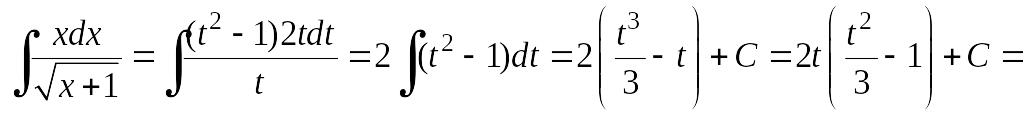
П ример 6.8.

Найдем интеграл методом замены переменной.

Заменим или e^x = t² + 1, откуда x = ln(t² + 1), dx = .

.

4) Метод интегрирования по частям

Теорема 6.3.

Е сли и – непрерывны вместе со своими производными на некотором промежутке Х, то имеет место формула , или

Замечание 6.1.

К u(x) следует относить множители, которые упрощаются при дифференцировании, а к v'(x) относятся множители, которые не сильно усложняются при интегрировании. Формула интегрирования по частям может применяться неоднократно.

Большая часть интегралов, берущихся по частям, может быть разбита на следующие 3 группы:

1) Интегралы вида ; ; .

Здесь за берется , а за - , , соответственно.

Пример 6.9.

Найдем интеграл методом интегрирования по частям

–

.

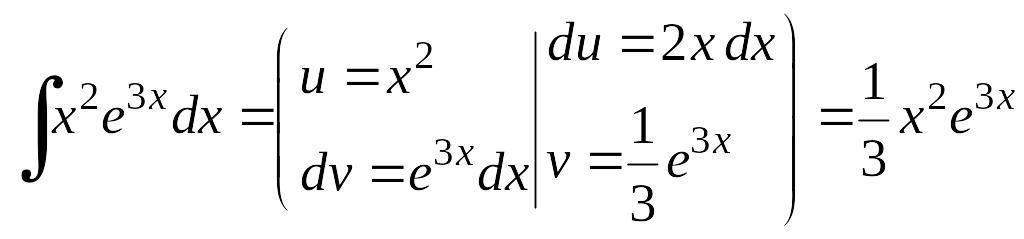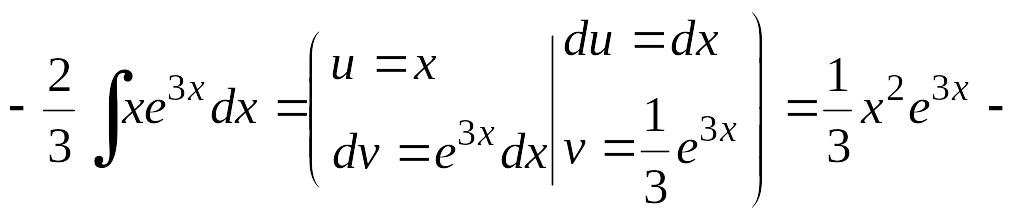
2) Интегралы вида , , .

В этом случае за u(x) нужно взять трансцендентную функцию , , , а за - .

Пример 6.10.

Найдем интеграл методом интегрирования по частям

.

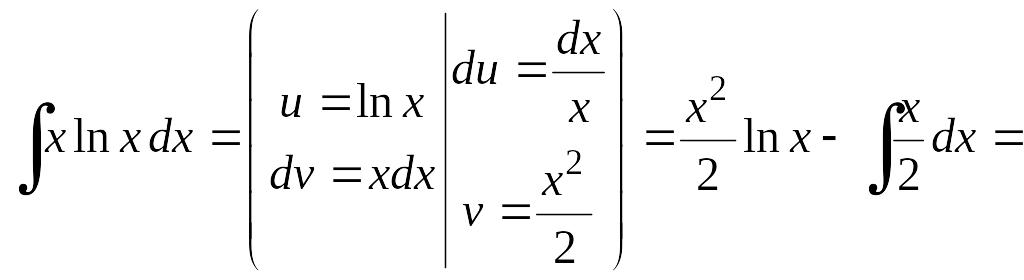
3) Интегралы вида , .

Эти интегралы берутся по частям дважды. В процессе решения приходим к уравнению относительно искомого интеграла.

Пример 6.11.

Найдем интеграл методом интегрирования по частям

= .

П олучили уравнение относительно . Решив его, получим

.

6.5. Интегрирование простейших функций, содержащих квадратный трехчлен

1) Интегралы вида ,

Они сводятся к табличным 13-16 (см. разд. 6.3) после выделения из квадратного трехчлена полного квадрата.

Пример 6.12.

Найдем интеграл

=

=

= .

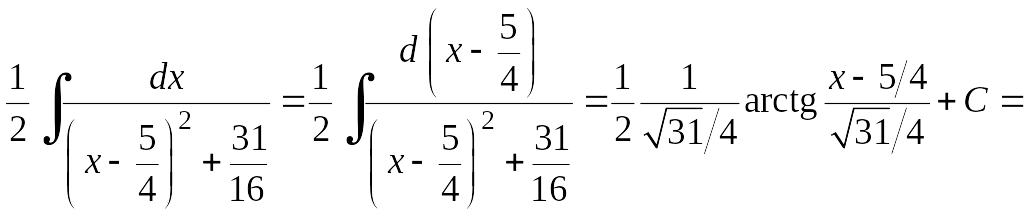
2) Интегралы вида , , (а0, m0).

При интегрировании таких функций сначала в числителе образуется дифференциал квадратного трехчлена: . Числитель преобразуется следующим образом:

.

После этого интеграл разбивается на два интеграла, первый из которых берётся по формуле 2 таблицы раздела 6.3 (u=ах2+bх+с, du=(2aх+b)dх), а второй является интегралом, рассмотренным выше.

Пример 6.13.

Найдем интеграл

.

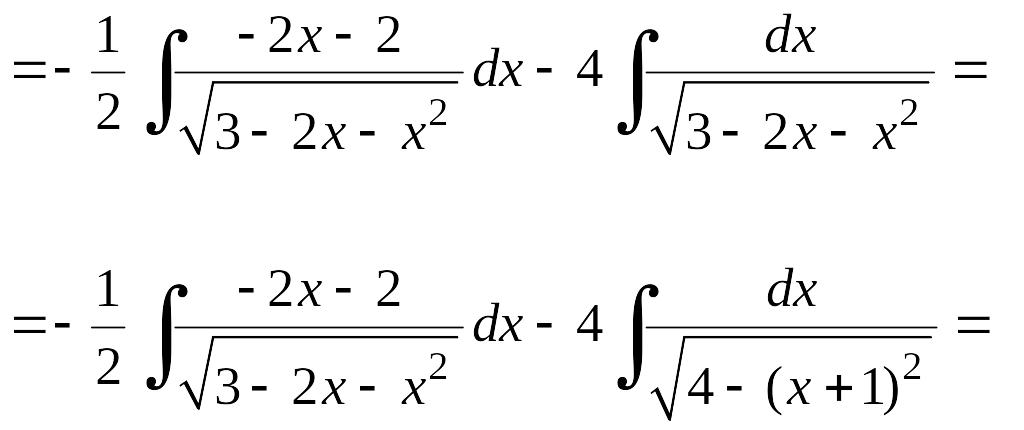
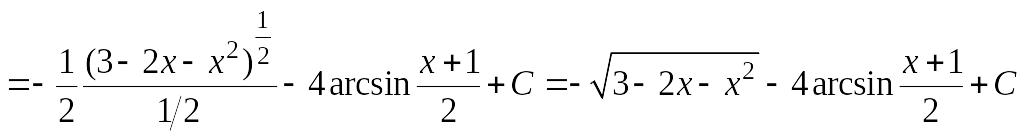
3 ) Интегралы вида .

Эти интегралы приводятся к интегралам 2) подстановкой .

Пример 6.14.

Найдем интеграл

.

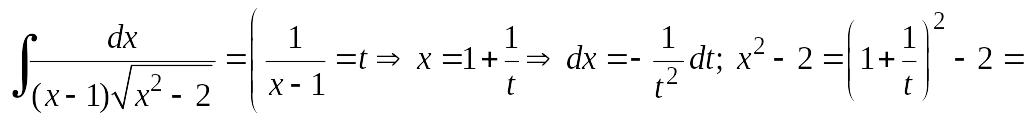
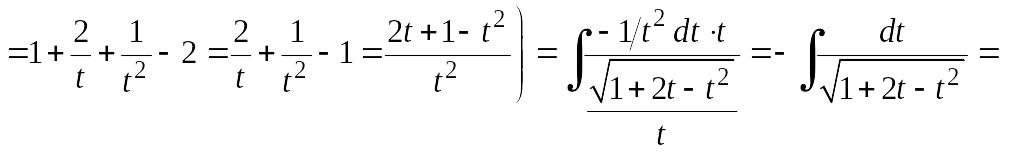
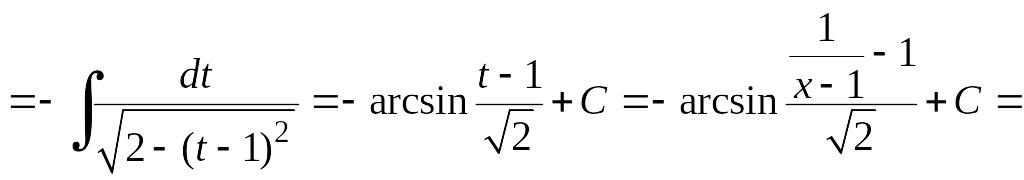
6.6. Интегрирование рациональных дробей

Определение 6.3.

Ф ункция называется дробно-рациональной или рациональной дробью, если она представляет собой дробь, в числителе и знаменателе которой стоят многочлены степени m и n соответственно. Для такой функции используют обозначение : .

Если , то дробь называется правильной, если – неправильной.

Е сли дробь неправильная, то в этой дроби можно выделить целую часть, то есть представить её в виде ,

где и – многочлены, причем , а значит, дробь – правильная. Выделение целой части производится делением числителя на знаменатель “уголком”.

П ример 6.15.

Выделим целую часть дроби .

Разделим “уголком” числитель на знаменатель:

х² + х + 1

х + 1

Ц елая часть ; S₁(x) = – 2x + 3.

Таким образом, .

О пределение 6.4.

Дроби вида , p - 4q < 0, k ≥ 2,

называются простейшими или элементарными дробями.

П равильную рациональную дробь можно разложить на сумму простейших дробей указанных четырёх типов. Это разложение зависит от разложения на множители .

П усть , где (x-a)^k соответствует вещественному корню а кратности k, а – паре комплексных сопряженных корней кратности l ( ).

В разложении на элементарные дроби сомножителю (x-a)^k будет соответствовать сумма k дробей вида

,

а сомножителю – сумма l дробей

.

О нахождении коэффициентов будет изложено ниже.

Пример 6.16.

Не определяя коэффициентов, запишем разложение правильной дробно-рациональной функции

на элементарные дроби.

В разложении знаменателя дроби R(x) на множители соответствует вещественному корню x = 0 кратности 3, x - 4 – вещественному простому корню , – паре простых комплексных сопряженных корней ; – паре комплексных сопряженных корней кратности 2. Тогда разложение на элементарные дроби будет выглядеть так:

.

Рассмотрим интегрирование каждой из простейших дробей.

1) Дробь I типа .

2) Дробь II типа .

3) Дробь III типа , .

Создадим в числителе дифференциал знаменателя, т.е. выражение .

= = =

 

=

 

= =

= .

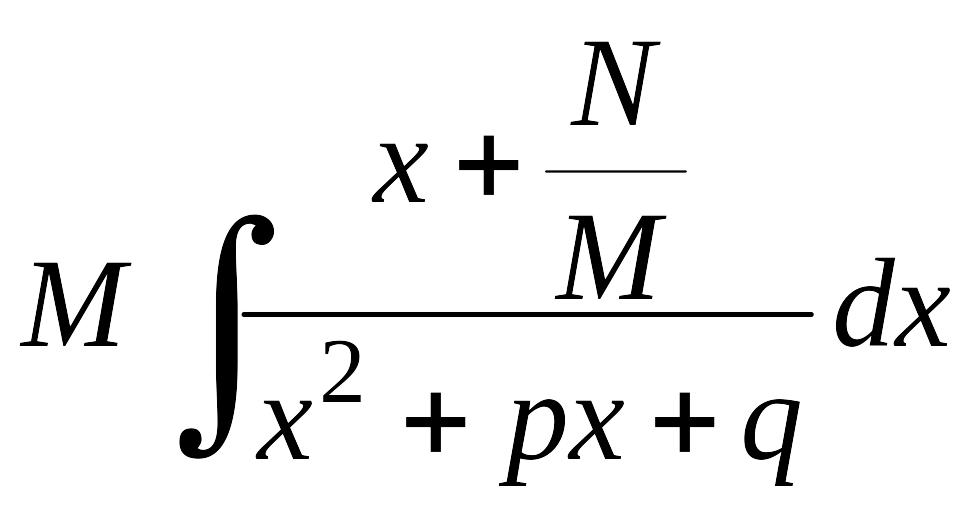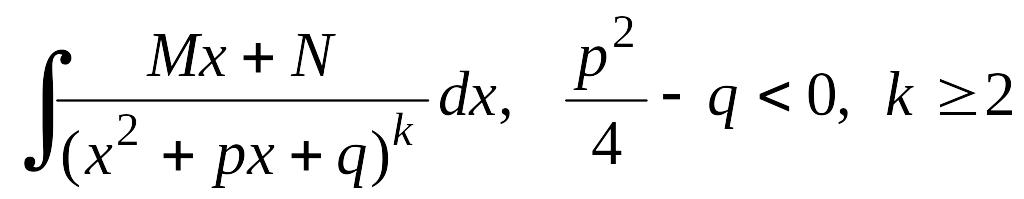
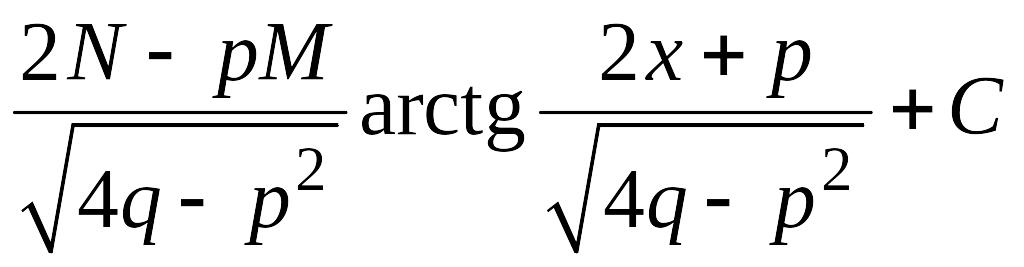4) Дробь IV типа .

И нтегрирование этих дробей после выделения в числителе дифференциала квадратного трехчлена и выделения полного квадрата в этом трехчлене сводится в вычислению двух интегралов

а ) ;

б) . (Здесь предварительно сделана замена переменной и .

Этот интеграл вычисляется по рекуррентной формуле:

.

П усть – правильная рациональная дробь. Чтобы её проинтегрировать, нужно разложить на сумму элементарных дробей, результат интегрирования которых выражается элементарными функциями.

Е сли – неправильная рациональная дробь, то можно представить в виде суммы многочлена и правильной рациональной дроби, об интегрировании которых говорилось выше.

Пример 6.18.

Н айдем интеграл .

П од интегралом стоит правильная рациональная дробь. Знаменатель её имеет вещественные простые корни . Разложим подынтегральную дробь на элементарные дроби: .

 

Приведя к целому виду обе части этого тождества, получим

. Полагая последовательно , получим систему уравнений:

Таким образом,

=

П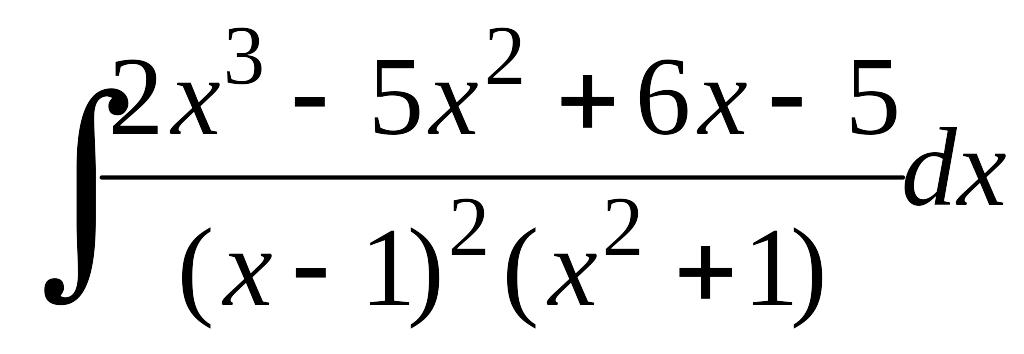 ример 6.19.

Найдем интеграл .

Под интегралом – правильная рациональная дробь. Разложение на элементарные дроби имеет вид:

,

.

Коэффициенты A, B, C, D можно найти, приравнивая коэффициенты при одинаковых степенях многочленов, стоящих в равенстве слева и справа:

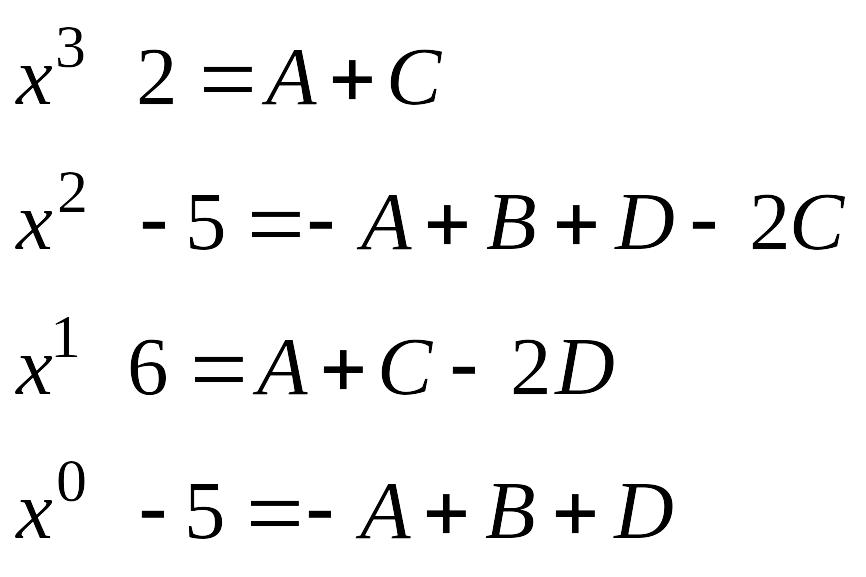
Решив систему уравнений, получим

, откуда

.

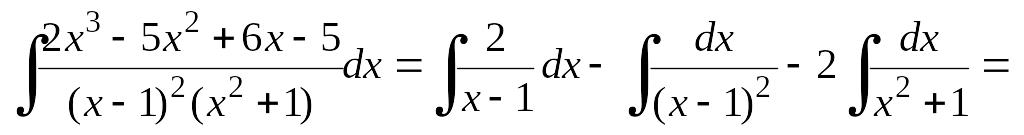
Замечание 6.2.

Часть коэффициентов можно найти, подставляя в обе части равенства значения вещественных корней знаменателя. В нашем случае это один вещественный корень х = 1. Имеем 2-5+5-5=2В, откуда В = -1.