
- •Неопределенный интеграл
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Метод замены переменных
- •Сведения из теории
- •Метод подведения под дифференциал
- •Метод подстановки
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Интегрирование по частям
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Простейшие интегралы, содержащие квадратный трехчлен
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Интегрирование рациональных дробей
- •Основные понятия
- •Интегрирование простейших рациональных дробей
- •Интегрирование правильных рациональных дробей
- •Интегрирование неправильных рациональных дробей
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Тригонометрические интегралы
- •Сведения из теории
- •Интегралы вида
- •Задачи для самостоятельного решения
- •Интегрирование некоторых иррациональных функций
- •7.1. Сведения из теории
- •7.1.1. Интегралы вида ,
- •7.1.2. Интегралы вида
- •7.1.3. Интегралы вида
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Библиографический список
Интегрирование правильных рациональных дробей
Метод интегрирования состоит в разложении правильной дроби в сумму простейших дробей и почленном интегрировании этой суммы:
а) сначала находится разложение знаменателя на линейные множители и квадратичные множители с отрицательным дискриминантом
![]() ;
;
б) по этому разложению находится вид разложения правильной дроби в сумму простейших
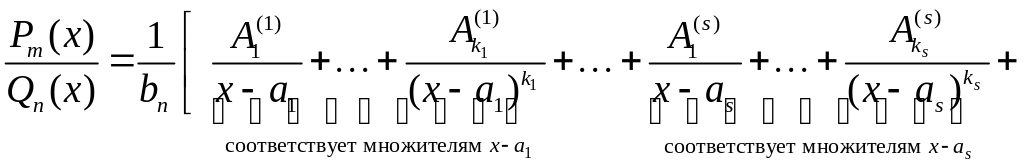 (5.5)
(5.5)
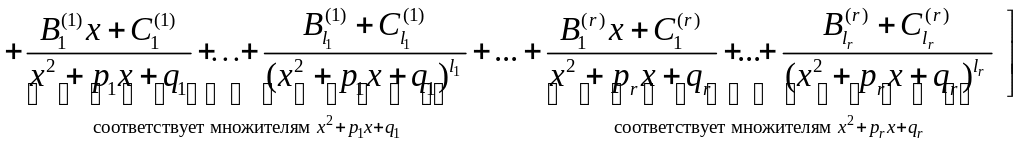 ;
;
с)
коэффициенты
![]() в этом разложении находятся из уравнений,
получающихся при приравнивании
коэффициентов при одинаковых степенях
x
у многочлена
в этом разложении находятся из уравнений,
получающихся при приравнивании
коэффициентов при одинаковых степенях
x
у многочлена
![]() и многочлена, который получается в
числителе правой части равенства (5.5)
после её к общему знаменателю (см. задачи
5.2.2 и 5.2.3).
и многочлена, который получается в
числителе правой части равенства (5.5)
после её к общему знаменателю (см. задачи
5.2.2 и 5.2.3).
Другой приём нахождения коэффициентов состоит в том, что после приравнивания числителей левой и правой частей равенства (5.5) полагают переменную x равной различным числам, в первую очередь, корням знаменателя (см. задачу 5.2.1).
Интегрирование неправильных рациональных дробей
С помощью деления “уголком” неправильную дробь можно представить в виде суммы многочлена (целой части) и правильной дроби (см. задачу 5.2.4); тем самым интегрирование неправильной дроби сводится к рассмотренной выше задаче интегрирования правильной дроби.
Примеры решения задач
5.2.1.
Вычислить
![]() .
.
◄ Рассматриваемая дробь правильная, так как степень числителя меньше степени знаменателя.
Знаменатель дроби разложим на линейные множители:
![]() .
.
Теперь ищем разложение дроби на сумму простейших в виде
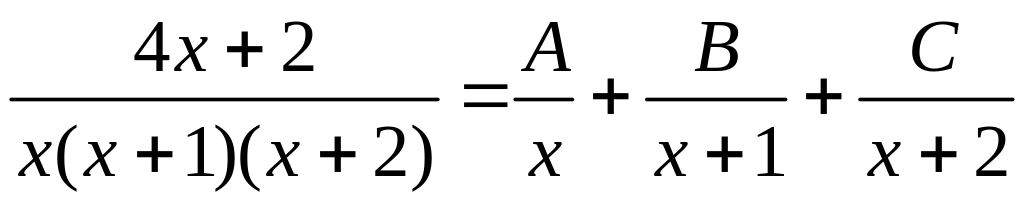 ,
,
где
A,
B
и C
подлежат определению. Множителю x
в знаменателе соответствует простейшая
дробь
![]() ,
множителю
,
множителю
![]() – дробь
– дробь![]() ,
множителю
,
множителю
![]() – дробь
– дробь
![]() .
.
Для нахождения A, B и C приведём правую часть к общему знаменателю
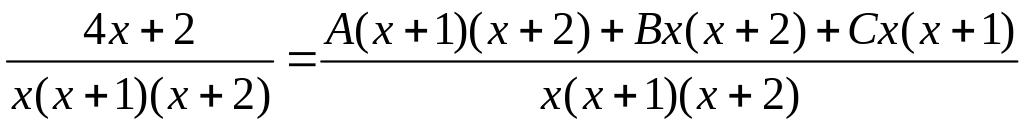 .
.
Так как знаменатели дробей, стоящих слева и справа одинаковые, то должны быть равны и числители:
![]() .
.
Полагая в этом тождестве x равным корням знаменателя, получаем уравнения для нахождения А, В и С:
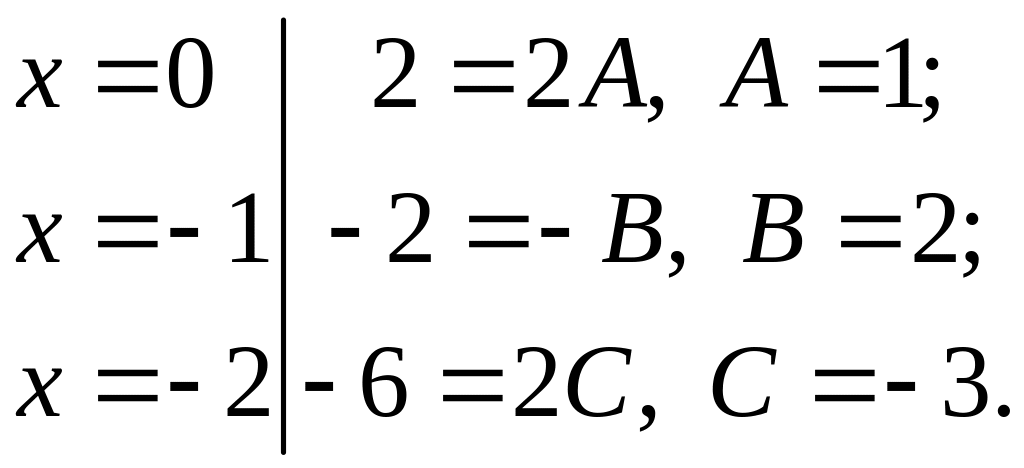
Итак,
![]() .
.
![]() .►
.►
5.2.2.
Вычислить
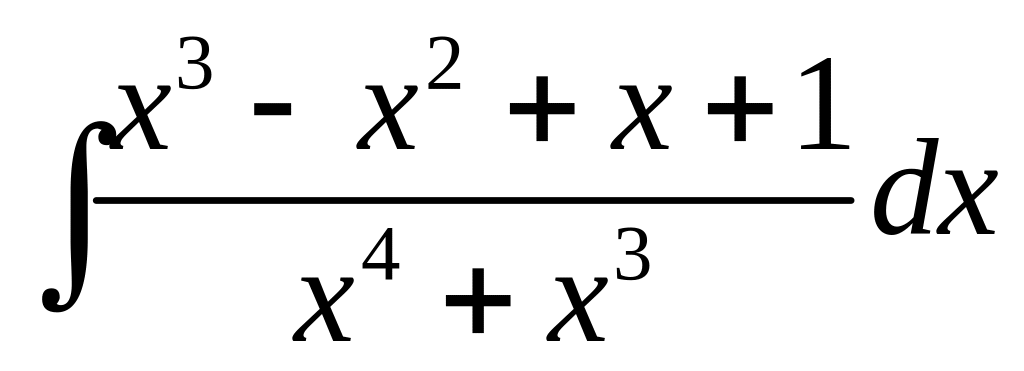 .
.
◄ Дробь, стоящая под знаком интеграла, правильная. Её знаменатель разлагается на линейные множители
![]() .
.
Поэтому разложение дроби в сумму простейших имеет вид
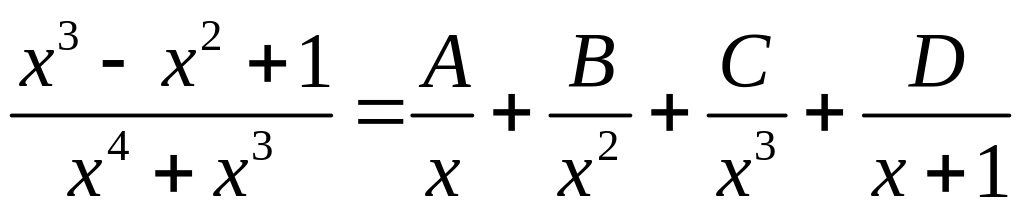 . (5.6)
. (5.6)
Здесь
первые три слагаемых соответствуют
множителям x
(их три), а четвёртое – множителю
![]() .
Приводим правую часть этого равенства
к общему знаменателю
.
Приводим правую часть этого равенства
к общему знаменателю
![]() ,
и приравниваем числители
,
и приравниваем числители
![]()
или
![]() .
.
Для нахождения неизвестных A, B, C, D используем равенство коэффициентов при одинаковых степенях x в многочленах, стоящих справа и слева от знака равенства.

Поставляя найденные значения A, B, C, D в (5.6) и интегрируя, получаем
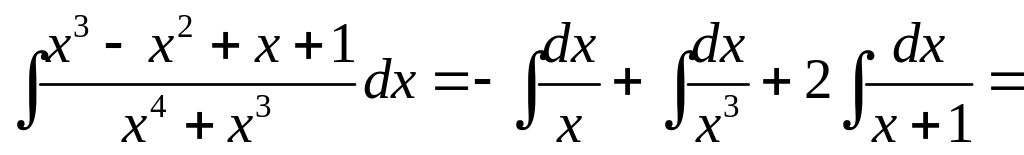
![]() .►
.►
5.2.3.
Вычислить
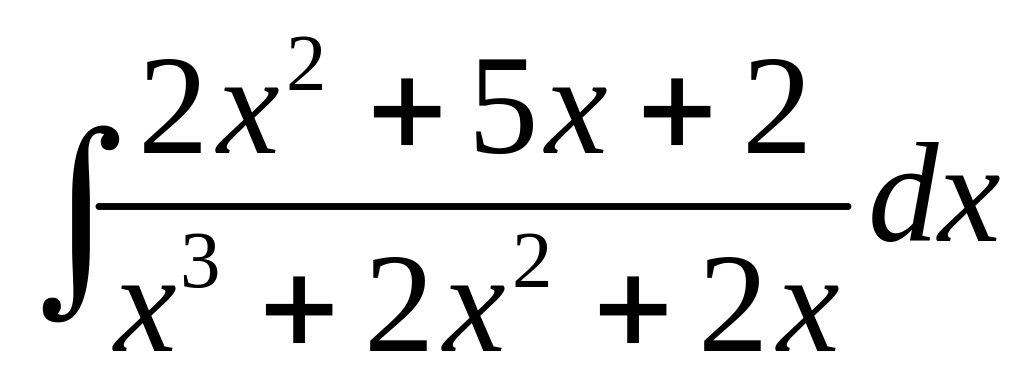 .
.
◄
Дробь
правильная. Знаменатель разлагается в
произведение линейного и квадратичного
множителей:
![]() .
.
Квадратный
трёхчлен
![]() имеет отрицательный дискриминант и на
линейные множители не разлагается.
Поэтому
имеет отрицательный дискриминант и на
линейные множители не разлагается.
Поэтому
![]() .
.
Освободимся от знаменателя и найдём A, B и С, используя те же приёмы, что и в предыдущих примерах.
![]()
![]() ,
,![]() ,
,
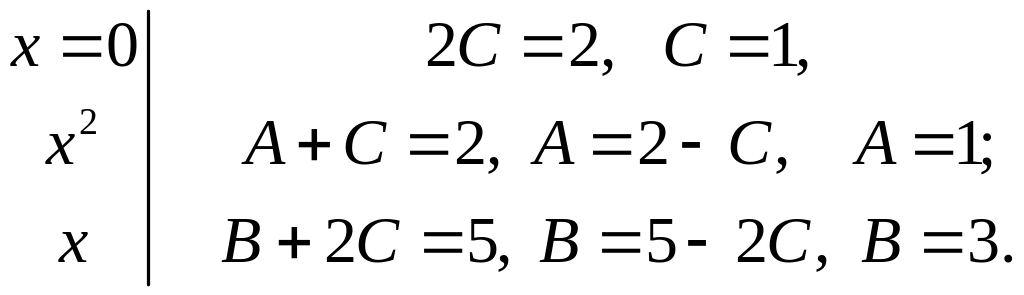
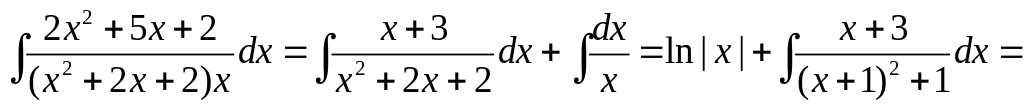
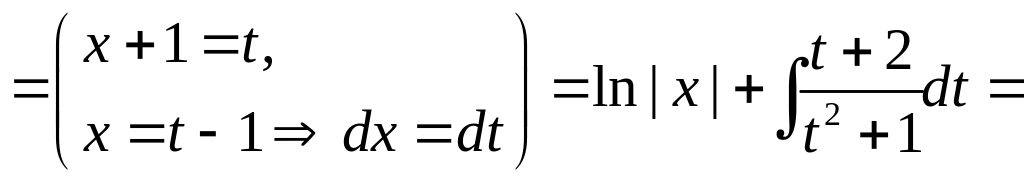
![]()
![]()
![]() .
►
.
►
5.2.4.
Вычислить
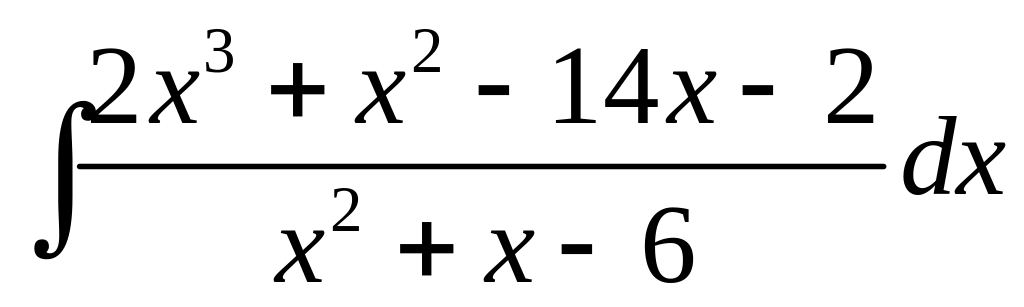 .
.
◄Дробь, стоящая под знаком интеграла, неправильная, поэтому её надо представить в виде суммы многочлена (целой части) и правильной дроби, выполнив деление многочлена (числителя дроби) на многочлен (знаменатель дроби).

Получаем
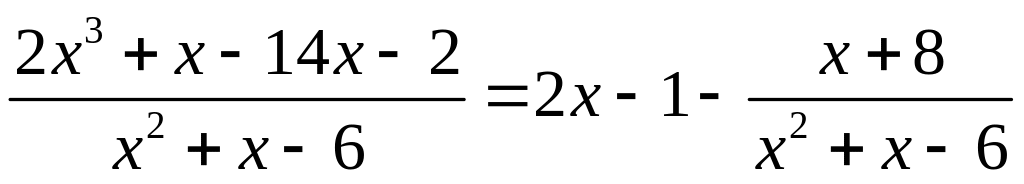 .
Дробь
.
Дробь
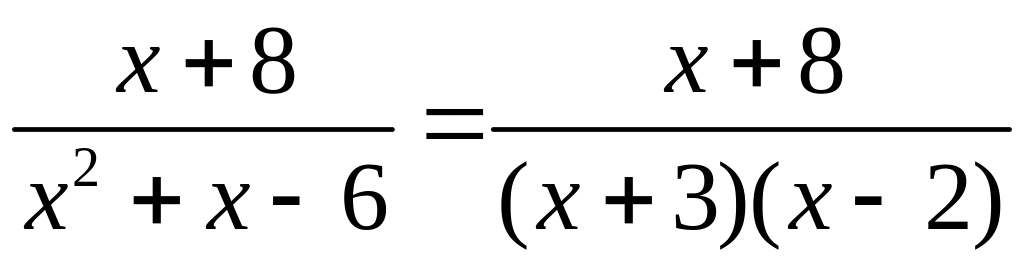 правильная. Её можно представить в виде
суммы двух простейших дробей
правильная. Её можно представить в виде
суммы двух простейших дробей
![]() (выкладки мы опустили). Поэтому
(выкладки мы опустили). Поэтому
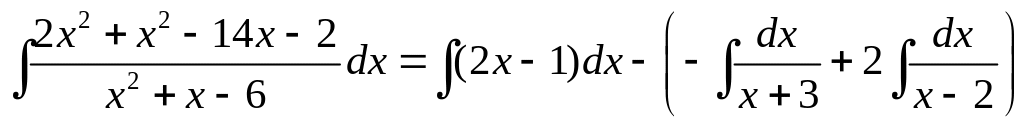 =
=
![]() .
►
.
►
