7.1.4. Задачи
Привести к каноническому виду методом Лагранжа следующие квадратичные формы:
1.
.
2.
.
3.
.
4.
.
5.
.
Привести к каноническому виду методом Якоби, если это возможно, следующие квадратичные формы:
6.
.
7.
.
8.
.
9.
.
10.
.
Найти ортогональное преобразование, приводящее следующие квадратичные формы к каноническому виду и записать этот вид.
11.
.
12.
.
13.
.
14.
.
15.
.
16.
.
Найти канонический вид, к которому следующие квадратичные формы приводятся ортогональным преобразованием
17.
.
18.
.
7.2. Знакоопределенные квадратичные формы
Определение.
Эрмитова квадратичная
форма
называется положительно (неотрицательно)
определенной, если
.
Эрмитова квадратичная форма называется отрицательно (неположительно определенной), если
.
Для положительной (отрицательной) определенности квадратичной формы необходимо и достаточно, чтобы все ее канонические коэффициенты в произвольном базисе имели одинаковые знаки.
7.2.1. Матрица Грама
Пусть
на комплексном пространстве Х заданы
положительно определенная эрмитова
квадратичная форма
и соответствующая ей билинейная форма
,
-
конечная система векторов пространства
Х.
Определение. Матрица
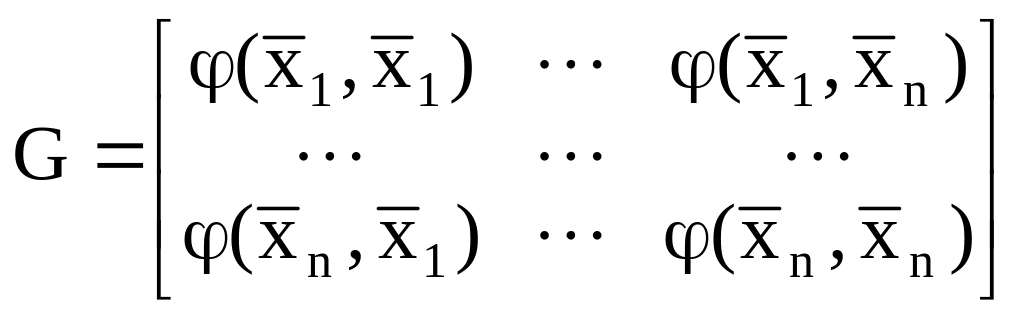
называется матрицей Грама данной системы векторов относительно формы .
Матрица Грама системы векторов относительно положительно определенной эрмитовой формы вырождена тогда и только тогда, когда эти векторы линейно зависимы.
Очевидно,
матрица
положительно определенной квадратичной
формы
является матрицей Грама базисной системы
векторов относительно
.
Пример.
Определим в
пространстве
многочленов степени
с действительными коэффициентами
билинейную форму
соотношением
,
где
.
Очевидно, соответствующая квадратичная
форма
является положительно определенной.
Построим матрицу Грама для системы
многочленов
.
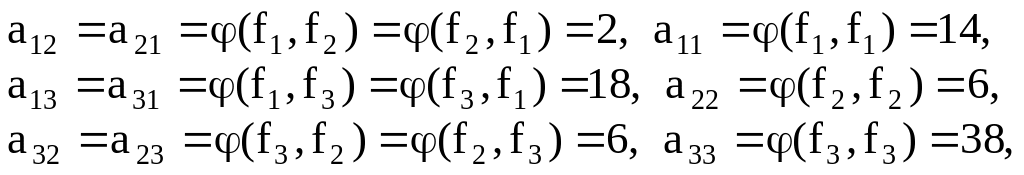
и
матрица
имеет вид
.
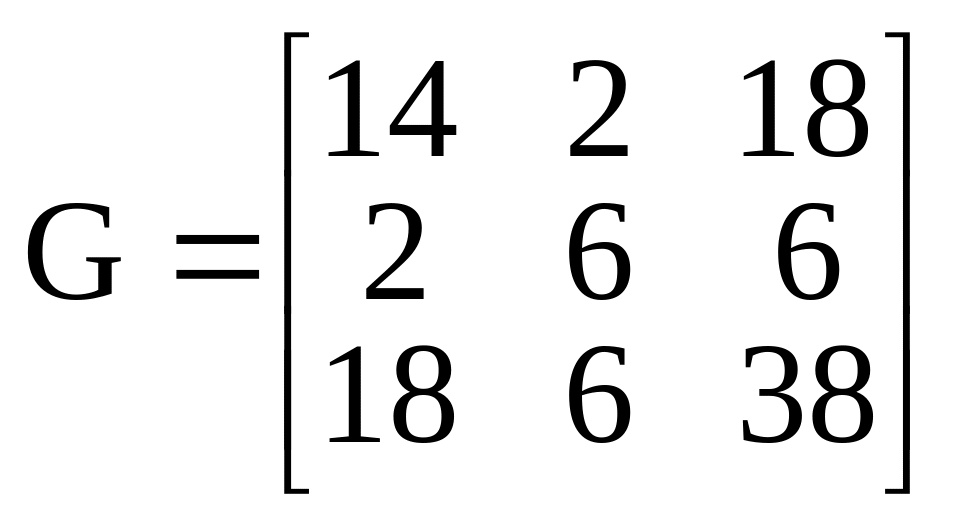Вычислив
определитель
,
убеждаемся, что многочлены
- линейно независимы.
7.2.2. Критерий Сильвестра
Для того, чтобы эрмитова квадратичная форма была положительно определена, необходимо и достаточно, чтобы все главные миноры ее матрицы были положительны, т. е.
.
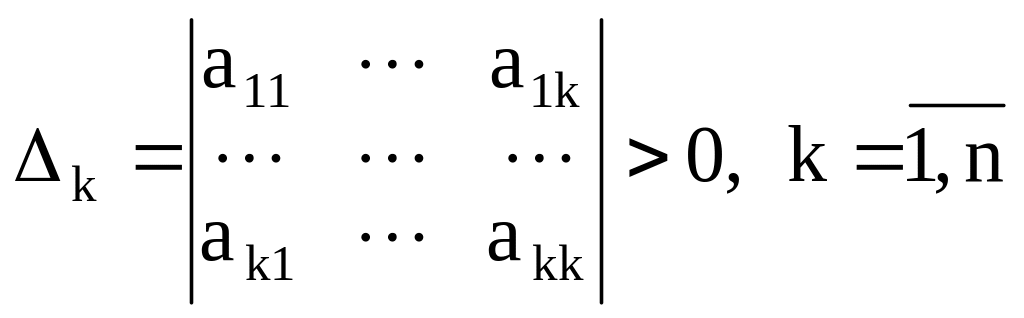Пример.
Найти все значения
параметра
,
при которых положительно определена
квадратичная форма
.
Матрица квадратичной формы
.
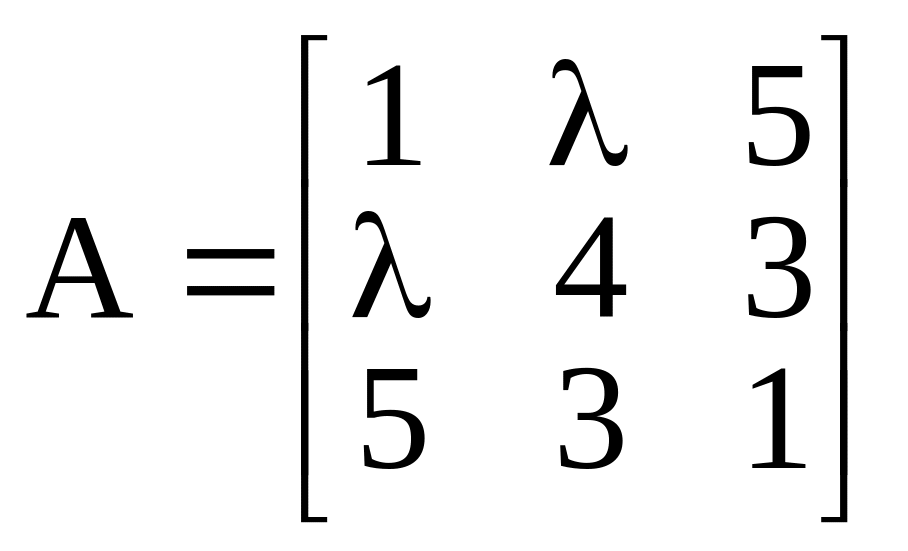Главные миноры матрицы
.
Согласно критерию Сильвестра, необходимо выполнение условий
.
Решение
первого неравенства
а решение второго
.
Одновременное выполнение этих условий
невозможно и, следовательно, квадратичная
форма не является положительно
определенной.
7.2.3. Одновременное приведение двух квадратичных форм к каноническому виду.
Пусть
и
- симметричные квадратичные формы,
заданные на вещественном пространстве,
причем одна из них, например,
-
положительно определена. Тогда существует
преобразование переменных, одновременно
приводящее эти квадратичные формы к
сумме квадратов
,
,
где
канонические коэффициенты
являются собственными значениями
матрицы
и могут быть определены как корни
алгебраического уравнения
.
Пример. Привести к каноническому виду с помощью невырожденного преобразования пару квадратичных форм
,
.
Матрицы данных форм соответственно равны
.
Используя, например, критерий Сильвестра, убеждаемся, что вторая квадратичная форма положительно определена. Поэтому задача имеет решение. Для нахождения канонических коэффициентов составляем и решаем уравнение
,
корни
которого
.
Поэтому в каноническом базисе
,
.