6.3. Полярное разложение оператора

Если А – произвольный линейный оператор, действующий в унитарном пространстве , то существует единственный неотрицательный самосопряженный оператор и унитарный оператор такие, что

.

Оператор определяется из условия , т. е. является арифметическим корнем из оператора . Оператор является единственным лишь тогда, когда оператор А невырожден. В этом случае . Для нормального оператора А операторы и перестановочны.

Пример. Построим полярное разложение оператора, который задан матрицей

.

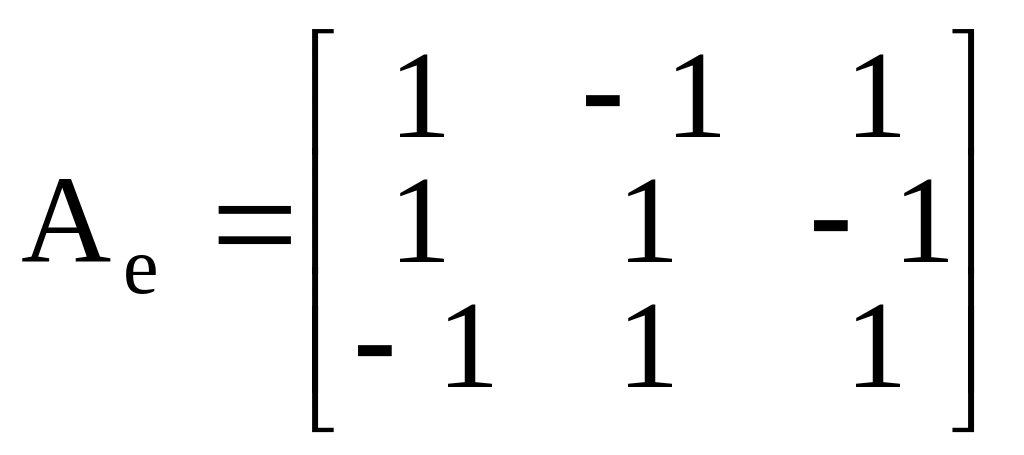Матрица сопряженного оператора имеет вид

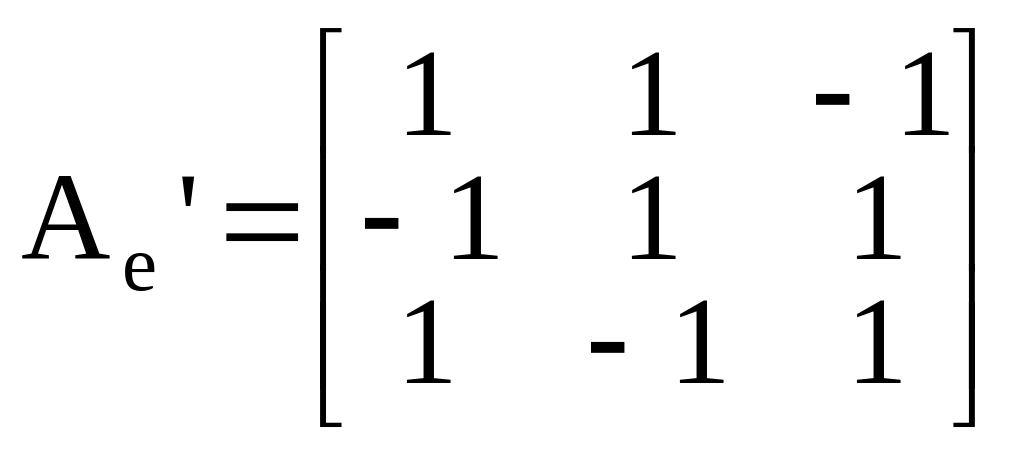
и матрица оператора тогда равна

.

Для построения матрицы необходимо найти собственные векторы и собственные значения матрицы . Решим соответствующее характеристическое уравнение

.

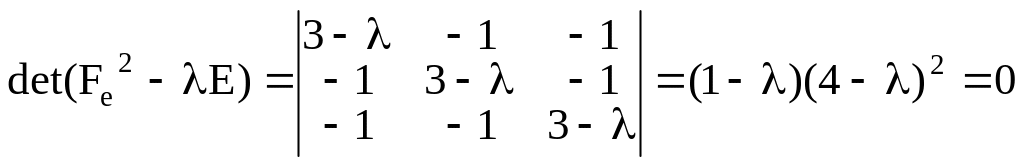Откуда собственные значения кратности и кратности .

Координаты первого собственного вектора, соответствующего , определятся системой

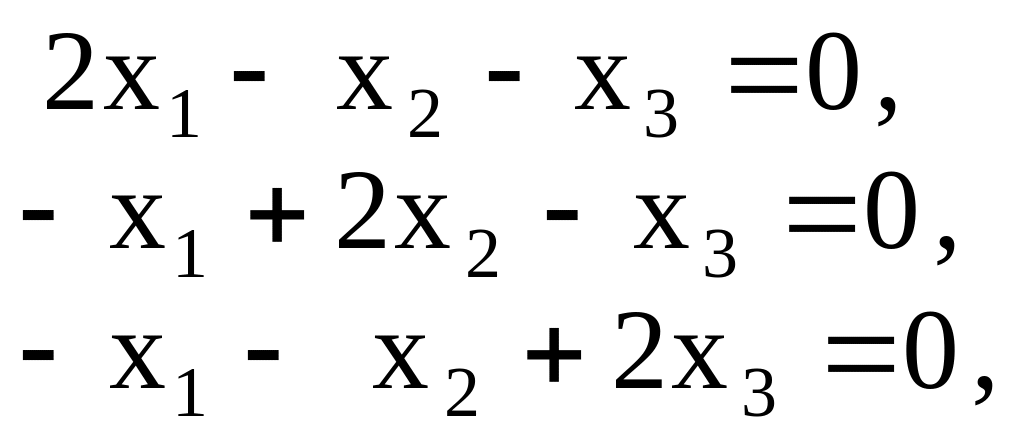
нормированное решение которой, например, вектор .

Координаты второго и третьего собственных векторов, соответствующих , определяются уравнением

,

имеющего два линейно независимых решения, например, векторы . Применяя к векторам процедуру ортогонализации Грама–Шмидта, получим еще два ортонормированных собственных вектора

.

Ортонормированная матрица перехода тогда равна

.

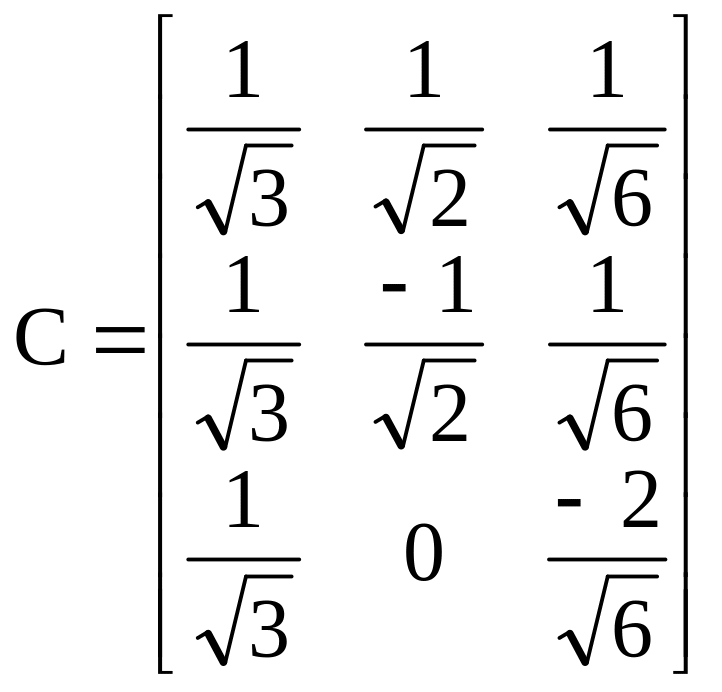Матрицы и имеют одни и те же собственные векторы и собственные значения - корни из собственных значений . Поэтому

.

Далее, , т. е. - невырожденная матрица. Поэтому матрица . Учитывая, что собственные значения обратны собственным значениям , получим

,

.

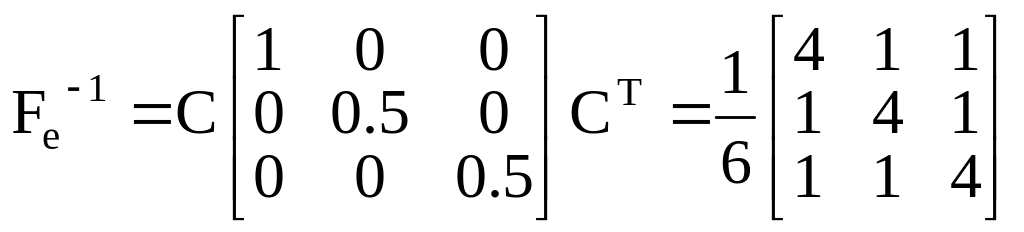Непосредственным умножением нетрудно убедиться теперь, что .

6.4. Задачи

1. Доказать, что сопряженные операторы обладают следующими свойствами:

2. Для линейных операторов, заданных следующими матрицами, найти матрицы сопряженных операторов:

.

3. Проверить, являются ли нормальными операторы, заданные в некотором трехмерном унитарном пространстве матрицами из задачи 2.

Найти ортонормированный базис из собственных векторов и матрицу в этом базисе для линейных операторов, заданных в некотором ортонормированном базисе матрицами:

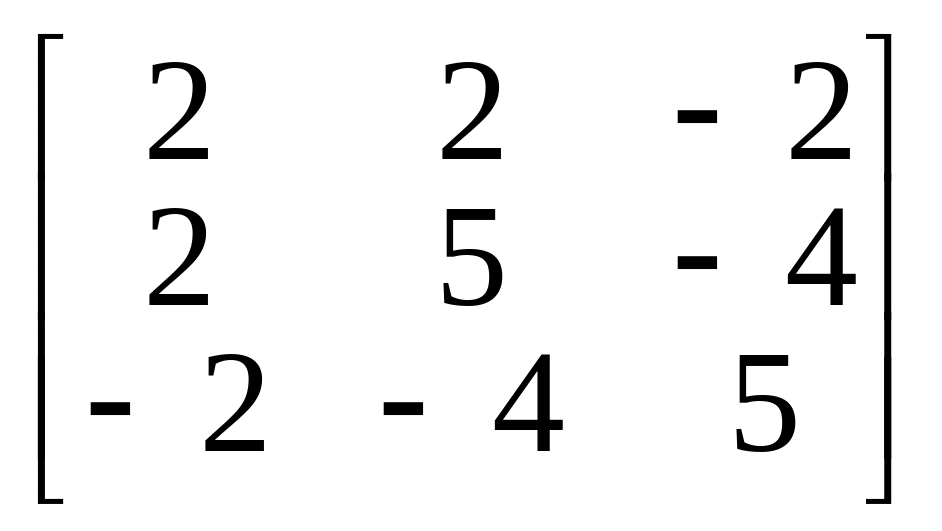4. . 5. . 6. .

7. .

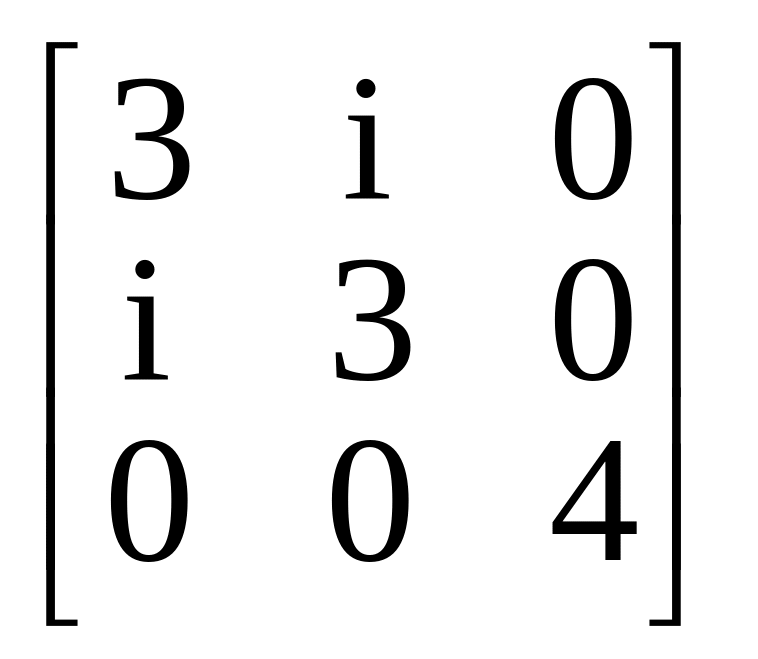Найти полярное разложение следующих матриц:

8. . 9. . 10. .

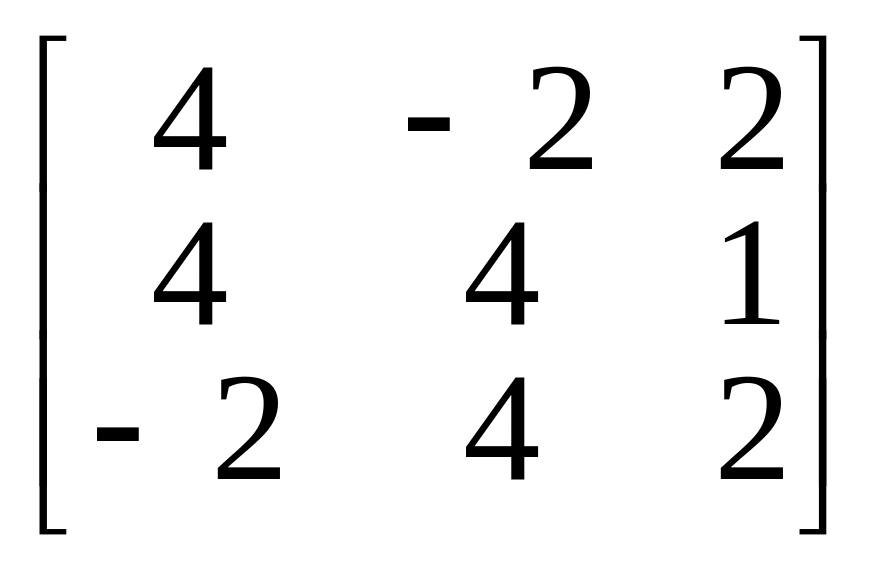Найти собственные значения матричного многочлена , если матрица равна:

11. . 12. . 13. .

2. Билинейные и квадратичные формы

Определение 1. Числовая функция двух векторных аргументов , определенная на комплексном пространстве Х, называется билинейной формой, если при каждом фиксированном она линейна по , а при каждом фиксированном сопряженно - линейна по , т. е.

Если в пространстве Х задан базис и ,то значение билинейной формы равно

,

где - значение билинейной формы на паре базисных векторов. Матрица называется матрицей билинейной формы в заданном базисе Х. В матричных обозначениях

,

где .

Если два базиса пространства и

связаны формулами перехода

,

где - матрица перехода, то матрицы А и билинейной формы в этих базисах связаны соотношением

Ранг матрицы билинейной формы называется рангом билинейной формы. При переходе от базиса к базису ранг билинейной формы не меняется.

Билинейная форма , определенная на комплексном пространстве, называется эрмитовой, если .Эрмитовой форме соответствует эрмитова матрица А, для которой .

При билинейная форма переходит в квадратичную форму . В - мерном пространстве всякая квадратичная форма имеет вид

.

Квадратичная форма с эрмитовой матрицей принимает только действительные значения.