Федеральное агентство по образованию РФ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

УТВЕРЖДАЮ

Декан ФПМК

________Горцев А.М.

Линейные операторы. Квадратичные формы

Учебно-методическое пособие

Томск

2005

РАССМОТРЕНО и УТВЕРЖДЕНО методической комиссией факультета прикладной математики и кибернетики

ПРОТОКОЛ № 22 от 18 января 2005 г.

Председатель комиссии

Профессор С.Э.Воробейчиков

В учебно-методическом пособии приведены краткие теоретические сведения и даны практические рекомендации к решению задач по курсу «Линейная алгебра и аналитическая геометрия».

Пособие разработано для студентов факультета прикладной математики и кибернетики дневной формы обучения.

Составители: К.И. Лившиц

Л.Ю. Сухотина

1. Линейные операторы. Матрица линейного оператора.

1. Определение оператора. Действия с операторами.

Определение 1. Пусть  и  - линейные пространства, заданные над одним и тем же полем . Отображение     , ставящее в соответствие каждому элементу  некоторый элемент , называется оператором, действующим из  в . При этом используются обозначения или .

Определение 2. Оператор , действующий из  в , называется линейным, если и выполняются соотношения

1. -свойство аддитивности оператора.

2. - свойство однородности оператора.

Если пространство  совпадает с , то линейный оператор  называют линейным преобразованием пространства .

Пример 1. Поставим в соответствие каждому вектору  этот же вектор .Получим линейный оператор   , который называется тождественным или единичным оператором.

Пример 2. Пусть . Пусть - ортонормированный базис в , а - его расширение до базиса в . Поставим в соответствие каждому вектору вектор , определив его следующим образом . Полученное отображение – линейный оператор, который называется оператором проектирования на подпространство.

Определение 3. Два оператора и называются равными, если .

Определение 4. Оператор называется суммой операторов и ( ), если .

Определение 5. Оператор называется произведением оператора на число , если .

Определение 6. Оператор называется произведением операторов и (С=ВА), если .

1.2. Матрица линейного оператора.

Рассмотрим линейный оператор  (линейное преобразование пространства ). Пусть векторы образуют базис пространства . Подействуем оператором А на базисные векторы. В результате получим векторы . Так как вектор , то его можно разложить по базису:

.

В результате получаем матрицу:

,

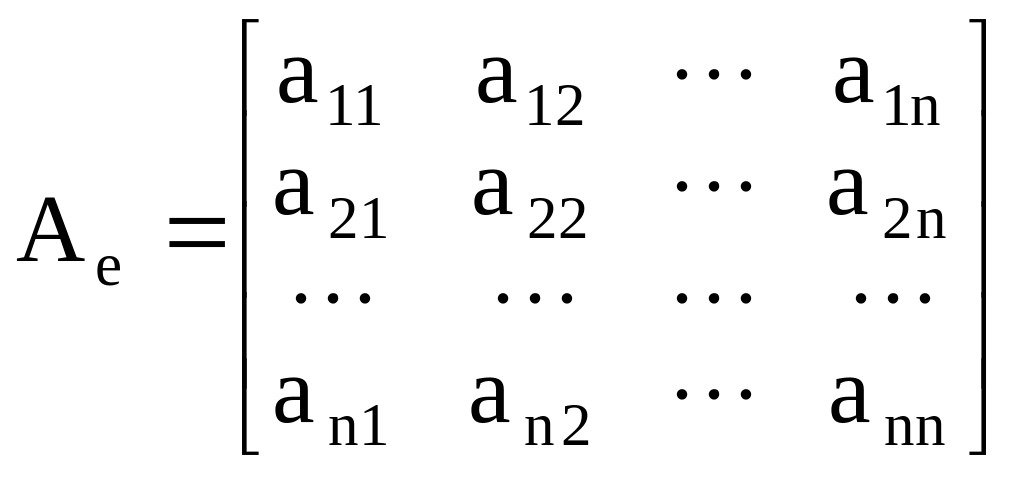i- ый столбец которой есть вектор-столбец из координат вектора в базисе . Матрица называется матрицей линейного оператора в заданном базисе .

Пусть теперь - произвольный вектор из , а - его образ при линейном преобразовании А. Тогда координаты векторов и связаны соотношением:

.

Таким образом, действие линейного оператора на вектор сводится к преобразованию его координат с помощью матрицы линейного оператора. Задание матрицы линейного оператора является наиболее удобным способом определения оператора действующего в конечномерном пространстве.

Пусть С- матрица перехода от базиса к базису ,а и - матрицы оператора в первом и втором базисе соответственно. Тогда имеют место соотношения:

.

Матрицы и , связанные между собой данными соотношениями, называются подобными матрицами.

Действиям над линейными операторами соответствуют точно такие же действия над их матрицами. Если А и В линейные операторы, действующие в Х и , - матрицы этих операторов в одном и том же базисе, то:

1. Оператору А+В соответствует матрица .

2. Оператору соответствует матрица .

3. Оператору АВ соответствует матрица .

4.Если оператор В=А^-1 , то матрица .

Пример 1. Вычислим матрицу тождественного оператора Е. По определению . Пусть базис в Х. Тогда вектор . Поэтому тождественному оператору соответствует единичная матрица:

.

Пример 2. Покажем, что поворот плоскости на угол  вокруг начала координат является линейным преобразованием, и найдем матрицу этого преобразования в любом ортонормированном базисе. Предполагается, что положительное направление отсчета углов совпадает с направлением кратчайшего поворота, переводящего базисный вектор во второй вектор базиса . Покажем, во-первых, что данный оператор является линейным. Пусть - радиус-вектор произвольной точки плоскости. Обозначим его координаты , модуль через , угол с базисным вектором через . Тогда

.

Образ вектора вектор будет равен

Рассмотрим теперь сумму двух векторов

.

Тогда образ суммы

т. е. выполняется свойство аддитивности линейного оператора. Аналогично можно проверить выполнение свойства однородности . Найдем теперь матрицу оператора в базисе , . Так как базис ортонормированный, то и . Тогда образы базисных векторов равны и . Откуда матрица оператора имеет вид

.

Пример 3. Линейный оператор А в базисе , , ,

имеет матрицу

.

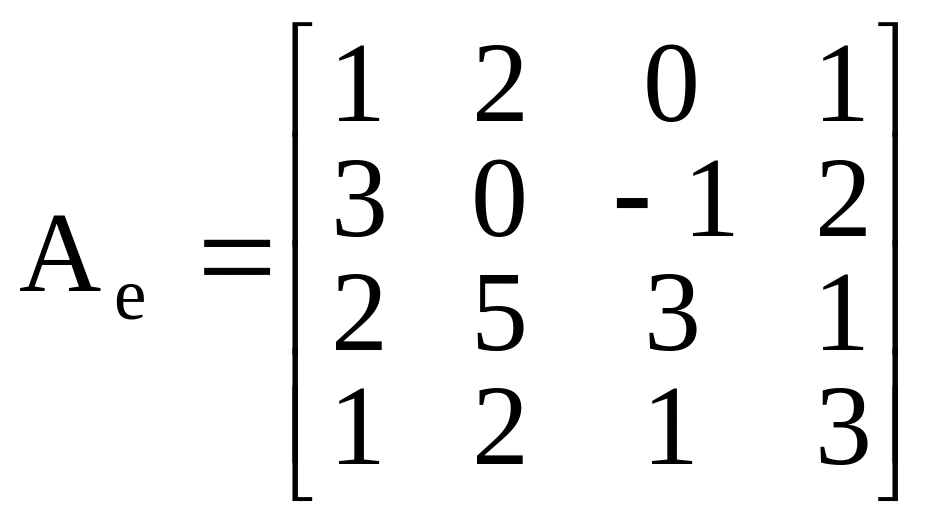Необходимо найти матрицу этого оператора в базисе , , , .

Векторы двух базисов «старого» и «нового» связаны соотношениями . Поэтому матрица перехода С от базиса к базису имеет вид:

.

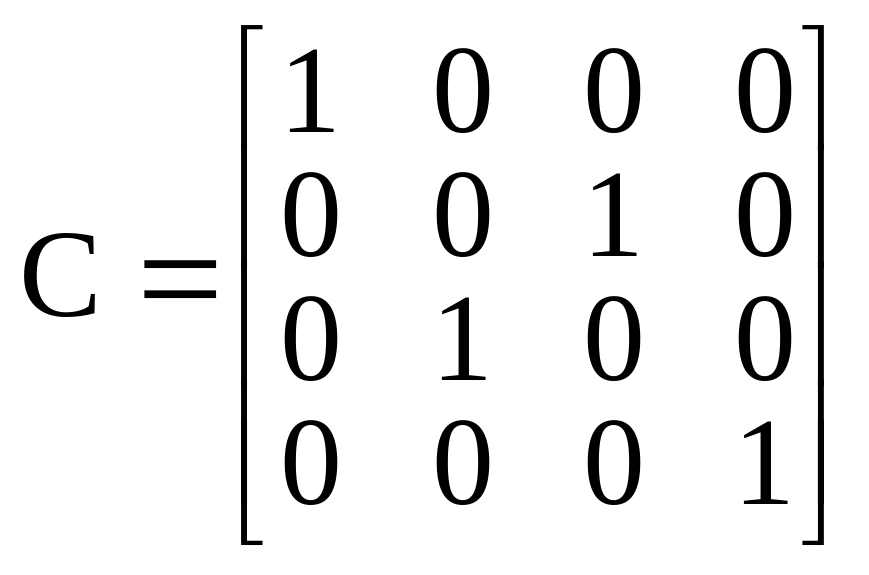Тогда матрица оператора А в «новом» базисе

.
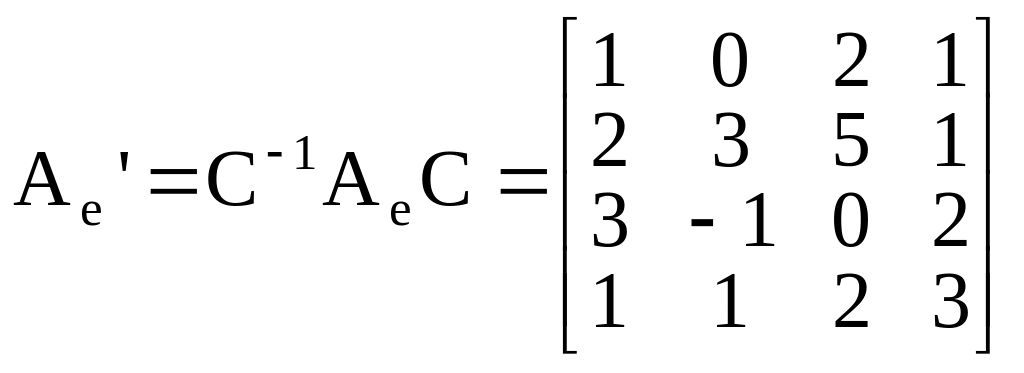