
- •Линейные операторы. Квадратичные формы
- •1. Линейные операторы. Матрица линейного оператора.
- •Определение оператора. Действия с операторами.
- •1.2. Матрица линейного оператора.
- •1.3. Задачи
- •Образ и ядро линейного оператора
- •2.1. Задачи
- •Собственные векторы и собственные значения линейного оператора
- •3.1.Оператор простой структуры.
- •3.2. Задачи
- •Инвариантные подпространства
- •4.1. Задачи
- •Каноническая форма жордана
- •5.1. Задачи.
- •Линейные операторы в евклидовых и унитарных пространствах.
- •6.1. Нормальный оператор.
- •6.2. Приведение матрицы нормального оператора к диагональному виду
- •6.3. Полярное разложение оператора
- •6.4. Задачи
- •Билинейные и квадратичные формы
- •7.1. Приведение квадратичной формы к каноническому виду
- •7.1.1. Метод Лагранжа
- •7.1.2. Метод Якоби
- •7.1.3.Приведение квадратичной формы к каноническому виду в ортонормированном базисе
- •7.1.4. Задачи
- •7.2. Знакоопределенные квадратичные формы
- •7.2.1. Матрица Грама
- •7.2.2. Критерий Сильвестра
- •7.2.3. Одновременное приведение двух квадратичных форм к каноническому виду.
- •7.2.4. Задачи
- •7.3 Поверхности второго порядка
- •7.3.1. Задачи
- •Литература
- •Содержание
- •1. Линейные операторы. Матрица линейного оператора 3
- •1.1. Определение оператора. Действия с операторами 3
4.1. Задачи
Линейный оператор А задается в базисе
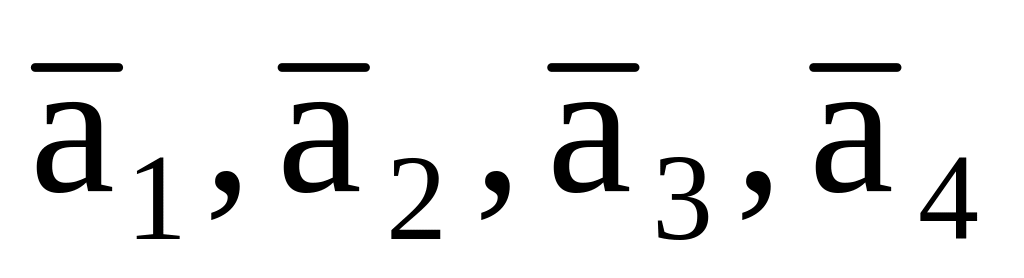
матрицей
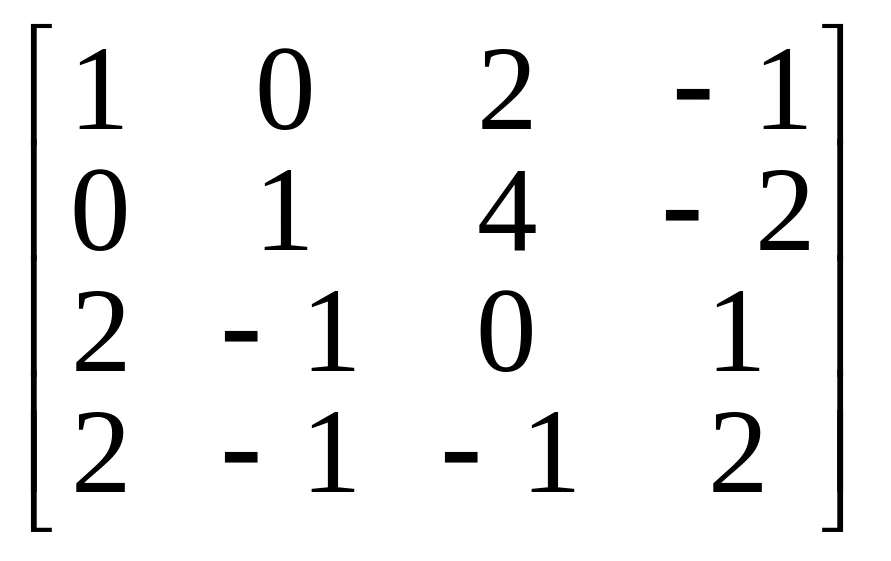 .
.
Показать,
что линейная оболочка векторов
![]() и
и
![]() является подпространством инвариантным
относительно оператора А.
является подпространством инвариантным
относительно оператора А.
2. Доказать, что линейная оболочка любой системы собственных векторов оператора А является инвариантным подпространством.
3. Найти все подпространства трехмерного пространства, инвариантные относительно оператора, заданного в некотором базисе матрицей
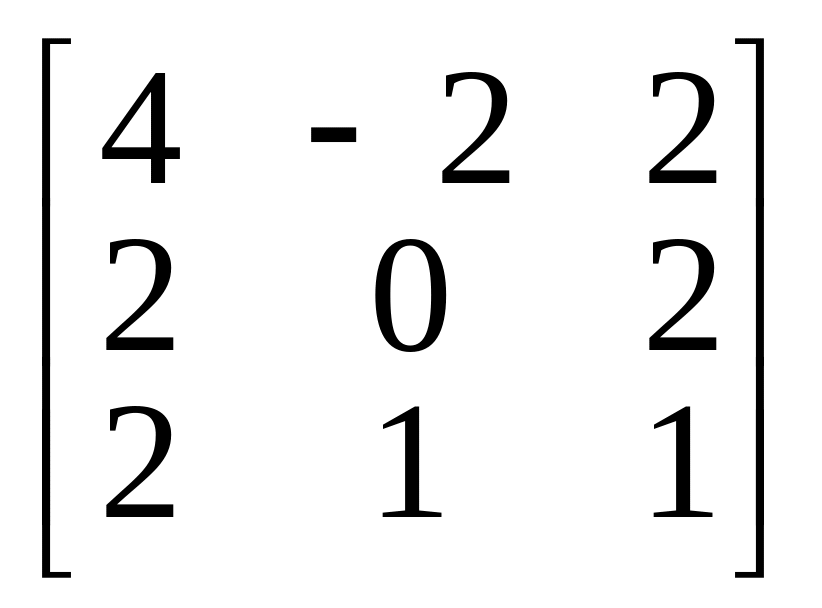 .
.
4. Найти все подпространства трехмерного пространства, инвариантные относительно двух линейных операторов, заданных матрицами
 .
.
5.
Доказать, что любое подпространство
,
инвариантное относительно невырожденного
оператора А, будет инвариантно и
относительно обратного оператора
![]() .
.
6. Пусть линейное преобразование А -мерного пространства в базисе имеет диагональную матрицу с различными элементами на диагонали. Найти все подпространства, инвариантные относительно А, и определить их число.
Каноническая форма жордана
Определение
1.
![]() -мерной
жордановой клеткой, соответствующей
числу
называется треугольная матрица вида
-мерной
жордановой клеткой, соответствующей
числу
называется треугольная матрица вида
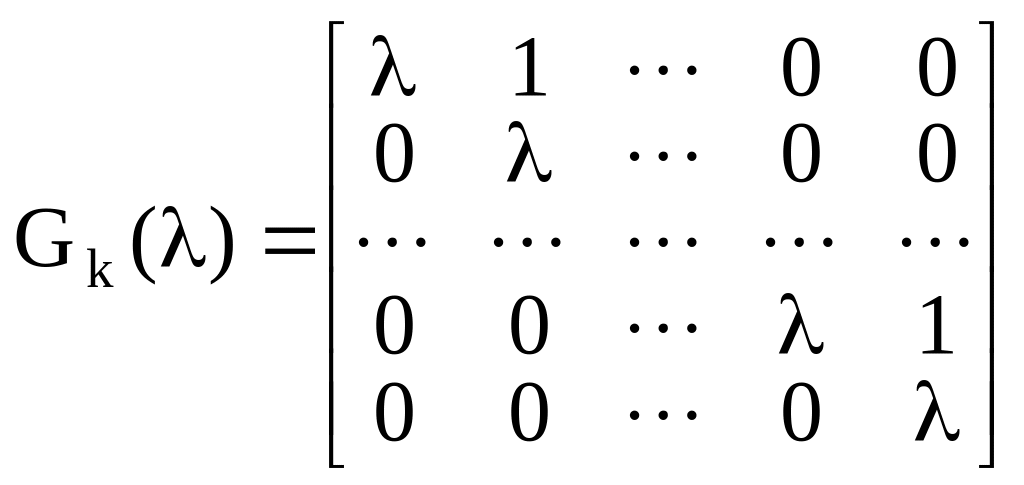 .
.
Определение 2. Говорят, что матрица линейного оператора действующего в - мерном пространстве имеет нормальную жорданову форму, если вдоль ее главной диагонали расположены жордановы клетки, а остальные элементы нули
 ,
,
где
![]() ,
а
-
собственные значения оператора. Не
исключена возможность, что в матрице
для некоторых номеров
,
а
-
собственные значения оператора. Не
исключена возможность, что в матрице
для некоторых номеров
![]() или
или
![]() .
.
Базис пространства Х, в котором матрица оператора А имеет нормальную жорданову форму, называется каноническим.
В - мерном комплексном пространстве для каждого линейного оператора А существует базис, в котором матрица имеет нормальную жорданову форму. При переходе к другому каноническому базису матрица оператора сохраняется с точностью до перестановки клеток. Нормальная жорданова форма является простейшей формой, к которой может быть приведена матрица произвольного оператора.
Построение нормальной жордановой формы состоит из следующих этапов:
1.
Составляется и решается характеристическое
уравнение
![]() ,
определяются собственные значения
оператора
и их кратности
.
,
определяются собственные значения
оператора
и их кратности
.
2.
Для каждого собственного значения
подсчитывается число соответствующих
ему жордановых клеток
![]() различной размерности
различной размерности
![]() по формуле:
по формуле:
![]()
где
![]() -
ранг матрицы
-
ранг матрицы
![]() .
Простым собственным значениям
соответствуют жордановы клетки единичной
размерности.
.
Простым собственным значениям
соответствуют жордановы клетки единичной
размерности.
3. После того, как число клеток разной размерности, соответствующих различным собственным значениям определено, записывается нормальная жорданова форма с точностью до перестановки клеток. Канонический базис при этом остается неопределенным.
Пример. Привести к нормальной жордановой форме матрицу оператора:
 .
.
Для нахождения собственных значений оператора составим и решим характеристическое уравнение
 .
.
Откуда
собственное значение
![]() и его кратность
и его кратность
![]() .
.
Определим теперь число жордановых клеток разной размерности. В нашем случае возможны три ситуации:
1. Существует три одномерных клетки.
2. Существует одна одномерная клетка и одна двумерная клетка.
3. Существует одна трехмерная клетка.
Сосчитаем число одномерных клеток:

Поэтому
количество одномерных клеток
![]() .
Следовательно, возможен только третий
вариант и нормальная жорданова форма
матрицы оператора имеет вид
.
Следовательно, возможен только третий
вариант и нормальная жорданова форма
матрицы оператора имеет вид
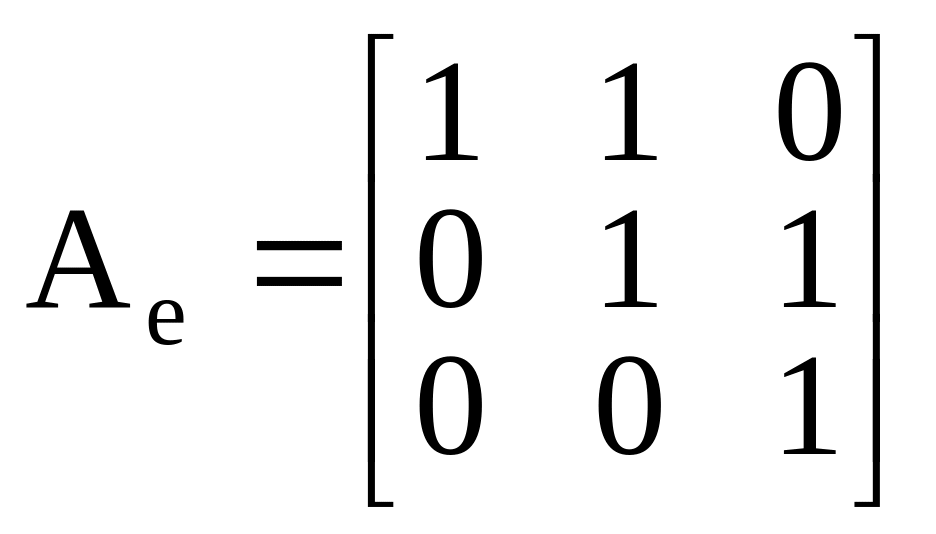 .
.
