
- •Линейные операторы. Квадратичные формы
- •1. Линейные операторы. Матрица линейного оператора.
- •Определение оператора. Действия с операторами.
- •1.2. Матрица линейного оператора.
- •1.3. Задачи
- •Образ и ядро линейного оператора
- •2.1. Задачи
- •Собственные векторы и собственные значения линейного оператора
- •3.1.Оператор простой структуры.
- •3.2. Задачи
- •Инвариантные подпространства
- •4.1. Задачи
- •Каноническая форма жордана
- •5.1. Задачи.
- •Линейные операторы в евклидовых и унитарных пространствах.
- •6.1. Нормальный оператор.
- •6.2. Приведение матрицы нормального оператора к диагональному виду
- •6.3. Полярное разложение оператора
- •6.4. Задачи
- •Билинейные и квадратичные формы
- •7.1. Приведение квадратичной формы к каноническому виду
- •7.1.1. Метод Лагранжа
- •7.1.2. Метод Якоби
- •7.1.3.Приведение квадратичной формы к каноническому виду в ортонормированном базисе
- •7.1.4. Задачи
- •7.2. Знакоопределенные квадратичные формы
- •7.2.1. Матрица Грама
- •7.2.2. Критерий Сильвестра
- •7.2.3. Одновременное приведение двух квадратичных форм к каноническому виду.
- •7.2.4. Задачи
- •7.3 Поверхности второго порядка
- •7.3.1. Задачи
- •Литература
- •Содержание
- •1. Линейные операторы. Матрица линейного оператора 3
- •1.1. Определение оператора. Действия с операторами 3
3.1.Оператор простой структуры.
Определение. Линейный оператор А, действующий в n – мерном пространстве называется оператором простой структуры, если ему соответствует ровно n линейно независимых собственных векторов. В этом случае можно построить базис пространства из собственных векторов оператора, в котором матрица оператора имеет наиболее простой диагональный вид
 ,
,
где
![]() -
собственные значения оператора. Очевидно,
что верно и обратное: если в некотором
базисе пространства Х матрица оператора
имеет диагональный вид, то базис состоит
из собственных векторов оператора.
-
собственные значения оператора. Очевидно,
что верно и обратное: если в некотором
базисе пространства Х матрица оператора
имеет диагональный вид, то базис состоит
из собственных векторов оператора.
Линейный
оператор А является оператором простой
структуры тогда и только тогда, когда
каждому собственному значению
кратности
![]() соответствует ровно
линейно независимых собственных
векторов. Так как собственные векторы
есть решения системы уравнений
соответствует ровно
линейно независимых собственных
векторов. Так как собственные векторы
есть решения системы уравнений
![]() то, следовательно, каждому корню
характеристического уравнения
то, следовательно, каждому корню
характеристического уравнения
![]() кратности
,
должна соответствовать матрица
кратности
,
должна соответствовать матрица
![]() ранга
ранга
![]() .
.
Всякая
матрица
размера
![]() ,
соответствующая оператору простой
структуры, подобна диагональной матрице
,
соответствующая оператору простой
структуры, подобна диагональной матрице
![]()
![]() ,
,
где матрица перехода Т от исходного базиса к базису из собственных векторов имеет своими столбцами вектор-столбцы из координат собственных векторов матрицы (оператора А).
Пример. Привести матрицу линейного оператора к диагональному виду
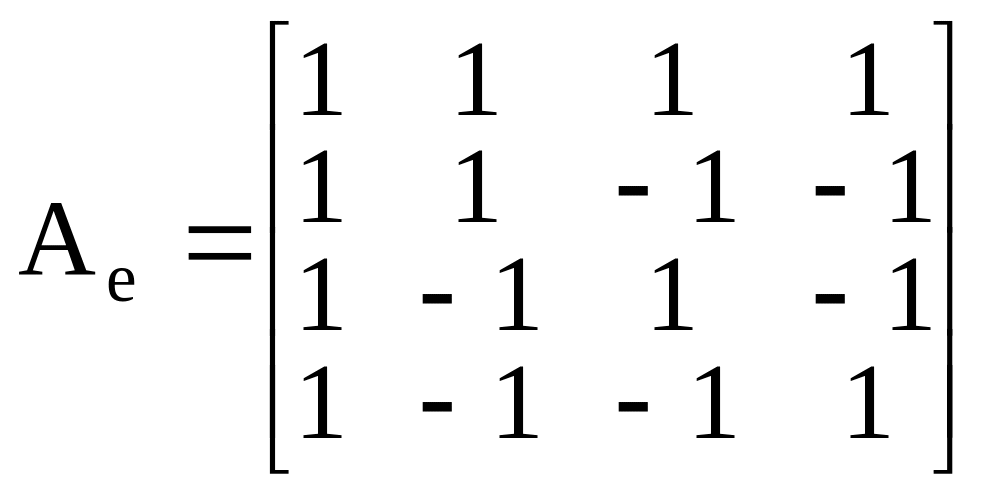 .
.
Составим характеристическое уравнение и найдем его корни.
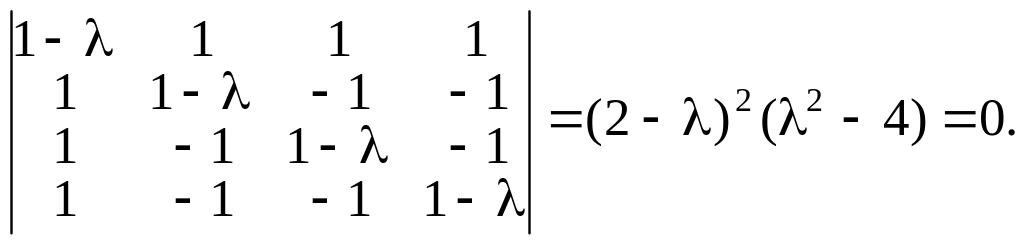
Откуда
собственные значения
![]() кратности
кратности
![]() и
и
![]() кратности
кратности
![]() .
.
Первое собственное значение . Ему соответствуют собственные векторы, координаты которых являются
решением системы
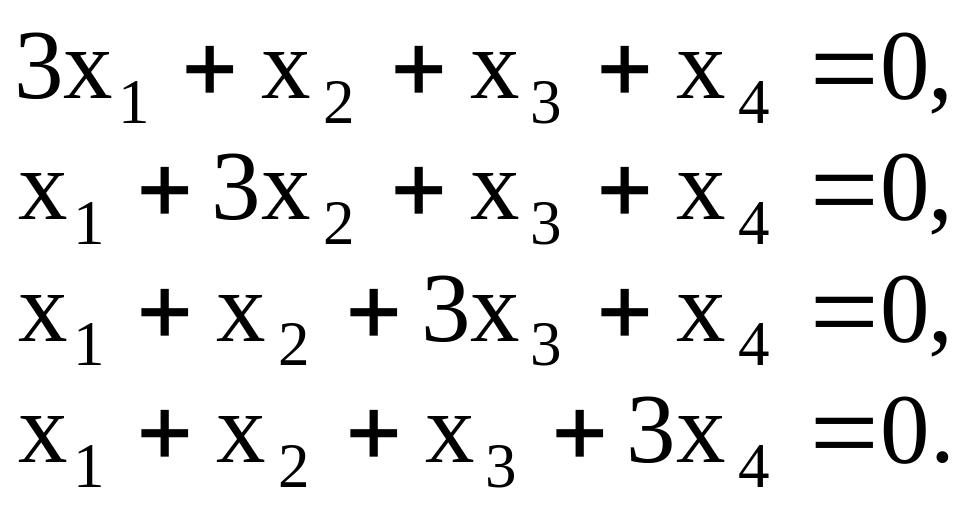
Ранг
данной системы равен 3, поэтому имеется
только одно независимое решение,
например, вектор
![]() .
.
Собственные векторы, соответствующие , определяются системой уравнений

ранг которой равен 1 и, следовательно, существует три линейно независимых решения, например,
![]() ,
,![]() ,
,![]() .
.
Таким образом, каждому собственному значению кратности соответствует ровно линейно независимых собственных векторов и, следовательно, оператор является оператором простой структуры. Матрица перехода Т имеет вид

и связь между подобными матрицами и определяется соотношением
 =
=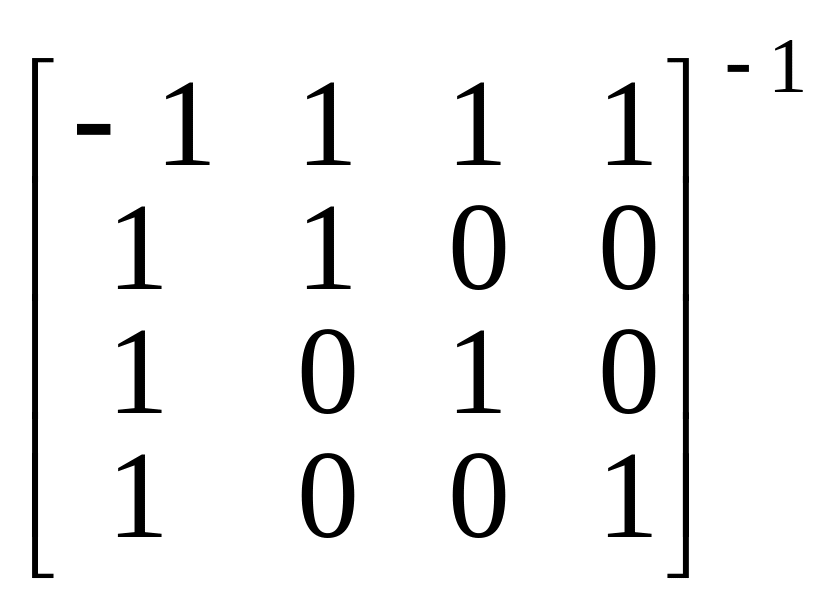

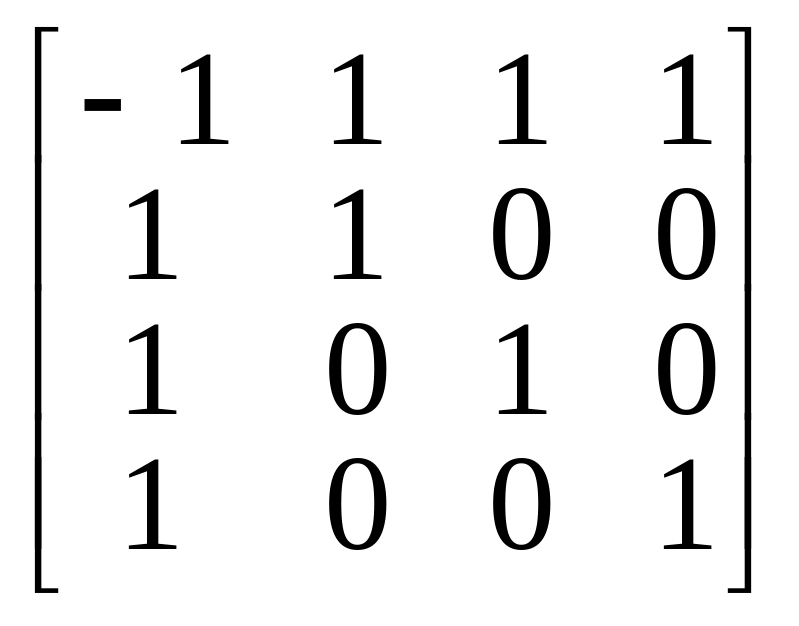 .
.
3.2. Задачи
Найти собственные векторы и собственные значения
линейных операторов, заданных в некотором базисе матрицами:
1.
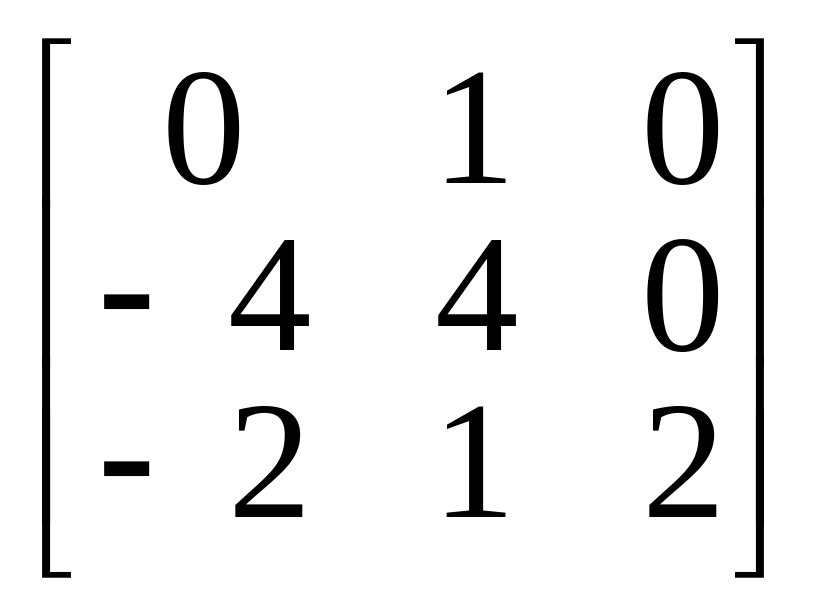 2.
2.
 3.
3.
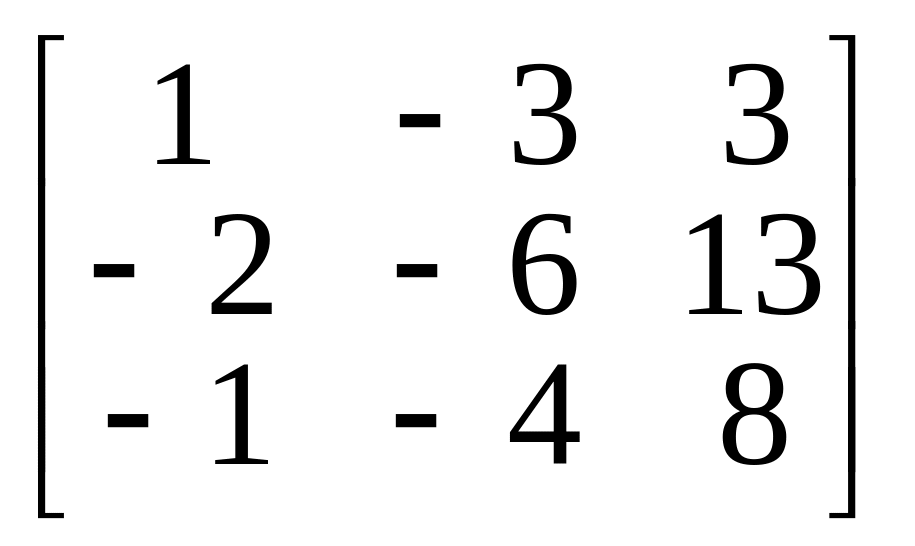
4.
 5.
5.
 6.
6.

Определить какие из следующих линейных операторов можно привести к диагональному виду путем перехода к новому базису. Найти этот базис и соответствующую ему матрицу:
7.
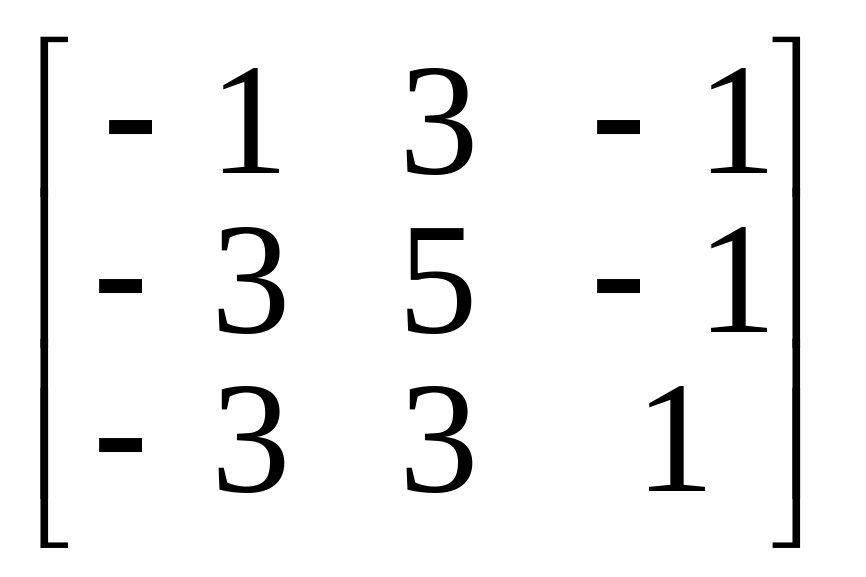 8.
8.
 9.
9.

10. Доказать, что собственные векторы линейного оператора, соответствующие различным собственным значениям линейно независимы.
11.
Доказать, что если линейный оператор
А, действующий в
![]() , имеет n
различных значений, то любой линейный
оператор В перестановочный с А, обладает
базисом собственных векторов, причем
любой собственный вектор А будет
собственным и для В.
, имеет n
различных значений, то любой линейный
оператор В перестановочный с А, обладает
базисом собственных векторов, причем
любой собственный вектор А будет
собственным и для В.
Инвариантные подпространства
Определение
1..
Подпространство L
линейного пространства X
называется инвариантным относительно
оператора А, действующего в X,
если для каждого вектора
![]() его образ
его образ
![]() также принадлежит
также принадлежит
![]() .
.
Основные свойства инвариантных подпространств определяются следующими соотношениями:
1.
Если
![]() и
и
![]() являются инвариантными подпространствами
относительно оператора А, то их сумма
являются инвариантными подпространствами
относительно оператора А, то их сумма
![]() и пересечение
и пересечение
![]() также инвариантны относительно оператора
А.
также инвариантны относительно оператора
А.
2.
Если пространство Х разлагается в прямую
сумму подпространств
и
(![]() )
и
инвариантно относительно А, то матрица
оператора в базисе, который является
объединением базисов
и
есть блочная матрица
)
и
инвариантно относительно А, то матрица
оператора в базисе, который является
объединением базисов
и
есть блочная матрица
 ,
,
где
![]() - квадратные матрицы, 0 – нулевая матрица.
- квадратные матрицы, 0 – нулевая матрица.
3. Во всяком инвариантном относительно оператора А подпространстве оператор имеет хотя бы один собственный вектор.
Пример
1. Рассмотрим
ядро
некоторого оператора А, действующего
в Х. По определению
![]() .
Пусть
.
Тогда
.
Пусть
.
Тогда
![]() ,
так как нулевой вектор содержится во
всяком линейном подпространстве.
Следовательно, ядро
- инвариантное относительно А
подпространство.
,
так как нулевой вектор содержится во
всяком линейном подпространстве.
Следовательно, ядро
- инвариантное относительно А
подпространство.
Пример 2. Пусть в некотором базисе пространства Х оператор А задается матрицей
 .
.
Определить все подпространства трехмерного пространства, инвариантные относительно А.
Проще всего задача решается в базисе, составленном из собственных векторов оператора, если такой базис существует. Поэтому найдем вначале собственные векторы А.
Составим и решим характеристическое уравнение
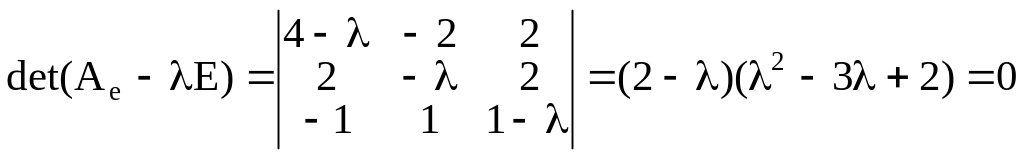 .
.
Откуда
собственные значения
![]() кратности
и
кратности
кратности
и
кратности
![]() .
Первое собственное значение простое.
Соответствующий ему собственный вектор
определяется системой уравнений
.
Первое собственное значение простое.
Соответствующий ему собственный вектор
определяется системой уравнений

решая которую получим,
например,
![]() .
.
Собственные векторы для определяются уравнением
![]() ,
,
имеющим
два линейно независимых решения,
например,
![]() и
и
![]() .
Таким образом, в нашем случае существует
базис из собственных векторов.
.
Таким образом, в нашем случае существует
базис из собственных векторов.
Пусть
теперь
![]() .
Тогда вектор
.
Тогда вектор
![]() .
Воспользовавшись теперь определением
инвариантного подпространства, получим,
что инвариантными будут следующие
подпространства:
.
Воспользовавшись теперь определением
инвариантного подпространства, получим,
что инвариантными будут следующие
подпространства:
1.
Прямая с базисным вектором
![]() .
.
2.
Прямые с базисными векторами
![]() и
и
![]() .
.
3.
Линейная оболочка векторов
![]() ,
т.е. плоскость, задаваемая уравнением
.
,
т.е. плоскость, задаваемая уравнением
.
4.
Линейные оболочки векторов
![]() и
и
![]() .
.
5. Все трехмерное пространство и нулевое пространство.
