Линейная корреляция двух переменных
.docЛинейная корреляция двух переменных
Методические указания
Цель работы: Закрепить понятие линейной корреляционной зависимости; научиться оценивать количественную тесноту связи с помощью коэффициента корреляции, составлять уравнение регрессии.
Краткие сведения из теории.
Метеорологические величины и явления, как правило, обусловлены большим числом факторов, полный учет которых практически невозможен, а в большинстве случаев и нецелесообразен. Поэтому при установлении причинно-следственных связей ограничивается лишь теми факторами, которые на основании общих физических соображений могут рассматриваться как главные. Эти главные факторы и определяют основной вид связи, а менее существенные причины создают поле рассеяния, характерное для стохастических (вероятностных) зависимостей.
Последние являются обобщением понятия статистических или корреляционных связей, соответствующим не выборочным статистическим или вариационным рядам, а полной совокупности рассматриваемых случайных величин, когда объем совокупности «n» стремится к бесконечности или к конечному числу N, охватывающему весь диапазон изменения случайной величины.
В климатологии и синоптической метеорологии при решении практических задач имеют дело со значительными по объему выборками из некоторой генеральной совокупности: следовательно, в практике исследований обычно рассматриваются не стохастические, а статистические или корреляционные связи. Т.е. такие связи, когда численному значению одной величины соответствует несколько значений (совокупность) другой величины.
Простейшим видом зависимости являются линейные корреляционные связи между переменными. В случае нелинейности связи между метеорологическими величинами, как правило, путём простейших преобразований можно привести их к линейному виду. Например, используя кусочно-линейную функцию.
Далее рассматривается только линейная корреляция двух переменных величин. Числовым критерием степени близости корреляционной зависимости к функциональной в случае линейной связи является коэффициент корреляции – r.
Существует несколько формул для определения коэффициента корреляции. Приведем наиболее распространенные из них:
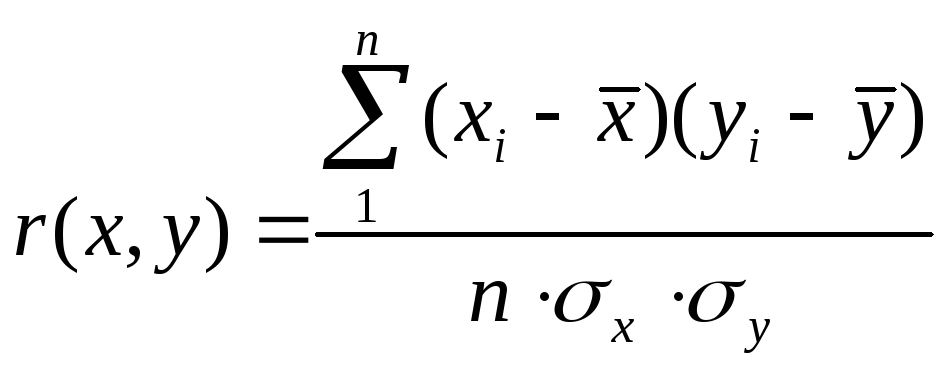
![]()
где
![]() ,
xi, yi
– соответственно средние арифметические
и возможные значения рядов x
и y.
,
xi, yi
– соответственно средние арифметические
и возможные значения рядов x
и y.
σx и σy
– их средние квадратические отклонения
или
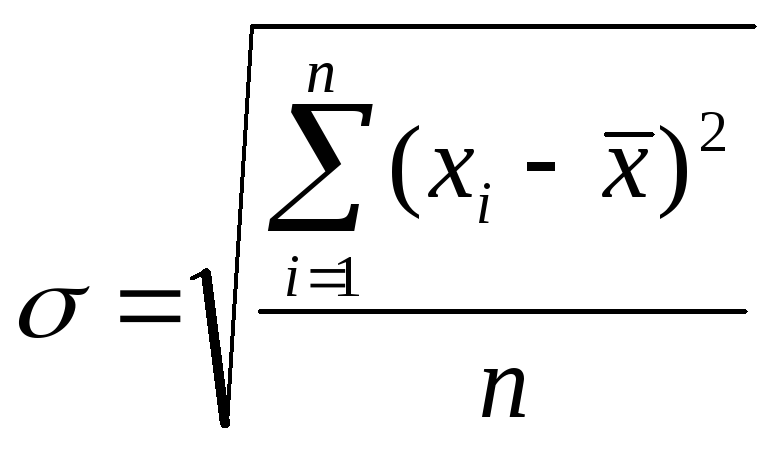
![]() - ковариация или второй смешанный момент
связи величин x, y.
- ковариация или второй смешанный момент
связи величин x, y.
Еще одна формула для расчета коэффициента
корреляции -
![]() .
.
Свойства коэффициента корреляции.
1. Величина коэффициента корреляции не изменится, если из всех значений ряда Х и ряда Y вычесть какие-либо постоянные а и b, а полученные результаты разделим на k и l. Иначе говоря, если вместо переменных «х» и «y» введем новые
![]() и
и
![]()
Тогда r(x,y)=r(x',y').
Это свойство позволяет во многих случаях упростить расчет коэффициента корреляции.
2. Коэффициент может принимать значение от -1 до +1. Если коэффициент корреляции положителен – это говорит о прямой корреляционной зависимости (положительному приращению одного аргумента соответствует положительное приращение другого). Если отрицателен - зависимость обратная (положительному приращению одного аргумента соответствует отрицательное приращение другого).
3. При наличии линейной функциональной
зависимости между величинами коэффициент
корреляции r = ±1. Чем ближе
r к единице, тем теснее
линейная корреляция между величинами
«х» и «y». На практике
принято считать что если
![]() <
0.5 – зависимость слабая, 0.7>
<
0.5 – зависимость слабая, 0.7>![]() >0.5
– умеренная, если
>0.5
– умеренная, если
![]() >0.7
– сильная. Но можно говорить о связи и
при меньших r, если её
можно объяснить физически.
>0.7
– сильная. Но можно говорить о связи и
при меньших r, если её
можно объяснить физически.
Для предварительного выяснения линейности связи можно построить графическое изображение связи в прямоугольной (декартовой) системе координат, нанося точки с координатами (xi, yi).
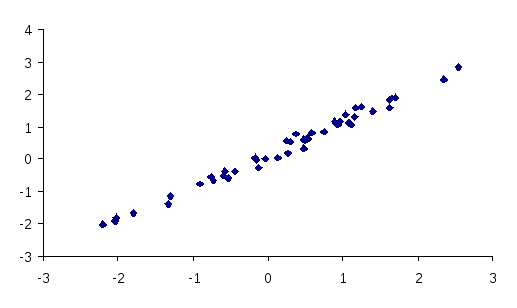
r=0.97
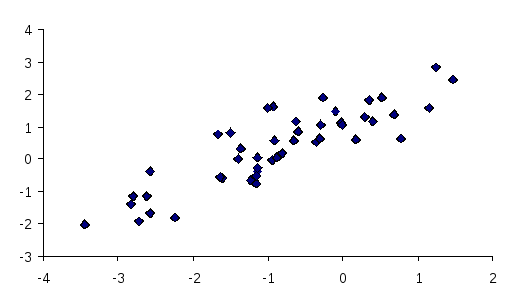

r=0.84
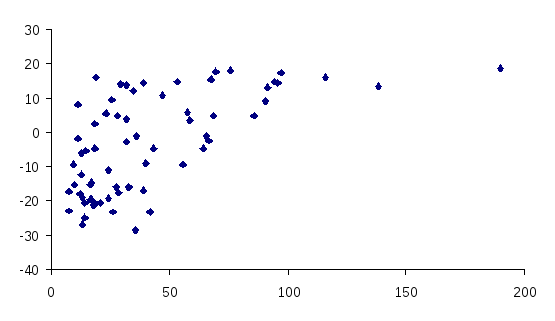
r=0.61
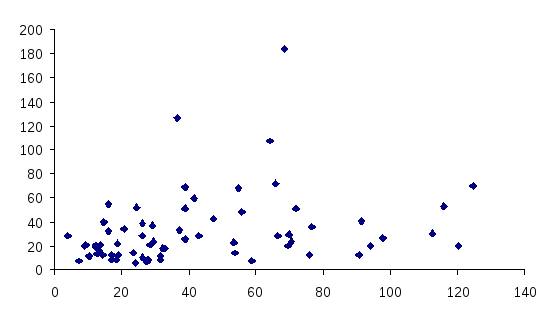
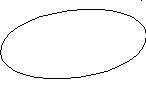
r=0.27
Рисунок 1 - Пример положительной корреляционной зависимости для разных r.
Графическое изображение связи, кроме установления формы зависимости позволяет также увидеть тесноту связи. Если полученное поле корреляции представляет эллипс, большая ось которого в 2 раза и более превышает малую, существует хорошая линейная зависимость (r>0.6). Если корреляционного поле близко к кругу, линейная зависимость слабая или совсем отсутствует.
Оценка точности коэффициента корреляции.
В результате метеорологических наблюдений мы всегда получаем некоторую ограниченную совокупность данных, представляющих собой выборку из генеральной совокупности. Все параметры, которые мы получаем из выборки (в том числе и коэффициент корреляции) лишь приближенно характеризуют параметры генеральной совокупности. Они могут меняться от выборки к выборке. Поэтому нужно знать отличие выборочных коэффициентов корреляции и коэффициентов регрессии от их величин в генеральной совокупности. В математической статистике имеется положение, что с вероятностью, близкой к единице, можно утверждать, что при достаточно большом объеме выборки n выборочный коэффициент линейной корреляции будет мало отличаться от такого же в генеральной совокупности.
Средняя квадратическая ошибка выборочного коэффициента корреляции mr оценивается по формуле:
![]()
Зная статистическую ошибку коэффициента корреляции, можно найти доверительные интервалы r в генеральной совокупности по формуле:
![]()
где tst – критерий Стьюдента, определяется в зависимости от числа степеней свободы ν=n-2 и уровня надежности (Р) по таблице. (Таблица 1 приложение 1)
Зная критерий Стьюдента (tst), можно также определить достоверность выборочного коэффициента корреляции достоверен, если выполняется неравенство
![]()
Считается также, что если
этом коэффициент корреляции r
превышает свою среднюю ошибку σr
больше чем в 3 раза, т.е. если
![]() то он считается Значимым,
а связь реальной.
то он считается Значимым,
а связь реальной.
Отдельно нужно рассчитывать значимость полученных результатов для малых выборок. Так например, при п < 30 значимость коэффициента корреляции проверяется на основе критерия Стыодента. Для этого рассчитывается фактическое (расчетное) значение критерия
![]()
которое сопоставляется, с tтабл, определяемым по Приложению ,9 для числа степеней свободы v=п- 2 и заданного уровня значимости (обычно α = 0,05).
Если tфакт>tтабл коэффициент корреляции r считается значимым, а связь — реальной.
Если tфакт<tтабл, то считается, что связь между x и у отсутствует и значение г, отличное от нуля, получено случайно.
Также коэффициент корреляции определяется из малой выборки (n<50) оценивают коэффициент корреляции с помощью критерия Фишера:
![]()
Вычислив F, определяют его статистическую погрешность
![]()
Найдя отношение
![]() ,
получаем, что значение коэффициента
корреляции достоверно (не случайно),
если:
,
получаем, что значение коэффициента
корреляции достоверно (не случайно),
если:
![]()
Задания по работе
Изучить теорию линейной корреляции двух переменных, и ответить устно на следующие вопросы:
-
Какие виды зависимости вы знаете?
-
Что такое корреляционная зависимость?
-
Как оценить тесноту линейной зависимости двух переменных?
-
Что такое ковариация?
-
Какие свойство коэффициента корреляции вы знаете?
-
Как определить статистическую ошибку коэффициента корреляции? Для чего она определяется?
-
Когда для оценки корреляции используют критерий Фишера?
Произвести расчеты по предложенным данным. Дать характеристику зависимости. Объяснить её физически. Оценить статистическую значимость результатов.
Отчет по лабораторной работе должен содержать результаты расчетов и грамотно изложенный анализ зависимостей.
Распределение Стьюдента
|
ν |
Р |
||
|
0,95 |
0,99 |
0,999 |
|
|
16 |
2,12 |
2,92 |
4,01 |
|
18 |
2,10 |
2,88 |
3,92 |
|
20 |
2,09 |
2,85 |
3,85 |
|
22 |
2,07 |
2,82 |
3,79 |
|
24 |
2,06 |
2,80 |
3,75 |
|
26 |
2,06 |
2,78 |
3,71 |
|
28 |
2,05 |
2,76 |
3,67 |
|
30 |
2,04 |
2,75 |
3,65 |
|
40 |
2,02 |
2,7 |
3,55 |
|
60 |
2,00 |
2,66 |
3,46 |
|
120 |
1,98 |
2,62 |
3,37 |
|
∞ |
1,98 |
2,58 |
3,29 |
Выполнение в программе Exel.
При
решении различных задач в Excel
можно использовать,
как в формулах, так и независимо,
встроенные функции. На панели Стандартные
с
помощью кнопки
![]() Вставка
функции откроем
диалоговое окно мастера
функций,
которое содержит
13 различных категорий функций.
Вставка
функции откроем
диалоговое окно мастера
функций,
которое содержит
13 различных категорий функций.
Категория Статистические является одной из самых многочисленных. Она содержит 78 статистик (функций обрабатываемых данных). Среди них есть интересующая нас функция КОРРЕЛ.
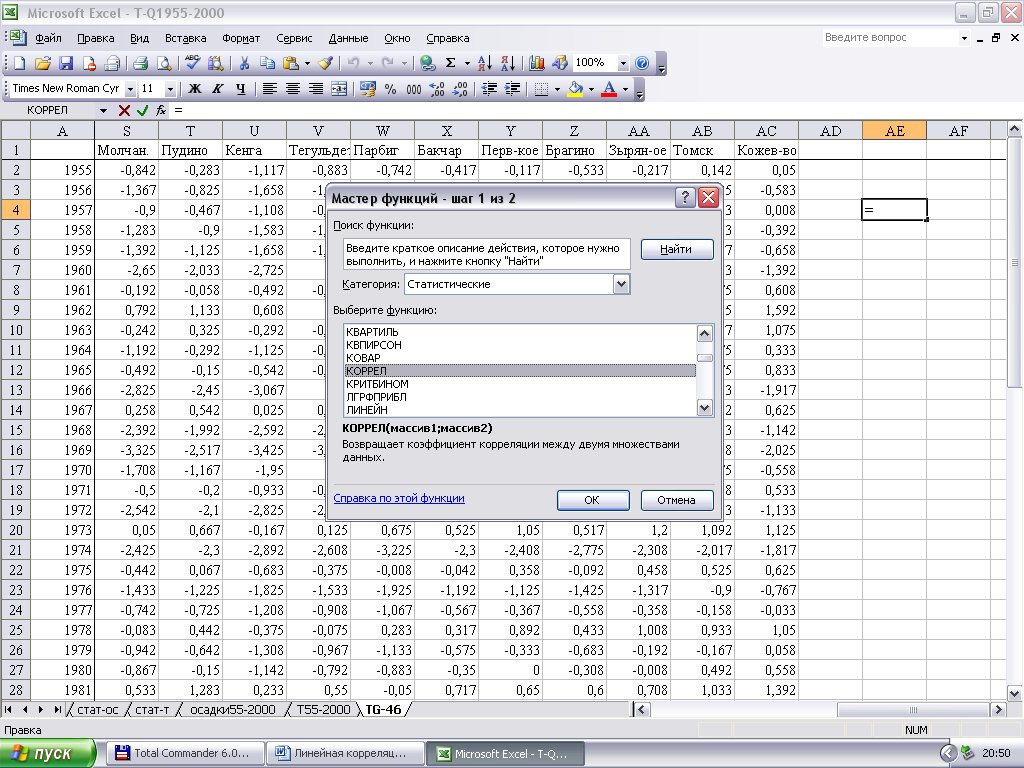
Диалоговое окно которой выглядит следующим образом. С помощью мыши вы выделяете интересующие вас ряды данных для анализа парной корреляции. Отдельно вводится первый массив данных и отдельно второй. В диалоговом окне сразу отображается результат расчетов парной корреляционной функции.
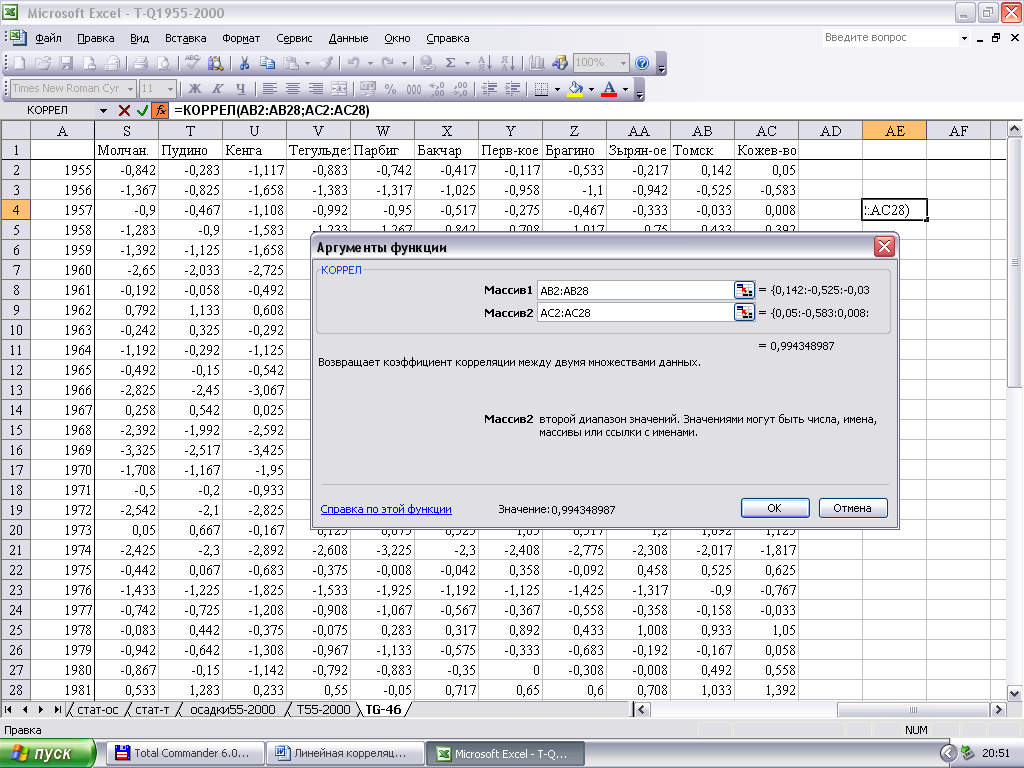
Оценка достоверности результатов.
Для проверки существенности различий используем статистику t-Стьюдента с (n-1) степенью свободы. Рассчитываем по формуле tфакт.
Для того, чтобы вызвать табличное значение критерия Стьюдента tтабл воспользуемся функцией СТЬЮДРАСПОБР, диалоговое окно которой показано на рисунке. Число степеней не показано, чтобы не вводить вас в заблуждение. Оно вычисляется как ν=n-2 и просто указывается в виде числа. Вероятность в этой функции предусмотрено указывать обратную, т.е. если вы проверяете значимость с 95% вероятностью выполнения, то указываете в диалоговом окне обратную разность в долях единицы Р=1-0,95=0,05. Можно воспользоваться и таблицей из приложения 1. Далее сравниваете полученное расчетное значение и табличное и делаете вывод.