7.1. Приведение квадратичной формы к каноническому виду

Основная задача, связанная с квадратичными формами, состоит в приведении ее с помощью линейного невырожденного преобразования переменных (преобразования базиса) к максимально простому (каноническому) виду.

Определение 2. Каноническим видом эрмитовой квадратичной формы называется выражение вида

,

где - координаты вектора , а - вещественные канонические коэффициенты.

7.1.1. Метод Лагранжа

Метод Лагранжа позволяет привести к каноническому виду симметрическую вещественную квадратичную форму. Идея метода состоит в последовательном дополнении квадратного многочлена по каждой переменной до полного квадрата.

Пусть

.

Будем считать, что . Если это не так, то возможны два варианта:

1. Какой–нибудь из . Тогда перенумеровав базисные векторы (переобозначение переменных), получим требуемое условие.

2. Если все , и, например, , то сделаем следующее невырожденное преобразование

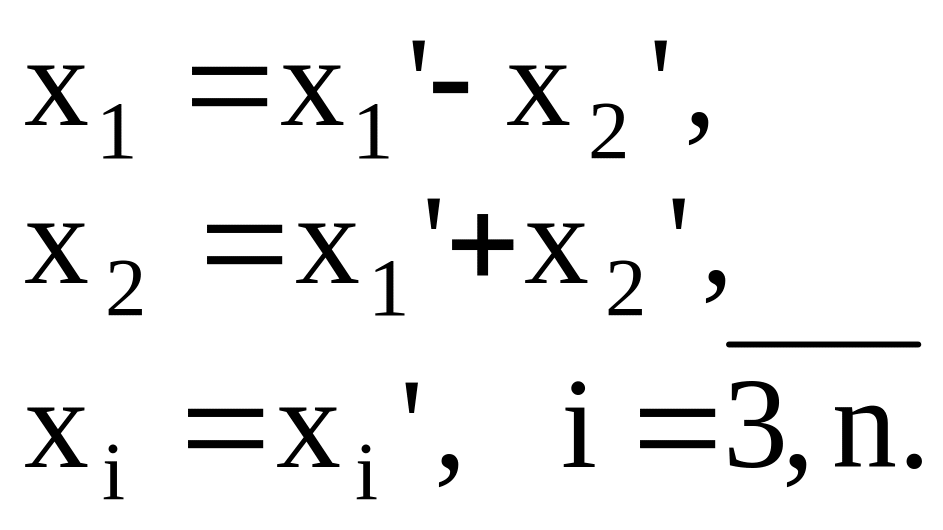
При этом и коэффициент при .

Выделим в выражении для слагаемые, содержащие :

.

Преобразуем слагаемые с :

.

Сделаем невырожденное преобразование переменных

,

.

Обозначим . Тогда для получим

.

Если теперь квадратичная форма

,

то приведена к каноническому виду. Если , то, проводя аналогичные преобразования координат , за конечное число шагов приведем квадратичную форму к каноническому виду.

Пример. Приведем к каноническому виду квадратичную форму

.

Здесь все , а коэффициент . Поэтому сделаем преобразование

Тогда

.

Выделим и преобразуем слагаемые с :

.

Сделаем замену переменных

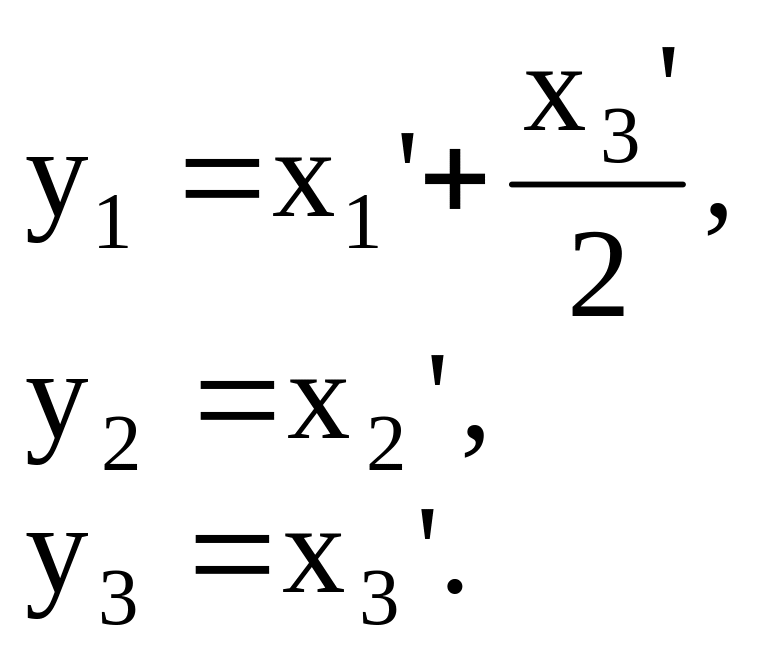
Тогда

.

Преобразуем далее слагаемые с :

и сделаем замену переменных

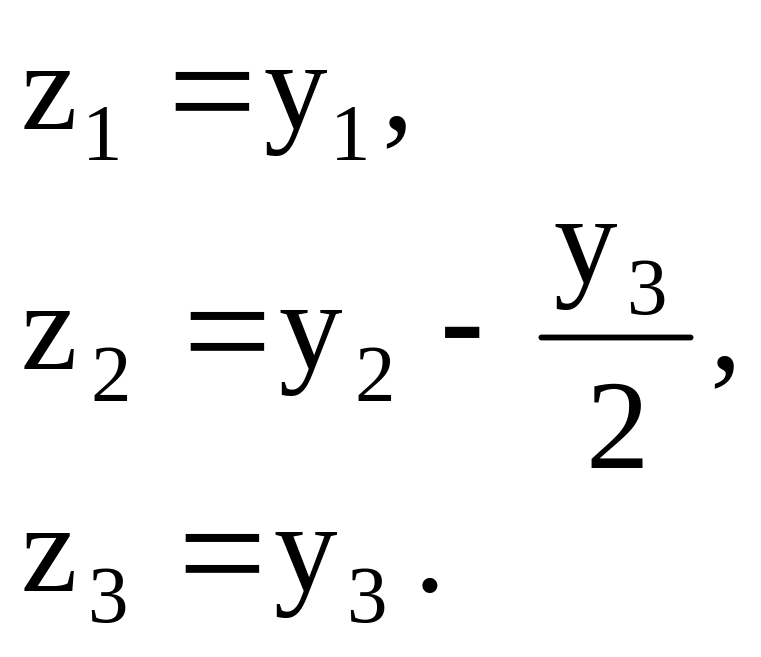
Квадратичная форма принимает канонический вид

.

7.1.2. Метод Якоби

Метод Якоби позволяет найти канонические коэффициенты невырожденной эрмитовой квадратичной формы по ее коэффициентам в произвольном базисе, не строя сам канонический базис.

Обозначим через главный минор - го порядка матрицы квадратичной формы , т. е.

.

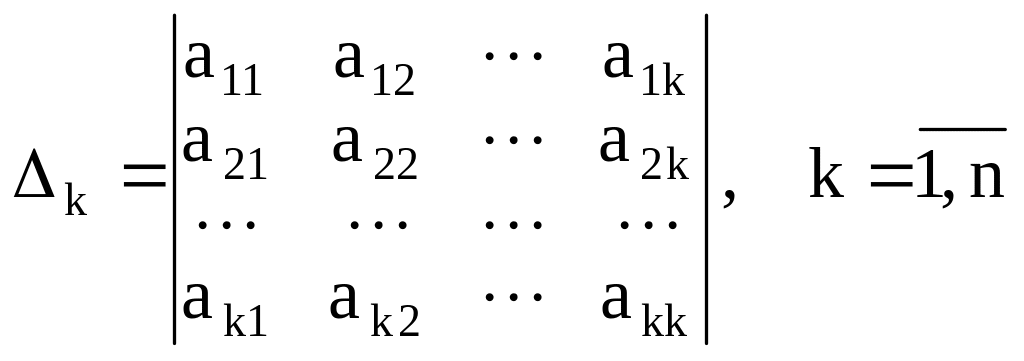Если все главные миноры матрицы квадратичной формы отличны от нуля, то существует канонический базис, в котором данная форма имеет вид

,

где

.

Пример. Приведем к каноническому виду методом Якоби квадратичную форму

.

Матрица квадратичной формы

.

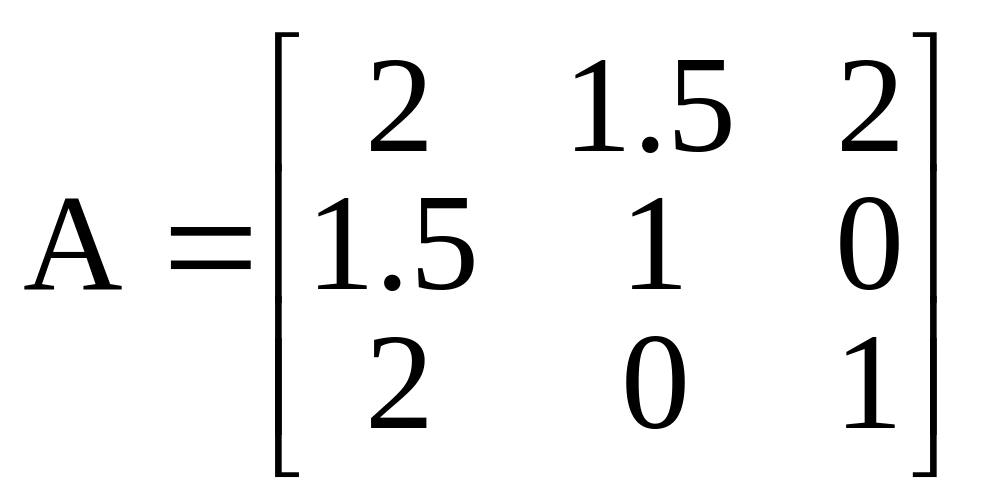Главные миноры матрицы

.

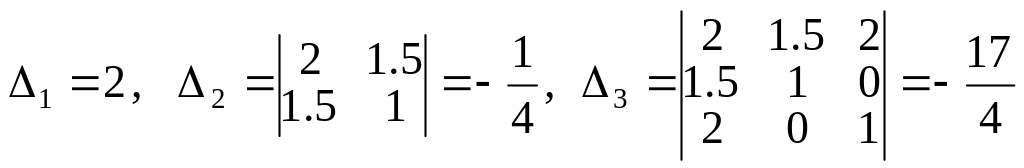Поэтому

,

где - координаты вектора в каноническом базисе.

7.1.3.Приведение квадратичной формы к каноническому виду в ортонормированном базисе

Пусть - эрмитова квадратичная форма, заданная в унитарном (евклидовом) пространстве. С помощью некоторого невырожденного линейного преобразования она может быть приведена к каноническому виду, причем выбор канонического базиса неоднозначен. Оказывается, что для эрмитовой квадратичной формы среди всех канонических базисов существует и ортонормированный базис.

Так как - матрица квадратичной формы является эрмитовой (самосопряженной), то она представима в виде

,

где - собственные значения, а - ортонормированная матрица собственных векторов матрицы А. Введем новые переменные (новые координаты вектора ) соотношениями

.

В новых переменных квадратичная форма

.

Таким образом, для приведения квадратичной формы к каноническому виду необходимо найти собственные значения матрицы А, которые и являются каноническими коэффициентами. Если нужна также связь между старыми и новыми координатами вектора , то нужно найти ортонормированную матрицу собственных векторов.

Пример. Найдем канонический вид в ортонормированном базисе квадратичной формы

.

Матрица квадратичной формы

.

Для определения канонических коэффициентов составим и решим характеристическое уравнение

.

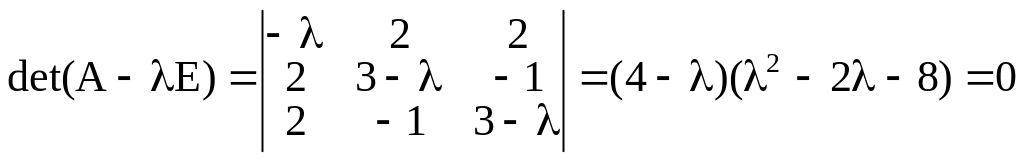Откуда , и канонический вид квадратичной формы

.

Найдем связь между старыми и новыми координатами вектора . Собственные векторы матрицы А при определяются уравнением

,

линейно независимые решения которого, например, векторы

.

Координаты третьего собственного вектора определяются системой

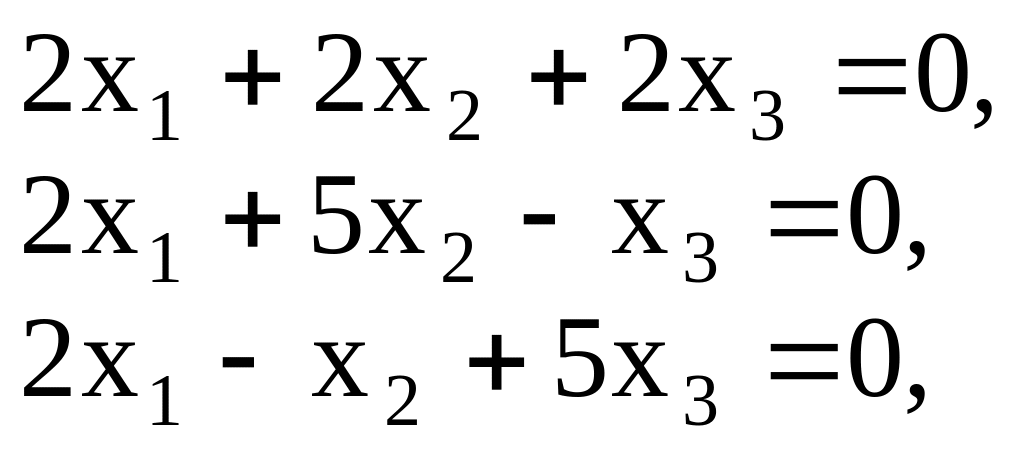
которая имеет решение . Применяя к полученным векторам процесс ортогонализации Грама - Шмидта, получим искомый ортонормированный базис

,

и связь между старыми и новыми координатами вектора