
- •Линейные операторы. Квадратичные формы
- •1. Линейные операторы. Матрица линейного оператора.
- •Определение оператора. Действия с операторами.
- •1.2. Матрица линейного оператора.
- •1.3. Задачи
- •Образ и ядро линейного оператора
- •2.1. Задачи
- •Собственные векторы и собственные значения линейного оператора
- •3.1.Оператор простой структуры.
- •3.2. Задачи
- •Инвариантные подпространства
- •4.1. Задачи
- •Каноническая форма жордана
- •5.1. Задачи.
- •Линейные операторы в евклидовых и унитарных пространствах.
- •6.1. Нормальный оператор.
- •6.2. Приведение матрицы нормального оператора к диагональному виду
- •6.3. Полярное разложение оператора
- •6.4. Задачи
- •Билинейные и квадратичные формы
- •7.1. Приведение квадратичной формы к каноническому виду
- •7.1.1. Метод Лагранжа
- •7.1.2. Метод Якоби
- •7.1.3.Приведение квадратичной формы к каноническому виду в ортонормированном базисе
- •7.1.4. Задачи
- •7.2. Знакоопределенные квадратичные формы
- •7.2.1. Матрица Грама
- •7.2.2. Критерий Сильвестра
- •7.2.3. Одновременное приведение двух квадратичных форм к каноническому виду.
- •7.2.4. Задачи
- •7.3 Поверхности второго порядка
- •7.3.1. Задачи
- •Литература
- •Содержание
- •1. Линейные операторы. Матрица линейного оператора 3
- •1.1. Определение оператора. Действия с операторами 3
5.1. Задачи.
Привести к нормальной жордановой форме матрицы линейных операторов:
1.
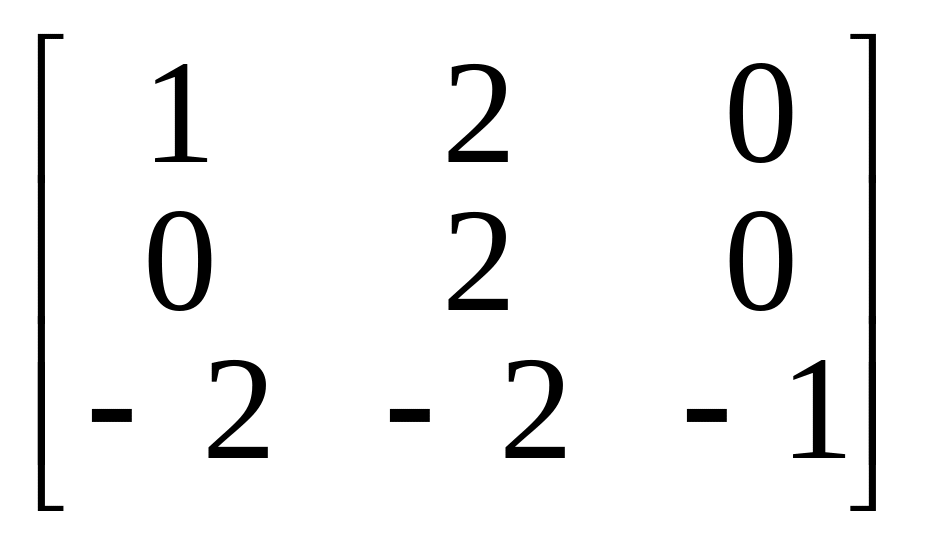 .
2.
.
2.
 .
3.
.
3.
 .
.
4.
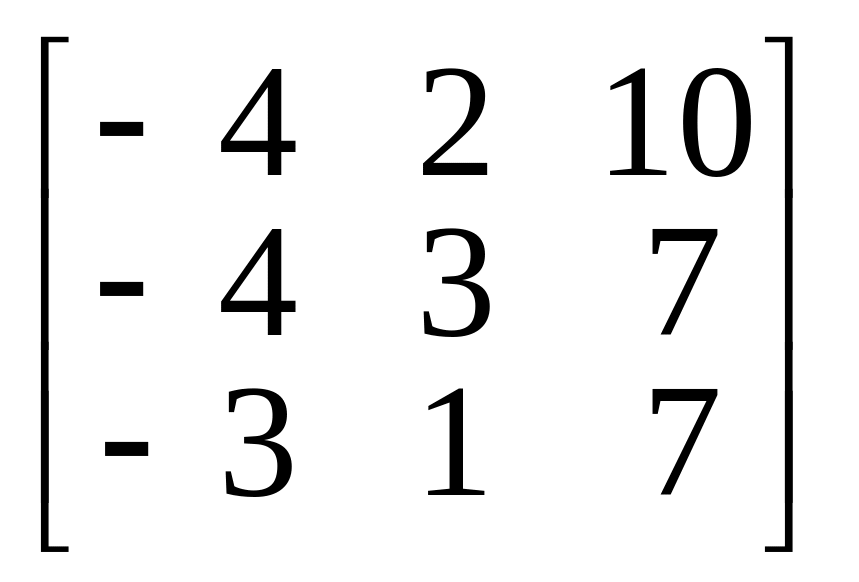 .
5.
.
5.
 .
6.
.
6.
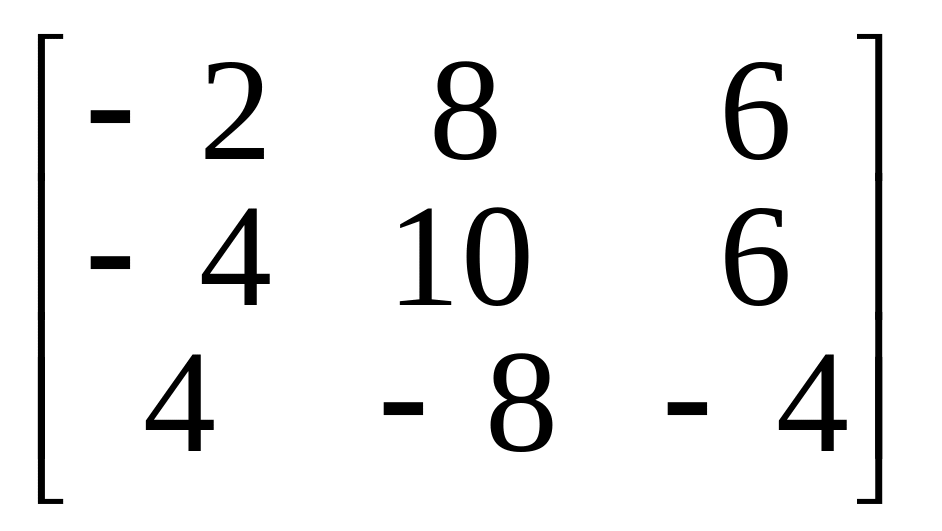 .
.
7.
 .
8.
.
8.
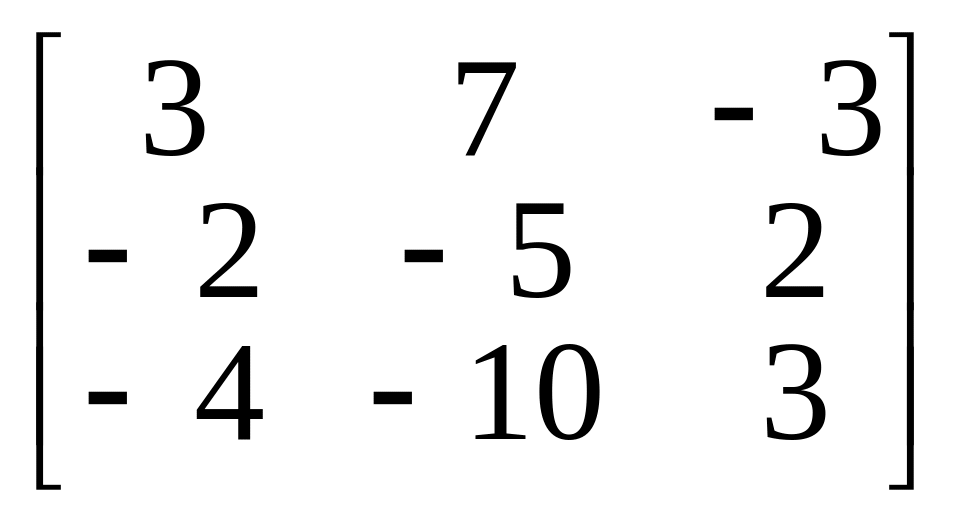 .
9.
.
9.
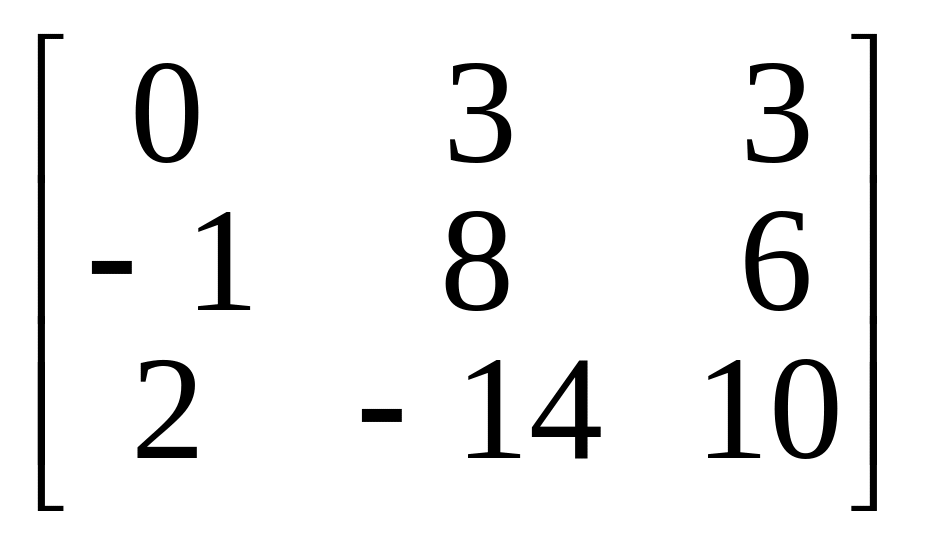 .
.
Линейные операторы в евклидовых и унитарных пространствах.
6.1. Нормальный оператор.
Наличие ортонормированного базиса в унитарном пространстве и базиса из собственных векторов линейного оператора имеют принципиальное значение при выполнении различных исследований. Поэтому основной задачей при рассмотрении линейных операторов в унитарных пространствах является изучение того класса операторов, которые в унитарном пространстве имеют ортонормированный базис из собственных векторов.
Определение
1. Пусть
![]() - произвольное унитарное пространство
и
- произвольное унитарное пространство
и
![]() - операторы, действующие в
.
Оператор
- операторы, действующие в
.
Оператор![]() называется сопряженным к линейному
оператору А, если
называется сопряженным к линейному
оператору А, если
![]() ,
,
где
![]() - скалярное произведение вектора
на вектор
- скалярное произведение вектора
на вектор
![]() .
.
Для всякого линейного оператора А существует единственный линейный сопряженный оператор . Их матрицы в любом ортонормированном базисе пространства связаны соотношением
![]() .
.
Определение 2. Линейный оператор А, действующий в , называется нормальным, если он перестановочен со своим сопряженным оператором, т. е.
![]() .
.
Оказывается, что оператор А имеет ортонормированный базис из собственных векторов тогда и только тогда, когда он является нормальным. При этом ортонормированные системы собственных векторов операторов А и совпадают, а собственные значения, соответствующие одному и тому же собственному вектору, комплексно сопряжены.
Частными случаями нормальных операторов являются:
1.Унитарный
оператор, для
которого
![]() или
или![]() .
Оператор
является унитарным тогда и только тогда,
когда
.
Оператор
является унитарным тогда и только тогда,
когда
![]() .
.
Все собственные значения унитарного оператора по модулю равны 1. Всякая ортонормированная система векторов пространства переводится унитарным оператором в ортонормированную систему векторов. Матрица унитарного оператора удовлетворяет условию
![]() .
.
Такие матрицы называются унитарными.
В
случае вещественного евклидова
пространства
![]() и матрица унитарного (ортонормированного)
оператора удовлетворяет соотношению
и матрица унитарного (ортонормированного)
оператора удовлетворяет соотношению
![]() .
.
Таким образом, столбцы данной матрицы ортонормированны. Например, ортонормированной матрицей второго порядка является следующая матрица
![]() .
.
2. Самосопряженный оператор. Этот оператор совпадает со своим сопряженным, т. е.
![]() .
.
Матрица самосопряженного оператора удовлетворяет условию
![]() .
.
Такие матрицы называются эрмитовыми. Все собственные значения самосопряженного оператора вещественны.
В случае евклидова пространства самосопряженный оператор переходит в симметричный оператор, матрица которого является симметричной, т. е.
![]() .
.
Определение 3. Самосопряженный оператор Н называется положительно (неотрицательно) определенным, если
![]() .
.
Всякий
самосопряженный оператор положительно
определен тогда и только тогда, когда
его собственные значения положительны.
Для любого оператора А операторы
![]() и
и
![]() являются неотрицательно определенными.
являются неотрицательно определенными.
6.2. Приведение матрицы нормального оператора к диагональному виду
Так как для всякого нормального оператора существует ортонормированный базис из собственных векторов, то матрица всякого нормального оператора может быть приведена к диагональному виду соотношением
![]() .
.
Все отличие от общего случая состоит в том, что теперь матрица перехода С (матрица из координат собственных векторов) должна быть выбрана так, чтобы ее столбцы были ортонормированны, т. е. теперь С – унитарная матрица. Тогда общее соотношение перепишется в виде
![]()
Полезно помнить, что всякий матричный многочлен
![]()
от матрицы имеет те же собственные векторы, что и матрица , а соответствующие собственные значения равны
![]() .
.
Например, матрица
 .
.
Пример. Найти ортонормированный базис из собственных векторов и матрицу в этом базисе для линейного оператора, заданного в некотором ортонормированном базисе матрицей
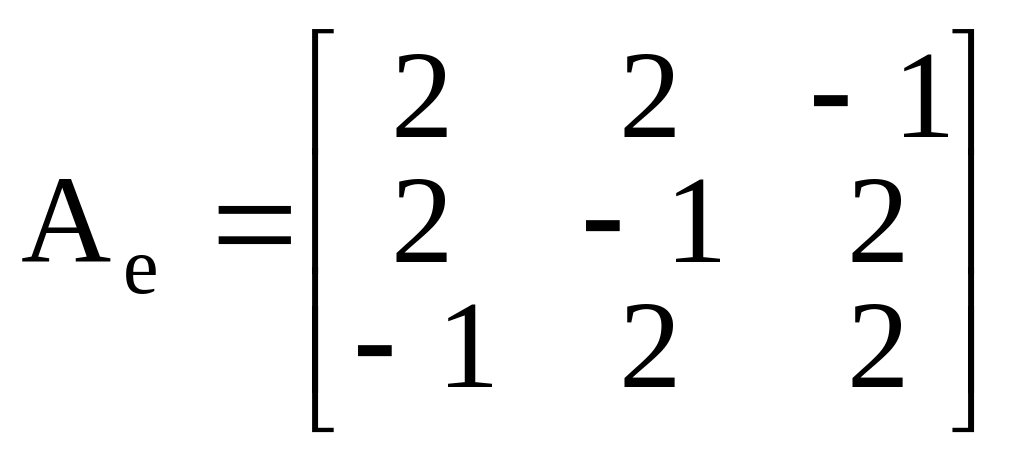 .
.
Матрица является симметричной, поэтому искомый базис заведомо существует. Для нахождения собственных значений составляем и решаем характеристическое уравнение
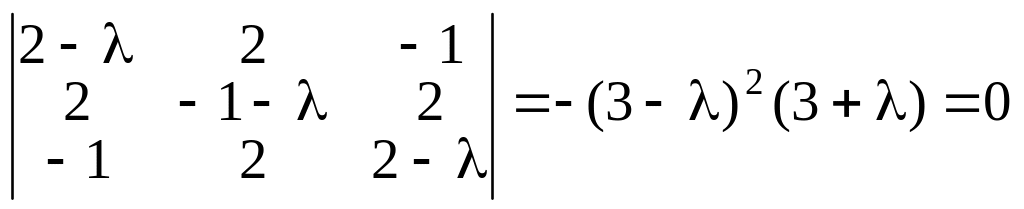 ,
,
откуда
собственные значения
![]() кратности
и
кратности
и
![]() кратности
кратности
![]() .
Поэтому диагональная матрица оператора
в базисе из собственных векторов
.
Поэтому диагональная матрица оператора
в базисе из собственных векторов
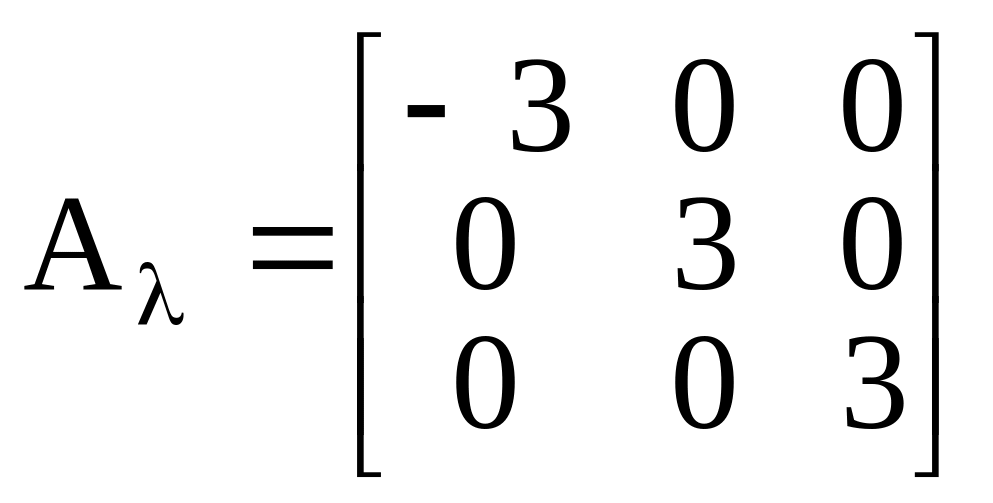 .
.
Для
нахождения базиса составляем и решаем
системы уравнений
![]() .
При
имеем
.
При
имеем

Нормированное решение этой системы вектор
![]() .
.
При имеем
![]() .
.
Линейно независимые решения этого уравнения
![]() .
.
Применяя
к векторам
![]() процедуру ортогонализации Грама–Шмидта,
получим еще два ортонормированных
собственных вектора
процедуру ортогонализации Грама–Шмидта,
получим еще два ортонормированных
собственных вектора
![]() .
.
Тогда матрица перехода С имеет вид
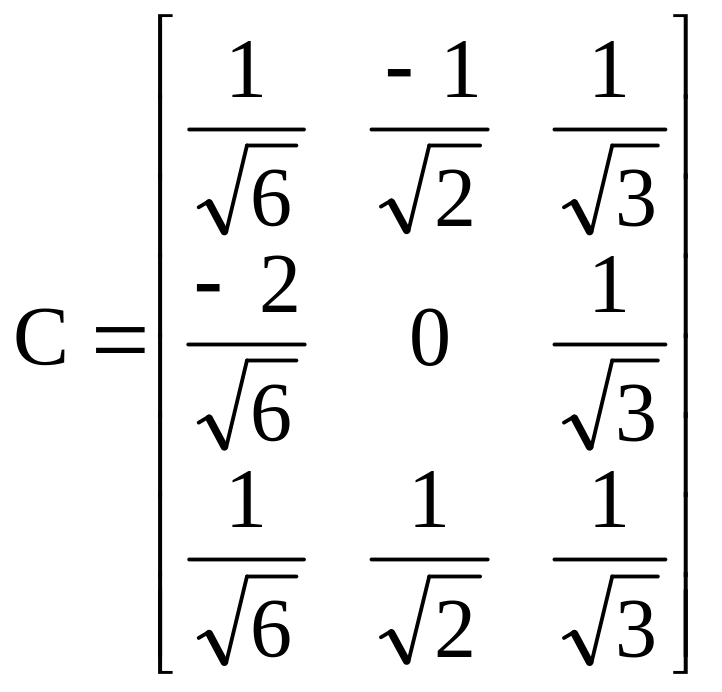 .
.
