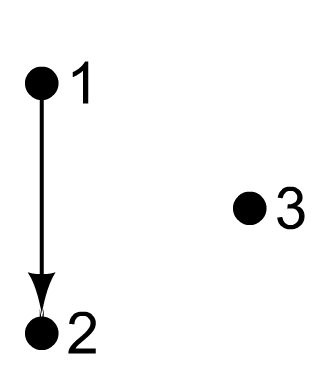Орієнтовані графи та бінарні відношення

Твердження 11. Нехай V – непорожня множина. Тоді між множиною орграфів з множиною вершин V та множиною бінарних відношень, заданих на множині V, існує взаємно однозначна відповідність.

Доведення. Нехай задано орграф G=(V,E). Побудуємо на множині V бінарне відношення R_G таким чином: xR_Gy  (x,y)E.

Нехай на непорожній множині V задано бінарне відношення R. Побудуємо орграф G_R таким чином: за множину вершин орграфу візьмемо множину V, а за множину дуг – множину {(u,v)| <u,v>R}.

Наведені правила побудови бінарного відношення за орграфом та орграфу за бінарним відношенням визначають бієкцію множини орієнтованих графів з множиною вершин V на множину бінарних відношень, заданих на множині V. Твердження доведено.

Розглянемо приклади. Нехай задано орграф G=({1,2,3,4},{(1,1),(1,3), (2,3),(3,4)}). Побудуємо відношення R_G на множині V. Для цього перегля-немо дуги орграфу G. Відношення R_G має вигляд: R_G={<1,1>,<1,3>, <2,3>,<3,4>}. Нехай тепер на множині {1,2,3,4} задано бінарне відношення R={<3,2>,<4,2>,<4,1>,<2,1>,<2,4>}. Це відношення можна подати у вигляді такого орграфу: G_R=({1,2,3,4},{(3,2),(4,2),(4,1),(2,1),(2,4)}).

Поняття орієнтованого дерева

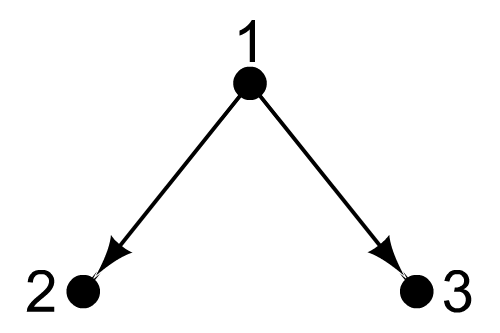
Орієнтованим деревом називається орграф без напівконтурів, у якому існує вершина (коренева вершина, або корінь), з якої досяжна будь-яка інша вершина цього орграфу. Наприклад, орграф на рис.18,а є орієнтованим деревом, бо він не має напівконтурів, а з вершини 1 досяжні вершини 2 та 3. Орграф на рис.18,б також є орієнтованим деревом, оскільки у ньому немає напівконтурів, а з вершини 3 досяжні вершини 1 та 2. Орграф на рис.18,в не є орієнтованим деревом, тому що має напівконтур 1,2,3,1. Орграф на рис.18,г не є орієнтованим деревом, тому що з жодної його вершини не досяжні усі інші. З цієї ж причини не являється орієнтованим деревом й орграф на рис.18,д.

а)	б)	в)	г)	д)
		Рис. 18

Піддеревом орієнтованого дерева Т називається підграф дерева Т, який є орієнтованим деревом. Нехай Т=(V,E) – орієнтоване дерево, vV. Вершина v визначає піддерево Т_v=(V_v,E_v) орієнтованого дерева Т, множина вершин якого (V_v) складається з вершини v та усіх досяжних з v вершин, а E_v= ={(u,w)|u,wV_v, (u,w)E}.

Розглянемо приклад. Нехай задано орієнтоване дерево Т=({1,2,3,4,5, 6,7,8},{(1,2),(1,3),(1,4),(2,5),(3,6),(3,7),(5,8)}). Вершина 2 визначає піддерево Т₂=({2,5,8},{(2,5),(5,8)}), вершина 3 – піддерево Т₃=({3,6,7}, {(3,6),(3,7)}), вершина 4 – піддерево Т₄=({4},).

Нехай T=(V,E) – орієнтоване дерево, (u,v)E. Вершина u називається батьком вершини v, а вершина v – сином вершини u (або дочірньою вершиною вершини u). Вершина u орієнтованого дерева Т називається листком, якщо on(u)=0. Наприклад, у орієнтованому дереві ({1,2,3,4},{(1,2),(2,3),(2,4)}) вершини 3 та 4 є листками, вершина 1 являється батьком вершини 2, а вершина 2 – батьком вершин 3 та 4, вершина 2 є сином вершини 1, вершини 3 та 4 є дочірніми для вершини 2.

Орієнтоване дерево називається упорядкованим, якщо множина дочірніх вершин кожної його вершини упорядкована.

Орграф називається бінарним, якщо для будь-якої його вершини v on(v)2. Бінарний орграф, що є орієнтованим деревом, називається бінарним деревом. Прикладом бінарного дерева є орграф Т=({1,2,3,4,5,6},{(1,2),(1,3),(2,4), (2,5),(3,6)}). Обчислимо для кожної вершини v орграфу Т напівстепінь виходу on(v) й переконаємося, що on(v)2: on(1)=2, on(2)=2, on(3)=1, on(4)=0, on(5)=0, on(6)=0.

Нехай Т=(V,E) – орієнтоване дерево, vV. Глибиною вершини v (позначається d(v)) називається довжина шляху між коренем Т та вершиною v. Висотою вершини v (позначається h(v)) називається довжина найдовшого шляху між v та листком Т, досяжним з v. Висотою орієнтованого дерева Т (позначається h_Т) називається висота вершини, що є коренем Т. Рівнем вершини v (позначається l(v)) називається величина h_Т - d(v).

Нехай, наприклад, задано орієнтоване дерево Т=({1,2,3,4,5,6},{(1,2), (1,3),(3,4),(3,5),(4,6)}). Обчислимо висоту Т. Для цього потрібно визначити висоту кореня Т. Коренем Т є вершина 1, листки Т – вершини 2,5,6. Для кожного листка Т побудуємо шлях між коренем й цим листком. Маємо: 1,2 – шлях між 1 та 2; 1,3,5 – шлях між 1 та 5; 1,3,4,6 – шлях між 1 та 6. Найдовшим з цих трьох шляхів є шлях між 1 та 6; його довжина дорівнює трьом, отже, h(1)=h_T=3. Аналогічно визначимо висоту кожної з некорене-вих вершин. Маємо: h(2)=h(5)=h(6)=0, h(3)=2, h(4)=1. Визначимо глибину кожної з вершин Т. Маємо: d(1)=0, d(2)=d(3)=1, d(4)=d(5)=2, d(6)=3. Об-числимо рівень кожної з вершин Т: l(1)=h_T -d(1)=3-0=3, l(2)=h_T -d(2)=3-1=2, l(3)=h_T -d(3)=3-1=2, l(4)=h_T -d(4)=3-2=1, l(5)=h_T -d(5)=3-2=1, l(6)=h_T -d(6)=3-3=0.

Бінарне дерево Т називається повним, якщо існує невід’ємне ціле число k таке, що для будь-якої вершини u бінарного дерева Т, глибина якої дорівнює k, on(u)=0, а для кожної вершини v, глибина якої менша k, on(v)=2. З даного означення випливає, що усі листки повного бінарного дерева мають однакову глибину, а напівстепінь виходу кожної вершини, що не є листком, дорівнює двом. Прикладом повного бінарного дерева є орграф Т=({1,2,3,4,5,6,7},{(1,2),(1,3),(2,4),(2,5),(3,6),(3,7)}). Обчислимо глибину кожної вершини Т: d(1)=0, d(2)=1, d(3)=1, d(4)=d(5)=d(6)=d(7)=2. Обчислимо напівстепінь виходу кожної вершини Т: on(1)=on(2)=on(3)=2, on(4)=on(5)=on(6)=on(7)=0. Отже, для кожної вершини Т глибини два напівстепінь виходу дорівнює нулю, а напівстепінь виходу кожної вершини, глибина якої менша двох, дорівнює двом. Таким чином, Т є повним бінарним деревом. Бінарне дерево ({1,2,3,4}, {(1,2),(2,3),(2,4)}) не є повним, оскільки напівстепінь виходу вершини 1, яка не є листком, не дорівнює двом (on(1)=1).