- •2.1. Система управління запасами без дефіциту
- •2.2. Система управління запасами з лінійними витратами
- •2.3. Система управління запасами з дефіцитом
- •1) Алгоритм аналітичного розв’язання
- •Алгоритм чисельного розв’язання
- •3) Алгоритм розв’язання для неявно заданої системи рівнянь
- •2.4. Система управління запасами з обмеженою інтенсивністю поповнення запасів
- •2.5. Загальна детермінована модель системи управління запасами
- •2.6. Система управління запасами з оптовими знижками цін
- •Контрольні запитання
1) Алгоритм аналітичного розв’язання
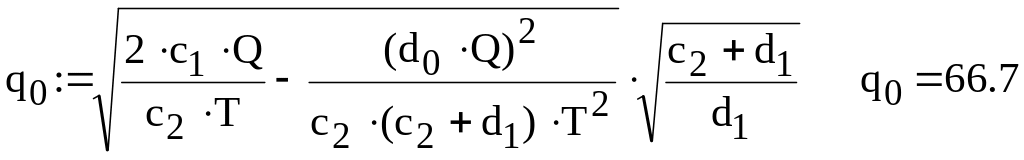
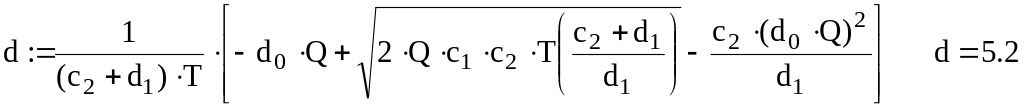
![]()
Алгоритм чисельного розв’язання
![]()
![]()
![]()
![]()
![]()
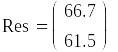
3) Алгоритм розв’язання для неявно заданої системи рівнянь
![]()
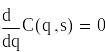
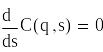
![]()
![]()
![]()
![]()
![]()
![]() грош. од.
грош. од.
![]()
Точка замовлення для фіктивного рівня запасів
![]()
![]() – найбільше ціле число
– найбільше ціле число
![]() .
.
Точка замовлення для рівня чистого запасу
![]()
Оскільки величини
і
![]() дискретні, то для визначення їх оптимальних
значень можна застосувати алгоритм, у
якому множина значень функції
дискретні, то для визначення їх оптимальних
значень можна застосувати алгоритм, у
якому множина значень функції
![]() перетворюються у двовимірний масив
(матрицю) Z.
Мінімальне значення
знаходиться за допомогою функції Mathcad
min(Z),
а значення
і
визначаються за індексами мінімального
елемента масиву Z.
перетворюються у двовимірний масив
(матрицю) Z.
Мінімальне значення
знаходиться за допомогою функції Mathcad
min(Z),
а значення
і
визначаються за індексами мінімального
елемента масиву Z.
Фрагмент алгоритму у Mathcad
![]()
![]()
![]()
![]()
![]()
Фрагмент матриці
|
|
Рис. 2.4. Графік функції
![]() грош. од.
грош. од.
Індекси мінімального елемента
![]() масиву
масиву
![]()
![]()
![]()
![]()
![]()
Мінімальне значення цільової
функції за знайденими
![]()
![]() грош. од.
грош. од.
Як видно, цей алгоритм дає такий же результат, що і попередній, але він дозволяє побудувати двовимірний графік цільової функції у вигляді графіка масиву Z.
Коментар.
За одержаними результатами можна зробити
наступний висновок:
оптимальна політика управління запасами
полягає у замовленні поставок на
поповнення запасів в обсязі
![]() одиниць товару і підтримки рівня запасу
в
одиниць товару і підтримки рівня запасу
в
![]() одиниць. Мінімальні витрати системи
складатимуть
одиниць. Мінімальні витрати системи
складатимуть
![]() грош. од. у рік. ▲
грош. од. у рік. ▲
Модель 4. Модель з втратою незадовільнених замовлень
У попередній моделі припускалось, що усі вимоги, які надходять у систему, коли в ній відсутній запас, ставляться на облік. Тепер розглянемо випадок втрати замовлень, тобто випадок, коли замовлення, які надходять в момент дефіциту запасу, назавжди втрачаються (рис.2.5) Якщо замовлення, які надходять при відсутності запасу, втрачаються, то твердження, що максимізація середнього річного доходу приводить до тієї ж стратегії функціонування, що і мінімізація середніх річних витрат, стає невірним. Доход буде залежати від тривалості стану дефіциту у системі і, отже, від стратегії функціонування. Однак можна показати, що при відповідному визначенні витрат у наслідок дефіциту запасів мінімізація середніх річних витрат дає ті ж результати, що і максимізація середнього річного прибутку.
Введемо позначення:
Q – загальний обсяг споживання
товару протягом періоду
![]() ;
;
розмір партії поповнення запасу;
P – середній річний прибуток системи;
p – продажна вартість одиниці товару (ціна);
![]() закупівельна вартість (ціна)
одиниці товару;
закупівельна вартість (ціна)
одиниці товару;
![]() –
збитки у наслідок втрати
замовлення;
–
збитки у наслідок втрати
замовлення;
![]() довжина циклу поповнення
запасів;
довжина циклу поповнення
запасів;
– час, протягом якого для деякого циклу спостерігається дефіцит запасу;
![]() – частка часу, протягом якого
у системі спостерігається дефіцит.
– частка часу, протягом якого
у системі спостерігається дефіцит.
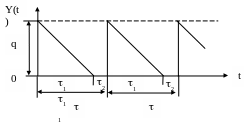
Рис. 2.5. Графік зміни рівня запасу
Середній річний прибуток дорівнює
![]() ,
(2.26)
,
(2.26)
де
![]() –
збитки у наслідок втрати замовлень, без
врахування втраченого прибутку.
–
збитки у наслідок втрати замовлень, без
врахування втраченого прибутку.
Величина
![]() представляє собою річний
прибуток, який був би одержаний, якщо б
у системі завжди був відсутній дефіцит.
Цей прибуток не залежить від стратегії
функціонування. Таким чином, якщо
записати, що
представляє собою річний
прибуток, який був би одержаний, якщо б
у системі завжди був відсутній дефіцит.
Цей прибуток не залежить від стратегії
функціонування. Таким чином, якщо
записати, що
![]() ,
то тоді мінімізація середніх річних
витрат дасть ту ж стратегію функціонування,
що і максимізація середнього річного
прибутку. Ці два вирази будуть відрізнятись
тільки на величину
,
яка не залежить від стратегії
функціонування.
,
то тоді мінімізація середніх річних
витрат дасть ту ж стратегію функціонування,
що і максимізація середнього річного
прибутку. Ці два вирази будуть відрізнятись
тільки на величину
,
яка не залежить від стратегії
функціонування.
Повернемось до позначень витрат у попередніх моделей. Тоді
![]() – витрати на створення запасу;
– витрати на створення запасу;
![]() – витрати на утримання запасів
(І – коефіцієнт витрат утримання
запасів).
– витрати на утримання запасів
(І – коефіцієнт витрат утримання
запасів).
Задача у даному випадку полягає у визначені оптимального обсягу поставки q і тривалості циклу дефіциту u.
Для будь-якого розміру
замовлення
довжина циклу дорівнює
![]() .
.
Оскільки у середньому за рік
відбувається
![]() циклів і витрати на утримання запасів
за цикл дорівнюють
циклів і витрати на утримання запасів
за цикл дорівнюють
![]() а витрати у наслідок втрати замовлень
за цикл дорівнюють
а витрати у наслідок втрати замовлень
за цикл дорівнюють
![]() то середні річні витрати дорівнюють
то середні річні витрати дорівнюють
![]() .
(2.27)
.
(2.27)
Необхідна умова того, щоб
![]() були оптимальними, полягає у тому, щоб
вони задовольняли рівнянням:
були оптимальними, полягає у тому, щоб
вони задовольняли рівнянням:
![]()
![]() ,
,
або
![]() (2.28)
(2.28)
![]() (2.29)
(2.29)
при умові
![]()
Розв’язуючи перше рівняння відносно q, одержуємо
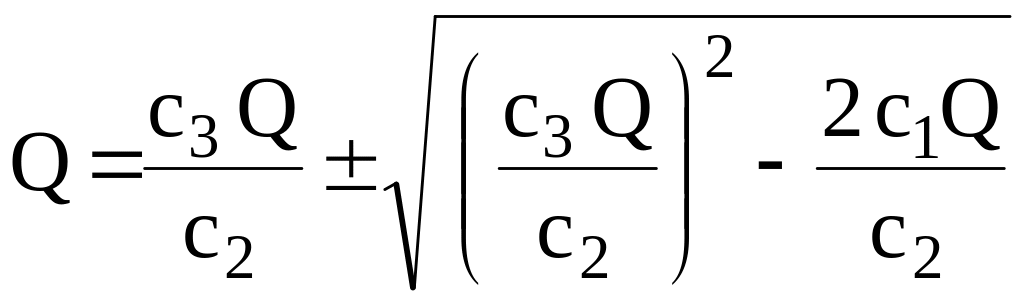 (2.30)
(2.30)
Якщо
![]() ,
то не існує дійсних значень
q,
які задовольняють (2.28). Якщо
,
то не існує дійсних значень
q,
які задовольняють (2.28). Якщо
![]() то існує єдине додатне значення q,
яке задовольняє (2.28). Коли
то існує єдине додатне значення q,
яке задовольняє (2.28). Коли
![]() ,
то є два
додатних значення
q,
які задовольняють (2.28), оскільки у цьому
випадку
,
то є два
додатних значення
q,
які задовольняють (2.28), оскільки у цьому
випадку
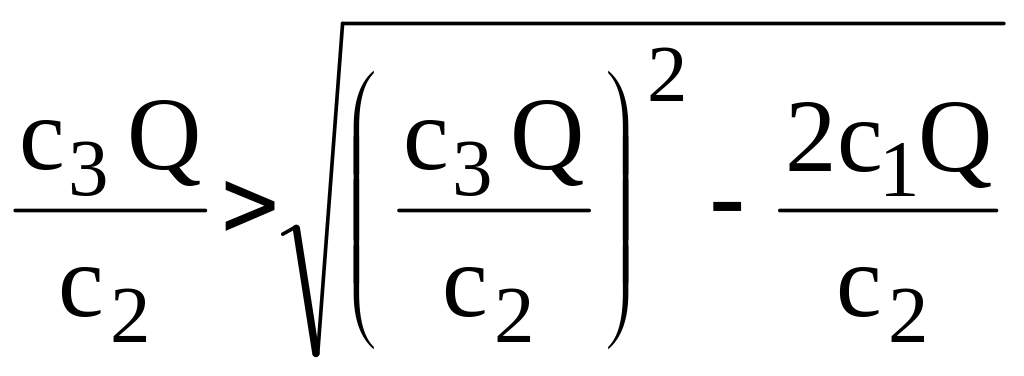 .
(2.31)
.
(2.31)
У випадку, якщо такого дійсного
значення q,
яке б задовольняло (2.28), не існує, то і
нема такого u,
яке задовольняючи нерівності
![]() доставляло б мінімум C(q,
u). Отже, оптимальне
значення u
повинно бути 0 або
доставляло б мінімум C(q,
u). Отже, оптимальне
значення u
повинно бути 0 або
![]() .
Оптимальне значення
.
Оптимальне значення
![]() ,
оскільки нерівність
,
оскільки нерівність
![]() припускає, що постійно мати витрати
із-за втрати замовлень вигідніше, ніж
мати систему, у якій не буває втрат
замовлень. У такому випадку складська
система не потребує управління.
припускає, що постійно мати витрати
із-за втрати замовлень вигідніше, ніж
мати систему, у якій не буває втрат
замовлень. У такому випадку складська
система не потребує управління.
Розглянемо тепер випадок, коли співвідношенню (2.28) задовольняють зразу або одне, або два додатних значення q. Підставляючи q із (2.28) у (2.29), після незначних перетворень одержимо
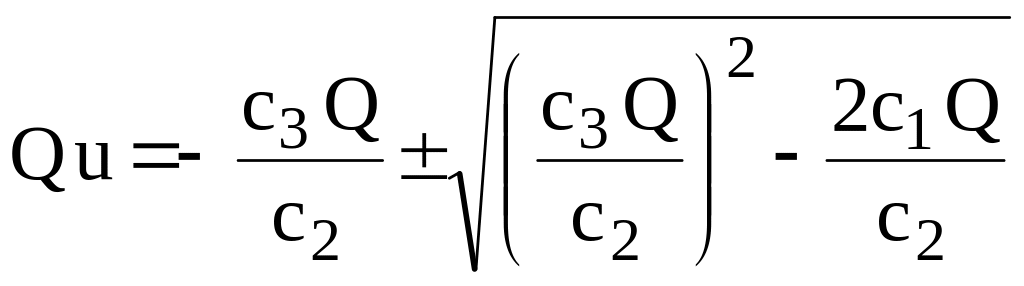 .
(2.32)
.
(2.32)
Однак із (2.31) випливає, що у
(2.32)
![]() для обох знаків перед коренем. У цьому
випадку оптимальне значення
для обох знаків перед коренем. У цьому
випадку оптимальне значення
![]() .
У частинному випадку, коли
будь-яке значення u
буде оптимальним.
.
У частинному випадку, коли
будь-яке значення u
буде оптимальним.
Це означає, що якщо складська система взагалі повинна функціонувати, то допущення дефіциту ніколи не може бути визнано оптимальним.
Коментар: навіть якщо припустити втрату замовлень при , оптимальний розв’язок буде таким самим, як і для моделі без дефіциту.