2.2. Система управління запасами з лінійними витратами

У даній моделі інтенсивність витрачання запасу і витрати на поставку є лінійними функціями відповідно часу t і обсягу поставки q.

Введемо позначення:

– витрати на поставку однієї партії товарів;

– витрати на поставку одиниці товару;

– складова інтенсивності витрачання запасу, незалежна від часу;

– складова інтенсивності витрачання запасу, пропорційна часу.

Згідно введених позначень інтенсивність витрачання запасу і вартість поставки партії товару описуються функціями і .

Розглянемо частинні випадки цієї моделі.

Модель 1:

Позначимо як і раніше через Q обсяг замовлення товару споживачами за час роботи системи T, а через q – розмір партії, яка постачається у кожному із періодів поновлення запасу. Через k позначимо кількість поставок за час T, а через тривалість часу між поставками. Відповідні формули для визначення мають вигляд (2.3).

Функції витрат на поповнення і зберігання запасу відповідно дорівнюють

Загальні очікувані витрати на поповнення і зберігання запасу мають вигляд

(2.13)

Визначаємо похідну від функції C(q)

.

Розв’язуючи рівняння , знаходимо значення , яке дає оптимальне значення розміру поставки.

Приклад 2.2. Визначимо найбільш економічний розмір партії товарів , який мінімізує функцію витрат , а також кількість поставок та інтервал часу між поставками при вхідних даних прикладу 2.1, але при додатковому припущенні, що витрати на постачання партії товару розміру є лінійною функцією від , тобто , де

Розв’язання. З попередньої задачі маємо: загальний обсяг замовлень за період T= 365 днів дорівнює Q = 3650 одиниць, інтенсивність витрачання запасу , витрати зберігання одиниці запасу за добу c₂ = 0,35 грош. од. Коефіцієнти функції витрат на постачання партії товару дорівнюють: грош. од.

Алгоритм реалізації моделі

 задаємо вхідні дані моделі

 записуємо вирази для кількості поставок і інтервалу часу між поставками ;

 визначаємо функції витрат і функцію загальних витрат ;

застосовуючи оператор диференціювання, знаходимо похідну від функції по q;

 розв’язуючи рівняння за допомогою функції Mathcad , визначаємо оптимальний розмір партії постачання ;

 визначаємо оптимальну кількість поставок і інтервал часу між поставками для значення ;

• визначаємо мінімальне значення функції витрат .

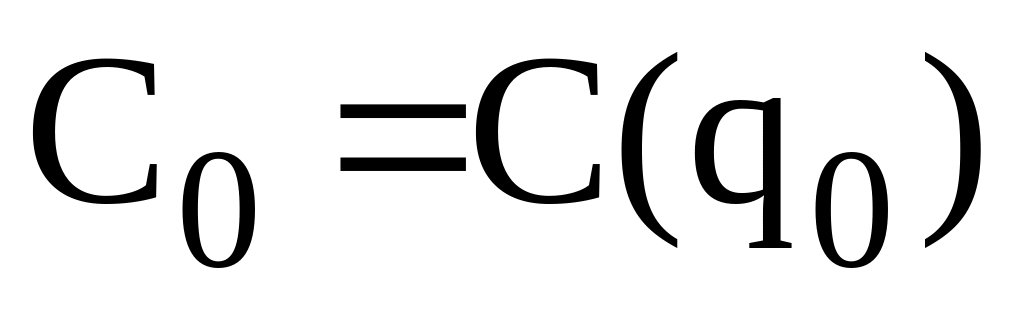Алгоритм у Mathcad

грош. од.

Коментар. Одержали такі результати: розмір найбільш економічної поставки дорівнює одиниць і залишився таким же, як і в попередній моделі. Кількість поставок також не змінилася і дорівнює Інтервал часу між поставками дорівнює доби. Загальні витрати збільшились і дорівнюють 71,9 грош. од. Це сталось у наслідок того, що у витратах на поставку враховується розмір поставки, що збільшує ці витрати. ▲

Модель 2

Обсяг витраченого товару за час t дорівнює b(t), обсяг товару, який зберігається на складі в момент t дорівнює різниці між розміром поставки на початку періоду і обсягом витраченого товару за час t: .

Миттєві витрати в момент часу t дорівнюють а час , за який буде повністю вичерпано запас, є функцією від q і визначається із рівняння

Якщо врахувати, що кількість партій постачання дорівнює , то загальні витрати за період u(q) дорівнюють

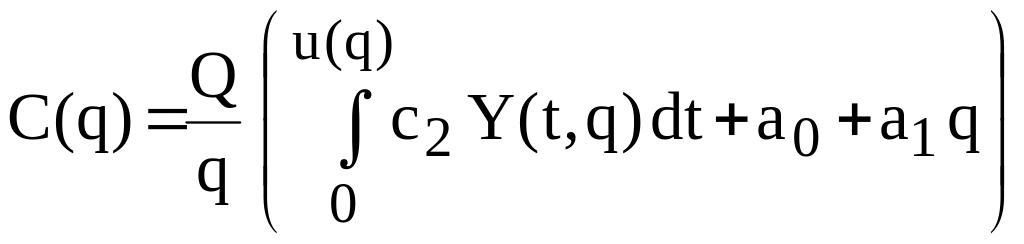. (2.14)

Знаходячи похідну від функції C(q) по q – та розв’язуючи рівняння , одержуємо точку , яка є точкою мінімуму функції C(q). Оптимальне значення функції C(q) знаходимо, підставляючи в неї значення , одержуємо Значення визначає глобальний мінімум, оскільки функція C(q) є строго вгнутою функцією.

Оптимальну кількість поставок і оптимальний інтервал часу між поставками знаходимо за формулами (2.3).

Приклад 2.3. Розглянемо складську систему із наступними параметрами: інтенсивність витрачання запасу і витрати на постачання є лінійними функціями відповідно часу і обсягу партії постачання q: і Для параметрів візьмемо ті ж числові дані, що і в прикладі 2.2: Q=3650, T=365, ,

Визначимо, як і раніше, найбільш економічний розмір партії товарів , який мінімізує функцію витрат C(q), а також обчислимо кількість поставок та інтервал часу між поставками

Розв’язання. Позначаючи довжину періоду, у якому витрачається черговий запас, замість τ через u(q), алгоритм буде мати наступний вигляд.

Алгоритм реалізації моделі

 задаємо початкові значення параметрів моделі:

 записуємо вирази для визначення інтенсивності витрачання запасу b(t), кількості поставок k(q) і інтервалу часу між поставками τ(q);

 визначаємо рівень запасу в момент часу t і момент вичерпання запасу

 визначаємо функції витрат і функцію загальних витрат ;

 знаходимо похідну від функції по q:

 визначаємо оптимальний розмір партії постачання , розв’язуючи за допомогою функції root( ,q) рівняння ;

 визначаємо оптимальну кількість поставок і інтервал часу між поставками за формулами (2.3), підставляючи в них значення ;

 визначаємо мінімальне значення функції витрат грош. од.

Алгоритм у Mathcad

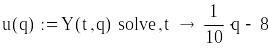
грош. од.

Коментар. Оптимальна стратегія управління запасами у даній моделі передбачає такі значення параметрів системи: розмір найбільш економічної партії поставки дорівнює одиниць, частота замовлень дорівнює разів на рік, відповідний інтервал часу між поставками дорівнює доби. Загальні витрати на постачання і зберігання запасу складають грош. од. ▲