РОЗДІЛ 2. ДЕТЕРМІНОВАНІ МОДЕЛІ

УПРАВЛІННЯ ЗАПАСАМИ

2.1. Система управління запасами без дефіциту

Система управління запасами без дефіциту характеризується постійним попитом у часі, миттєвим поповненням запасу, відсутністю дефіциту і витратами, які не залежать від розміру поставки поповнення запасу. Припущення, що дефіцит не допускається, означає повне задоволення попиту на продукт, що запасається, тобто збіг інтенсивностей попиту r(t) та витрачання b(t).

Модель описується наступними параметрами:

період часу, протягом якого розглядається функціонування системи управління запасами;

загальний обсяг споживання товару протягом часу Т;

інтенсивність витрачання запасу, од. товару / од. часу;

розмір замовлення партії поповнення запасу, од. товару;

час між послідовними замовленнями поповнення запасу (довжина циклу);

витрати на створення або поставку однієї партії товару, які не залежать від її обсягу замовлення;

витрати на зберігання одиниці запасу в од. часу, грош. од.;

витрати на створення або поставку запасу за період T, грош. од.;

витрати на зберігання запасу за період T, грош. од.;

загальні витрати на створення і зберігання запасу за період T, грош. од.

Модель відображає ситуацію управління запасами, яка характеризується наступними припущеннями:

Ø інтенсивність споживання b є відомою і постійною величиною;

Ø час між замовленнями поставок є постійною величиною;

Ø кожне замовлення поставляється у вигляді однієї партії;

Ø витрати на здійснення замовлення не залежать від розміру замовлення q;

Ø відсутність запасу недопустима.

Ця модель найбільш близька до реальних ситуацій, коли попит на товари є сталим або близьким до нього.

Основна задача для системи управління запасами, яка описується даною моделлю, як і для будь-якої іншої, полягає у визначенні того, коли повинно бути

подане замовлення на поповнення і яким повинен бути його розмір.

Оскільки q і τ постійні, а попит і час поставки детерміновані, то звідси випливає, що якщо система функціонує оптимально, то при поданні замовлення кожний раз замовляється одна і та ж кількість товару, а рівень наявного запасу в момент надходження поповнення завжди один і той же.

Інтенсивність витрачання запасу дорівнює відношенню загального обсягу споживання продукту Q і часу T, впродовж якого він витрачається:

(2.1)

Оскільки інтенсивність витрачання запасу дорівнює b, то вся партія буде використана за час τ:

(2.2)

Якщо відлік часу розпочати з моменту постачання першої партії, то рівень запасу в початковий момент дорівнює обсягу цієї партії q, тобто Графік рівня запасу представлено на рис. 2.1.

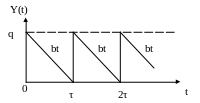
Рис. 2.1. Графік зміни запасу

На часовому інтервалі рівень запасу зменшується по прямій від значення q до 0. Оскільки дефіцит не допускається, то в момент рівень запасу миттєво поповнюється до попереднього значення за рахунок постачання нової партії. Таким чином процес зміни Y(t) повторюється на кожному часовому інтервалі тривалістю . Чим менший розмір замовлення q, тим частіше треба подавати нові замовлення. З іншого боку, із збільшенням розміру замовлень рівень запасу підвищується, але замовлення подаються рідше. Оскільки витрати залежать від частоти подачі замовлень і обсягу запасу, що зберігається, то величина q вибирається із умови забезпечення збалансованості між двома видами витрат – витрат на поставку однієї партії товару і витрат на зберігання запасу за період T. Це лежить в основі побудови відповідної моделі управління запасами.

Задача управління запасами, яка описується даною моделлю, полягає у визначенні такого обсягу партії поповнення запасів q, при якому сумарні витрати на створення і зберігання запасу були б мінімальними.

Оскільки за час Т необхідно запасти Q одиниць продукції, яка доставляється партіями обсягу q, то число таких партій k і інтервал між послідовними моментами поповнення запасу дорівнюють

. (2.3)

Звідси одержуємо вираз для витрат на поповнення запасу

Миттєві витрати на зберігання запасу в момент часу t дорівнюють . Таким чином, за проміжок часу вони складатимуть

Оскільки величина дорівнює середньому запасу за проміжок , то витрати на зберігання всього запасу при лінійному за часом його споживанні дорівнюють витратам на зберігання середнього запасу.

Враховуючи періодичність функції Y(t) (за проміжок часу T буде “зубців”, аналогічних розглянутим на проміжку ), а також формулу (2.3), одержимо витрати на зберігання запасу за проміжок часу T

Із формул для одержуємо сумарні витрати на поповнення і зберігання запасу

. (2.4)

Знайдемо точку мінімуму функції С(q). У точці мінімуму її похідна дорівнює нулю:

.

Із цього співвідношення знаходимо оптимальне значення

, (2.5)

або враховуючи (2.1)

(2.6)

Формули (2.5) і (2.6) називаються формулами найбільш економічного розміру партії поповнення запасів або формулами Уілсона.

Ці формули можуть бути одержані і іншим способом, якщо врахувати, що добуток є величина постійна, не залежна від q. У цьому випадку, як відомо, сума двох величин приймає найменше значення, коли вони рівні, тобто , або

.

Звідси одержуємо формулу (2.5).

Із останнього виразу випливає, що мінімум загальних витрат задачі управління запасами досягається тоді, коли витрати на створення запасу дорівнюють витратам на їх зберігання.

При цьому за формулою (2.4) мінімальні сумарні витрати складають

(2.7)

Звідки, враховуючи (2.1), (2.5), одержимо

або . (2.8)

Якщо відоме, то зручно обчислювати за формулою

Число оптимальних партій за час T з урахуванням (2.1), (2.3) і (2.6)

. (2.9)

Час використання оптимальної партії на основі (2.2) з урахуванням (2.1), (2.5)

або (2.10)

Формула (2.8) дає абсолютний мінімум функції С(q). Дійсно, оскільки

,

то знайдене із рівняння (2.5), доставляє абсолютний мінімум С(q).

Наявний запас коливається між і і в середньому дорівнює . Рівняння (2.6) вказує на той цікавий факт, що середній рівень запасу у системі (а також максимальний рівень і оптимальний рівень q₀) пропорційні кореню квадратному від інтенсивності надходження вимог b. Аналогічно середній рівень запасів обернено пропорційний кореню квадратному від вартості, і тому середній рівень запасів більш дорогих товарів повинен бути при інших рівних умовах нижче, ніж більш дешевих. Таким чином, при виборі стратегії управління запасами слід диференційовано підходити до виробів різної вартості.

Мінімальні річні витрати (при рік) на поставку і утримання запасів при оптимальній стратегії поставок також пропорційні .

Вказаний вираз для буде часто зустрічатись у подальшому і буде позначатись через

На практиці обсяг партії може дещо відрізнятись від оптимального q_0, визначеного за формулами (2.5), (2.6). Виникає питання, як при цьому змінюються сумарні витрати. Для відповіді на це питання порівняємо і С(q), коли q відрізняється від q₀. Для цього обчислимо .

(2.11)

Оскільки вираз не залежить від параметрів системи, то формула (2.11) свідчить про певну сталість значення сумарних витрат C(q) по відношенню до оптимального значення q₀. Це означає, що в околі оптимального значення q₀ крива C(q) має досить плоску форму. Якщо дійсне значення q дуже відрізняється від оптимального, наприклад, у будь якому напрямку на 25 %, то витрати збільшуються при цьому тільки на 2,5 %: Наприклад,

Подібний аналіз показує, наскільки реальні витрати будуть відрізнятись від оптимальних, коли такі параметри як Q або виміряні не достатньо точно.

Припустимо, що поставки здійснюються не миттєво, а протягом певного часу . Тоді замовлення на поповнення запасу в обсязі q одиниць треба подавати в момент, коли наявний запас знизиться до певного рівня . Число називається точкою замовлення.

Нехай m – найбільше ціле число, менше або рівне . Тоді точка замовлення поповнення запасів дорівнює

(2.12)

де = b u – обсяг попиту за час поставки (тобто кількість замовлених одиниць товару з моменту подачі замовлення і до моменту поставки).

Приклад 2.1. Потреба торгівельного підприємства в деякому товарі складає 3650 одиниць на рік. Причому ці товари реалізуються протягом року рівномірно і безперервно. Товари замовляються раз на рік і постачаються партіями однакового обсягу, вказаному у замовленні. Постачання відбувається на початку кожного періоду.

Зберігання одиниці товару на складі коштує 0,35 грош. од. на добу, а постачання однієї партії товару – 5000 грош. од. Затримка реалізації товару через його відсутність недопустима.

Визначимо найбільш економічний розмір партії товарів та інтервал між поставками, які потрібно зазначити в замовленні (передбачається, що постачальник не допускає затримки поставок).

Розв’язання. Сформулюємо задачу у термінах наведеної моделі. За умовою задачі загальний обсяг замовлень за період T= 365 днів дорівнює Q = 3650 одиниць. Витрати на постачання однієї партії складають c₁ = 5000 грош. од., а витрати зберігання одиниці запасу за добу грош. од.

Алгоритм розв’язання задачі.

• задаємо вхідні дані ;

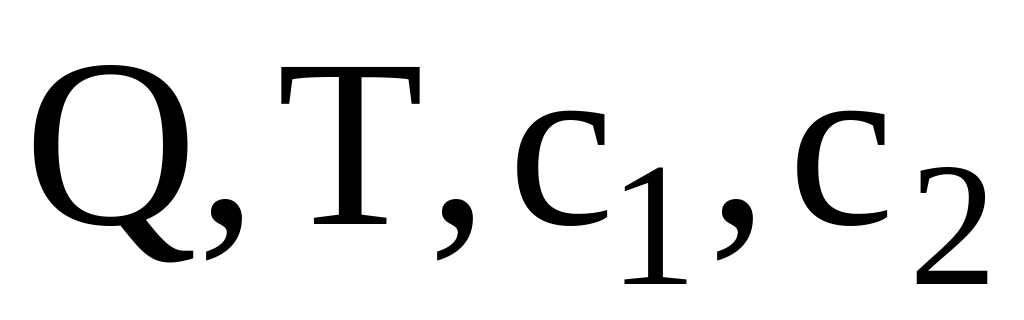• визначаємо інтенсивність витрачання запасу b і записуємо вирази для кількості партій постачання 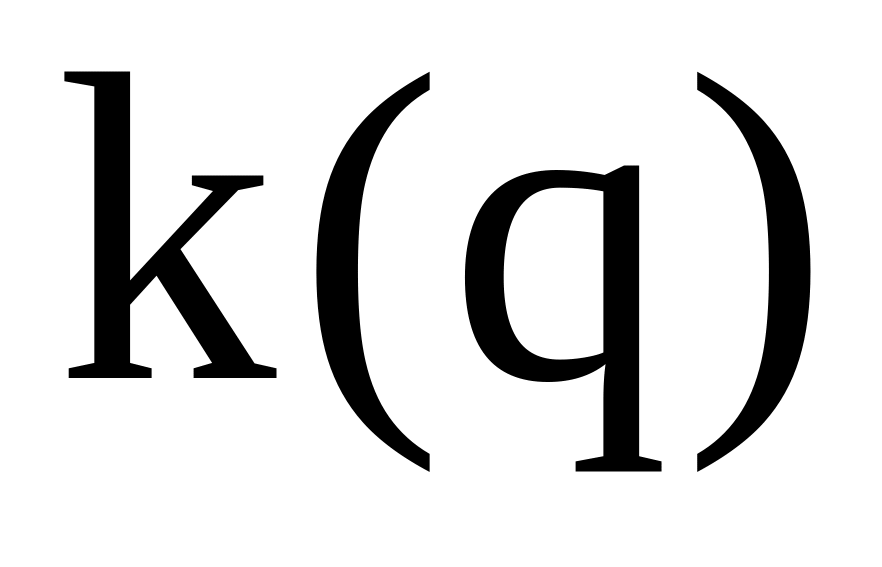і часу між поставками 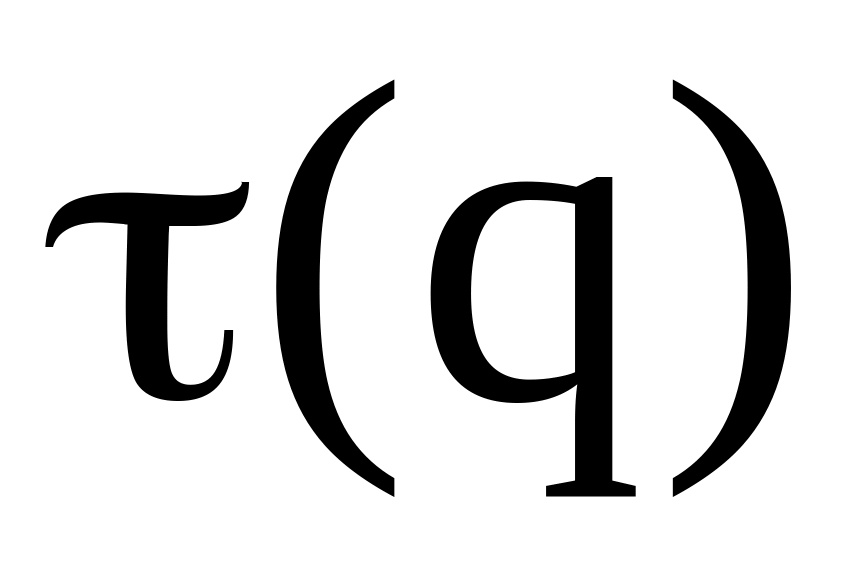як функцій від

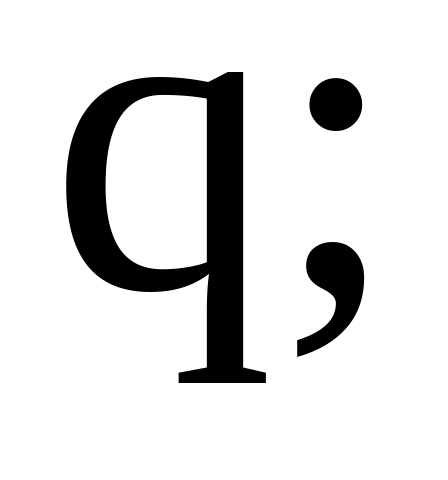
• записуємо вирази для функцій витрат ;

• визначаємо оптимальний розмір партії постачання за формулою Уілсона. Для демонстрації можливостей використання функцій Mathcad для розв’язання задачі знаходимо також , розв’язуючи рівняння 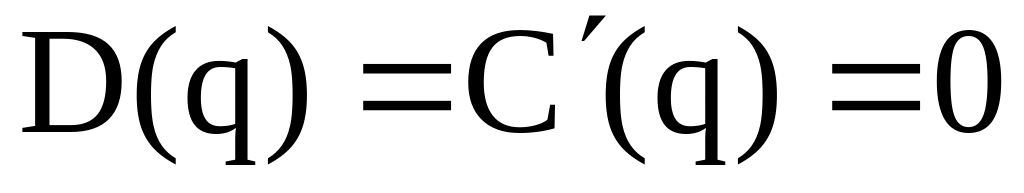за допомогою функції

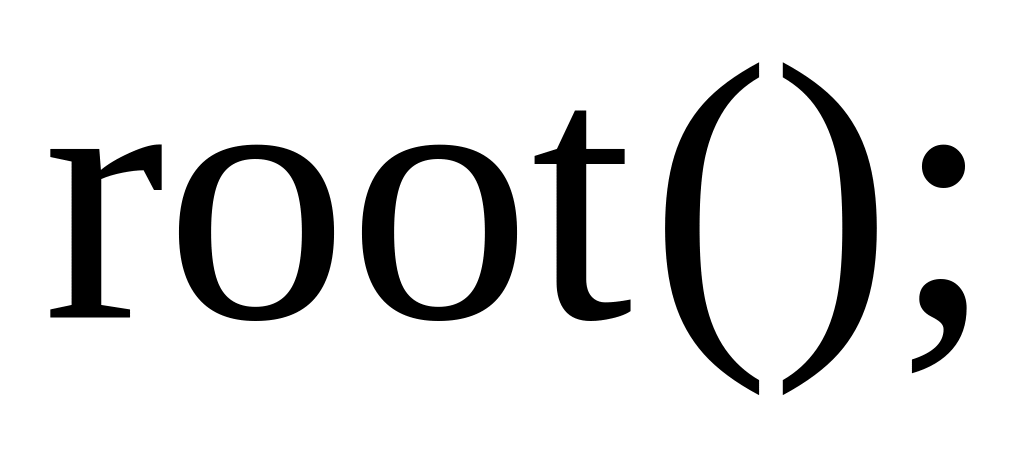
• визначаємо оптимальну кількість поставок і оптимальний інтервал між поставками ;

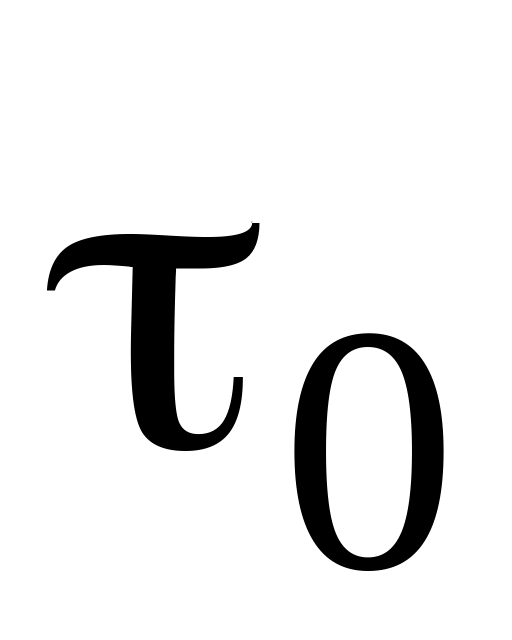• визначаємо мінімальне значення функції витрат

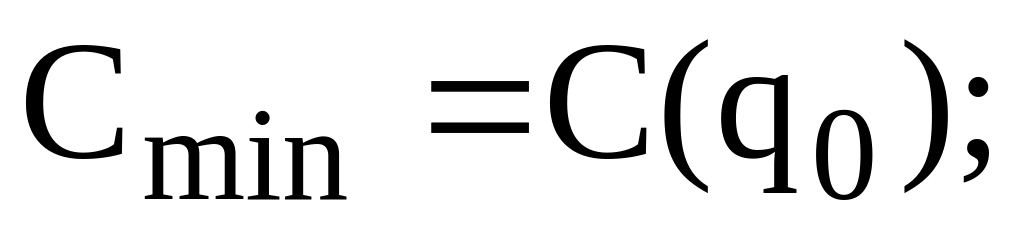
• виводимо графіки функцій

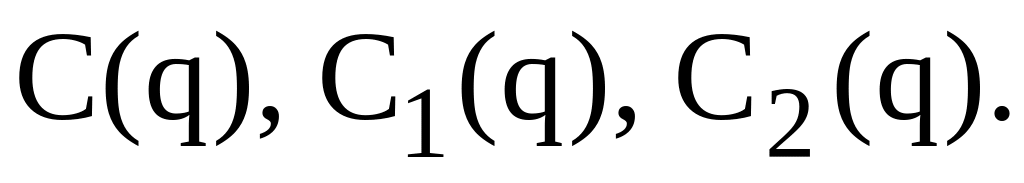
Алгоритм у Mathcad.

Вхідні дані моделі

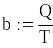
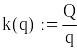
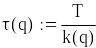
Визначення оптимального обсягу поставки

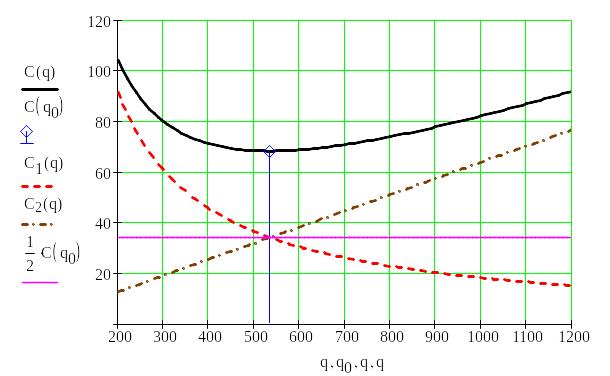
Рис. 2.2. Графіки функцій :

Мінімальне значення функції витрат

грош. од.

Припустимо тепер, що в умовах попередньої моделі замовляються не всі партії зразу, а кожна окремо, причому термін виконання замовлення дорівнює 60 дням. Визначимо точку замовлення, тобто при якому рівні запасу слід замовляти наступну партію.

Оскільки за результатом розв’язання попередньої задачі довжина інтервалу між поставками дорівнює 54 дням, то замовлення в умовах стабільної роботи торгівельного підприємства слід поновити, коли рівень запасу буде достатній для задовільнення потреби на

днів.

Оскільки щоденна потреба (інтенсивність витрати запасу) за формулою (2.1) дорівнює одиницям товару, то замовлення повинні робитись при досягненні рівня запасу до одиниць:

Коментар. Оптимальна стратегія управління запасами може бути сформульована наступним чином: найбільш економічний обсяг партії дорівнює одиниць, кількість поставок у рік , інтервал між поставками дня. Мінімальне значення функції витрат на поставку і зберігання товару при вказаних значеннях і дорівнює = 68,3 грош. од.

Зауважимо, що у Mathcad екстремальне значення будь-якої величини (наприклад, максимальне або мінімальне значення) можна також визначити і графічно. Для того, щоб визначити по графіку значення потрібної величини, клацніть у меню (Формат) у пункті (Графік) по рядку (Слідування), встановіть перехрестя маркера на потрібній точці графіка і виведіть у робочий документ значення , які вказані у вікнах (Величина Х) і (Величина ). ▲