4.3Порядок расчета стойки

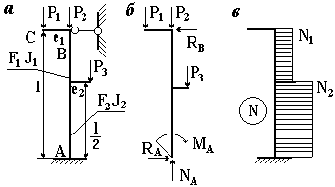
Рассмотрим расчет сварной стойки колонны, жестко закрепленной на фундаменте и имеющей верхнюю связь с другими частями конструкции. Схема нагружения приведена на рисунке 4.8, а. Заданная длина колонны 24 м, длина консоли е₁=0,8 м, консоли е₂=1,2 м, Р₁=300 кН, Р₂=800 кН, Р₃=200 кН. Стойка будет изготавливаться из стали Ст.3 с []=160 МПа, материал фундамента - бетон с []_ф = 5 МПа.

Рисунок 4.8– Расчетная схема колонны

Определим продольные силы в частях стойки: N₁=P₁+P₂ = =1100 кН; N₂=N₁+P₃=1300 кН. Вычислим коэффициент приведения длины . По схеме опирания колонны ₁=0,7; ₂ определим по формуле (4.4), для этого вычислим:

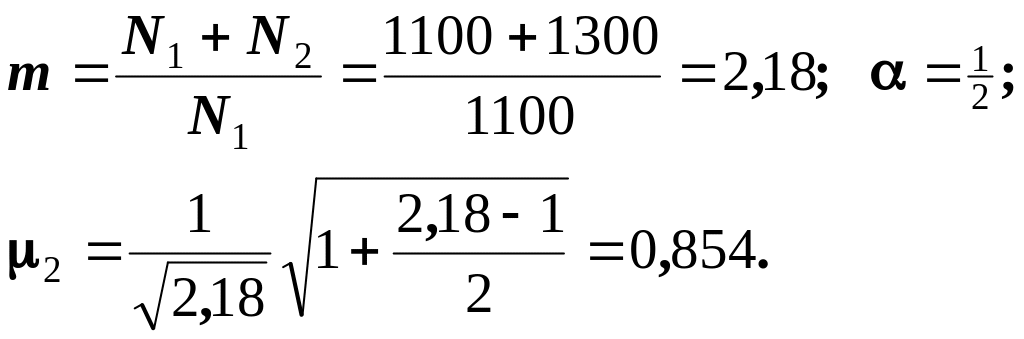
Для вычисления ₃ примем в качестве первого приближения n=J₁/J₂=0,5, тогда по формуле (4.5) получим

м.

По таблице 4.2 и формуле (4.6) вычислим габариты

м; м.

Приняв =0,6, определим по формуле (4.7) требуемые площади сечений

Конструируя сечение колонны согласно варианту задания, предполагаем, что правая часть (по рисунку 4.9) сечения будет сквозной по всей высоте колонны, а швеллер и два уголка будут установлены только внизу. Исходя из размера h_y в качестве элемента № 1 выберем двутавр № 50 со следующими геометрическими параметрами поперечного сечения: F₁=F_дв.=97,8 см²; J_{x_1}=J_x.дв.= =39290 cм⁴; J_{y_1}=J_y.дв.=1040 см⁴; h=50 cм; l=17 см; d=9,5 мм; t=15,2 мм (обозначения по ГОСТу ). Неравнобокие уголки выбираем из сортамента по условию равной местной устойчивости полок уголка с полкой двутавра (т.е. отношения 2t/b_дв.=t/b_уг. ), такому условию соответствует уголок № 12,5/8/1,2: F₂=23,4 см², J_{x_2} = 365 cм⁴.

Рисунок 4.9– Сечение рассчитываемой колонны

Суммарная площадь выбранных элементов 144,6 см², а требуемая площадь верхней части 135,4 м², следовательно, выбранные элементы уже обеспечат прочность стойки на сжатие. Элементы №3, 4, 5 подбираем из конструктивных соображений. В качестве базового элемента № 4 левой части выберем швеллер № 20: F₄=23,4 см², J_{x_4} =J_{x_шв.}=1520 см⁴, J_{y_4}= =J_{y_шв.}=113 см², z_o=2,07 см, h=20 см, b=76 мм, d=5,2 мм, t=9,0 мм. Элемент № 3 - двутавр № 10 – играет роль соединительного элемента правой и левой части, его полки соединяются продольными швами с полками элементов № 1 и № 5 и поэтому местная устойчивость их выше собственной: F₃=12 см²; J_{x_3}=198 cм⁴; J_{y_3}=17,9 cм⁴; b=5,5 см; t=7,2 мм; d=4,5 мм. Неравнобокие уголки (элементы № 5) выбираются так, чтобы длина большей стороны была не меньше h_y=1/2[h_шв.-b_дв.-2(3t_дв.)], 3t_дв. - минимальное расстояние между нахлесточными швами, h_y=1/2[20-5,5+2(3.0,72)]= =9,34 см. Толщина полки уголка должна быть примерно равна толщине полки швеллера. Этим условиям удовлетворяет уголок № 10/6,3/0,8: F₅=12,6 см²; J_{x_5}=J_{x_уг.}=127 cм⁴; J_{y_5}=J_{y_уг.}=39,2 см⁴; x_o=1,5 см; y_o=3,32 см.

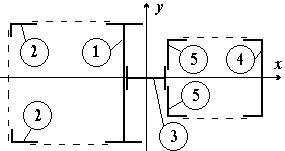
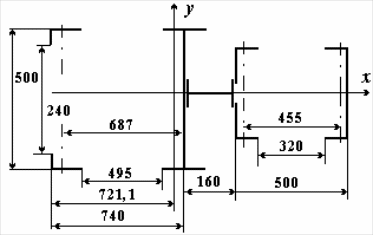
Расстояние между элементами сечения выбираем так, чтобы длина поперечного сечения в направлении оси x была 90 см. Пример расположение элементов поперечного сечения показан на рисунке 4.10. Исходя из принятых размеров вычислим геометрические характеристики. Площадь поперечного сечения F=F₁+2F₂+F₃+F₄+2F₅=205,2 см². Центр тяжести сечения удален от левого края сечения на расстояние x_ц.т.= =(F₁^.55,0+2F₂^.y_o+F₃(55,0+5,0)+F₄(90,0-z_o)+2F₅(65,0+x_o))/F=48,83 см. Моменты инерции J_y=J_{y_1}+F₁^.6,17²+2^.J_{x_2}+2^.F₂^.44,61²+J_{x_3}+F₃^.11,17² +J_{y_4} + +F₄^.39,10²+2^.J_{y_5}+2^.F₅^.17,24²=139835 см⁴; J_x=J_{x_1}+2^.J_{y_2}+2^.F₂^.(25-x_o)²+ +J_{y_3}+J_{x_4}+2^.J_{x_5}+2^.F₅(10-y_o)²=67198 см⁴.

Рисунок 4.10– Размеры поперечного сечения

Определим геометрические характеристики верхней части колонны: F=F₁+2^.F₂+F₃=156,6 см²;

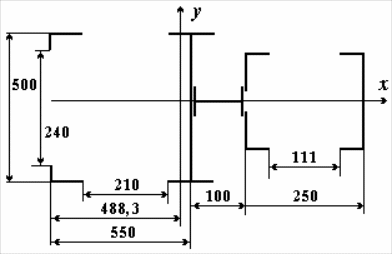
x_ц.т.=(F₁^.55+2^.F₂^.y_o+ +F₃^.60)/F = 40,21 cм;

J_y=J_{y_1}+F₁^.14,79²+2^.J_{x_2}++2^.F₂^.40,21²+J_{x_3}+ +F₃^.19,79²=103645 см⁴.

Для вычисленных значений моментов инерции уточняем коэффициент приведения длины ₃:

Рисунок 4.11–Верхняя часть стойки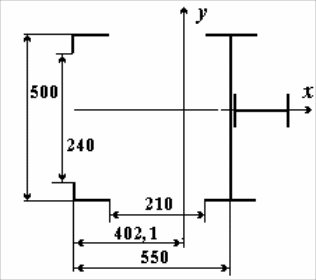

=0,7^.0,854^.1,0868=0,6497;

l_o=15,593 м; h_x=0,866 м; h_y=0,4223 м, что меньше принятых значений.

Для спроектированного сечения вычисляем величины внешних моментов. Силу Р₂ приложим в центре тяжести верхнего сечения. Точка приложения силы Р₁ удалена от левого края колонны на расстояние е₁=1,2 м, тогда плечо силы Р₁ l₁=e₁+x_ц.т. =0,8+0,4021=1,6021 м, а момент М₁=360,63 кН^.м, здесь x_ц.т. - расстояние от левой кромки верхней части сечения стойки до его центра тяжести, рисунок 4.11. Точка приложения силы Р₃ удалена от правого края стойки на расстояние е₂=1,2 м, плечо силы Р₃ l₂=e₂+x_ц.т.=1,2+0,4117=1,6117 м, момент М₃=322,34 кН^.м, здесь x_ц.т. - расстояние от правой кромки сечения нижней части стойки до его центра тяжести.

Рисунок 4.12– Схема сил и моментов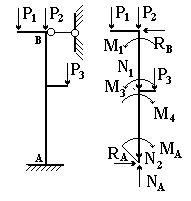

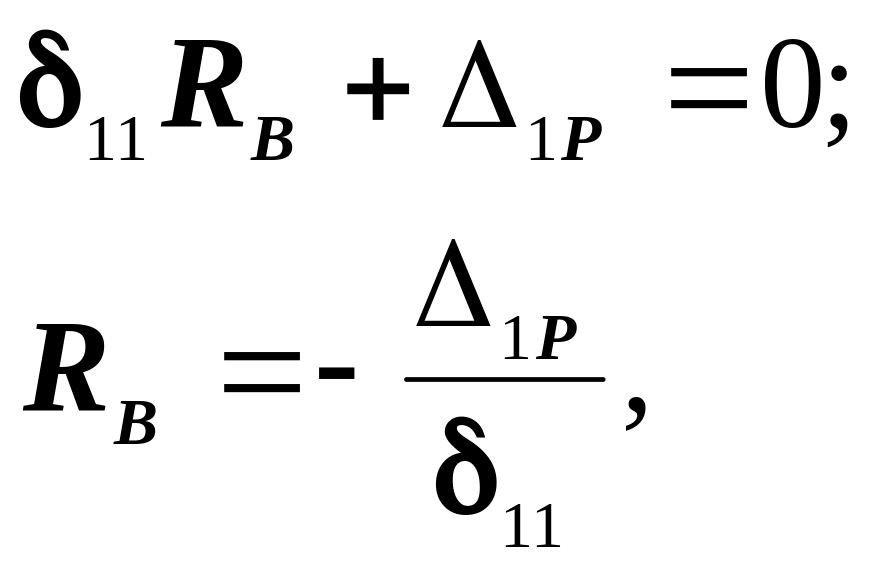Центр тяжести верхней части стойки смещен относительно центра тяжести нижней части на расстояние е₃=0,0862 м, следовательно, сила N₁ создает момент М₄ = N₁^. е₃ = =112,06 кН^.м. В среднем сечении действует момент, равный разности М₃ и М₄ - М_s=M₃- -M₄=150,35 кН^.м. Распределение моментов по длине стойки можно построить, раскрыв статическую неопределимость стойки и определив неизвестные реакции R_A, R_B и M_A. Направление усилий и моментов показано на рисунке 4.12. Неизвестное значение силы R_B можно вычислить методом сил. С этой целью вводим вспомогательную систему без силы R_B, как показано на рисунке 4.13, а, и загружаем ее единичной силой (см. рисунок 4.13, б). Строим эпюры моментов: грузовую М_р (см. рисунок 4.13, в) и единичную М₁ (см. рисунок 4.13, г); М₁=360,63 кН^.м; M₂=150,35 кН^.м. По методу сил

(4.15)

где ₁₁ - перемещения верхнего конца стойки от единичной силы Х=1, определяется способом Верещагина:

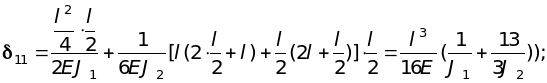
Вычисление перемещений удобно производить с использованием таблиц перемножения эпюр (см. таблицу 3.4 задания 3). Единичные перемещения от внешней нагрузки также вычисляются по правилу Верещагина:

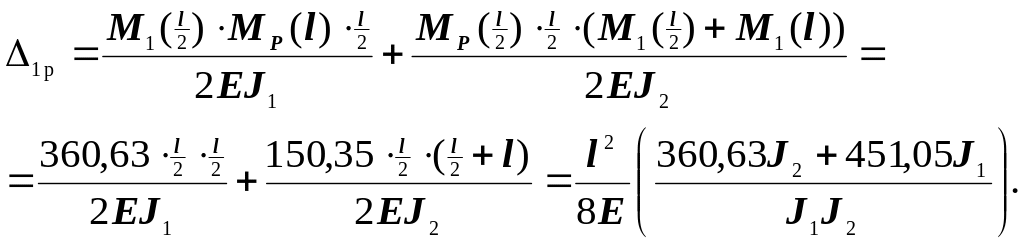
Рисунок 4.13– Вспомогательная расчетная схема

Подставив вычисленные ранее значения J₁ и J₂, получим по (4.15) значение R_В

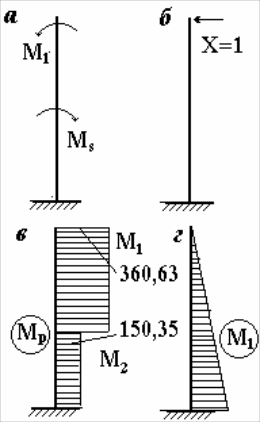
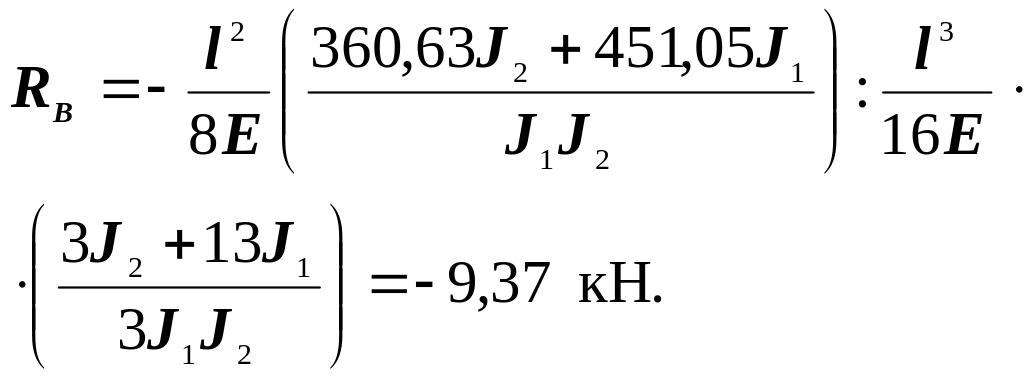
Рисунок 4.14– Эпюра моментов от внешней силы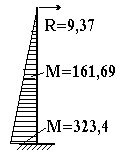

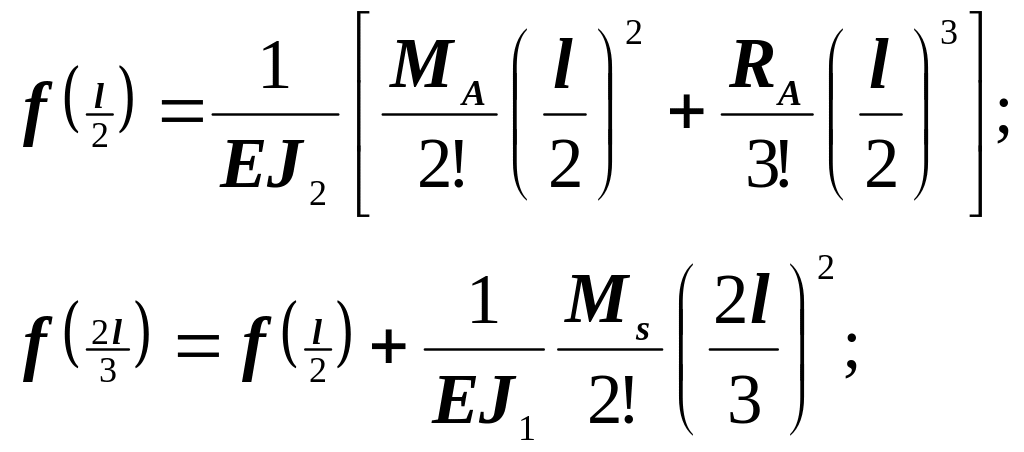
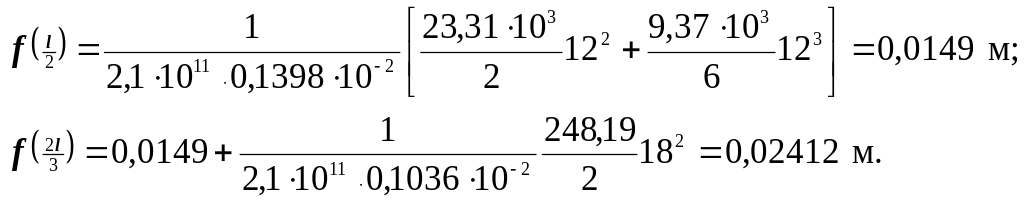
Эпюру моментов от силы R_B строим так, как показано на рисунке 4.14. Объединяя эпюры, приведенные на рисунках 4.14 и 4.13, в, получим исправленную эпюру моментов от внешней нагрузки, приведенную на рисунке 4.15, а. На рисунке 4.15, б приводится эпюра поперечных сил Q. Для уточнения моментов требуется найти прогибы стойки в середине пролета и на уровне 2/3 ее высоты. Для статически неопределимой колонны прогибы удобнее вычислять по методу начальных параметров.

Рисунок 4.15– Эпюры моментов и сил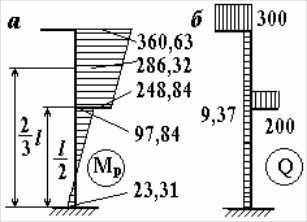

Уточненный момент в сечении стойки на высоте 2/3 ее длины равен:

M_ут=М(2l/3)+N₁^.f(2l/3)=312,85 кН^.м. (4.17)

Уточненный момент в среднем сечении: M_ут=М(l/2)+N₂^.f(l/2)=97,84+19,37 = =117,21 кН^.м. Эксцентриситеты приложения равнодействующих сил определяются в верхнем и нижнем сечениях:

так же, как и ядровые радиусы:

Из сопоставления e_N и _y следует, что верхнюю часть стойки необходимо рассчитывать по варианту Б, а нижнюю – по варианту А. Ядровый момент верхнего сечения определяется по (4.11). Коэффициент продольного изгиба _y принимается по [8, табл. 10.2], как для внецентренно сжатого стержня. Приведенную гибкость и относительный приведенный эксцентриситет вычисляем по (4.12) и (4.13) соответственно. Гибкость стойки вычислим как усредненную гибкость двух ее частей:

, (4.16)

где: ₁, ₂ - гибкости верхней и нижней частей стойки, длинной l₁ и l₂ соответственно, определенные при =2. Для их определения вычислим радиусы инерции:

здесь ₁=93,385, ₂=91,954, =92,6695^.0,6497=60,207. Коэффициент формы  вычислим по (4.14): =1,45-0,003^.60,207=1,269; по (4.13) определим m=3,70, тогда по (4.12) *=1,66. Для полученных значений * и m по [8,табл. 10.2] определим _y=0,283. Ядровый момент по (4.11):

Из сопоставления моментов М_я, М_ут и М₁ наибольшим оказывается М_я, который в дальнейшем будет служить расчетным моментом. Проверяем прочность верхней стойки по (4.8), (4.9):

здесь _x=0,827 определено по [8, табл. 10.1] для _x=76,95; W_y=0,2576^.10^-2 м³;

здесь K=0,6715 вычисляется по (4.10).

Напряжения в плоскости изгибающего момента намного превышают допустимые, следовательно, выбранное сечение не удовлетворяет условию прочности. Анализируя полученные результаты, можно сделать следующие заключения о направлении дальнейшего проектирования.

1. Прочность и устойчивость колонны в плоскости, перпендикулярной изгибающему моменту, обеспечена, следовательно, нецелесообразно изменять размеры прокатных элементов стойки или увеличивать расстояния по оси oy.

2. Изгибающий момент имеет наибольшее значение в верхней части колонны, следовательно, поперечное сечение стойки колонны нецелесообразно делать ступенчатым.

3. Высокие величины напряжений в плоскости изгибающего момента обусловлены как изгибом, так и внецентренным сжатием. В связи с этим следует увеличить расстояние между крайними ветвями стойки и толщины элементов ветвей.

Вычисленные значения напряжений превышают допускаемые примерно в 2 раза, для их уменьшения следует увеличить в 2 раза момент сопротивления, т.е. в раз увеличить расстояния между крайними ветвями. Учитывая значительный вклад в напряжения составляющей от внецентренного сжатия, примем расстояние между ветвями h_x=1,4 м.

Параметры элементов вновь выбранного сечения приведены в таблице 4.3, а размеры– на рисунке 4.16.

Таблица 4.3 – Элементы поперечного сечения

№ элемента	Тип элемента	F, cм2	Jx, см4	Jy, см4	xo, см	yo, см
1	Двутавр № 50	97,8	39290	1040	-	-
2	Уголок № 16/10/1.2	30,0	784	239	2,36	5,32
3	Двутавр № 16	20,2	873	58,6	-	-
4	Швеллер № 30	40,5	5810	327	2,52	-
5	Уголок №12,5/8/1,2	23,4	365	117	2,0	4,22

Пересчитываем геометрические характеристики: i²_y=0,1751, i_y=0,4185, i²_x=0,0321, i_x=0,1792, _y=34,29, _x=80,06, _y=0,935, _x=0,734, W_y=0,6429^.10^-2, m=2,38, =1,347, *=0,94, *_y=0,4534, K=0,7927, e_N=0,4148, _y=0,2501, =0,5978, l_o=14,35 м.

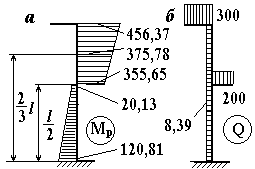
С учетом изменения размеров сечения вновь вычисляем плечо силы Р₁ l₁=e₁+0,7211=1,5211 м и момент М₁=456,33 кН^.м. Плечо силы Р₂ l₂=e₂+0,6789=1,8789 м, М₂=375,78 кН^.м, М₃=80,55 кН^.м. Раскрывая статическую неопределимость по (4.15), определяем R_B=8,39 кН и строим

Рисунок 4.16 – Уточненные размеры сечения

новые эпюры М и Q, приведенные на рисунке 4.17. Вычислим прогиб на расстоянии 2/3 l от основания f(2l/3)= =0,0406 м и по (4.17) уточним момент М_ут=389,21 кН^.м. Из того, что e_N> _y, следует, что расчет сечения стойки нужно выполнять по варианту Б.

Вычисляем по формуле (4.11) М_я=750,51 кН^.м. В качестве расчетного момента принимаем М_я как наибольший из М₁, М_ут и М_я. Проверяем прочность сечения стойки по формулам (4.8), (4.9):

Рисунок 4.17– Исправленные эпюры моментов и поперечных сил

Проверив устойчивость по (4.2)

можно заключить, что превышение _y над [] меньше 5 %, таким образом, прочность и устойчивость спроектированного сечения обеспечена.