
- •Задание 1.Подбор геометрических размеров элементов
- •1.1 Исходные данные
- •1.2 Постановка задачи
- •1.3Пример выбора геометрических параметров сварной фермы
- •1.4 Построение линий влияния
- •1.5Определение максимальных и минимальных усилий
- •1.6Подбор сечения элемента нижнего пояса фермы
- •1.7Подбор сечения элемента верхнего пояса фермы
- •1.8Подбор сечения элемента стоек и раскосов
- •1.9Подбор геометрических параметров сварного соединения раскоса 5-13 с фасонкой
- •1.10 Расчет геометрических размеров фасонки
- •Задание 2.Проектировочный расчет сварной рамы
- •2.1Исходные данные
- •2.2Характеристика метода решения
- •2.3 Дискретизация рассчитываемой конструкции
- •2.4Формирование кэм
- •2.5Внешняя нагрузка
- •2.6Расчет внутренних усилий
- •2.7Проверочный расчет
- •2.8Проверка жесткости конструкции
- •Задание 3. Проектировочный расчет сварной балки
- •3.1Исходные данные
- •3.2Схема решения задания
- •3.3Определение расчетных сечений
- •3.4Определение прогибов балки
- •3.5Определение размеров вертикального листа
- •3.6Определение размеров горизонтальных поясов
- •3.7Определение размеров вертикальных ребер
- •3.8Сварные швы балки
- •3.9Опорные плиты балки
- •3.10Расчет веса балки и веса наплавленного металла
- •Задание 4.Проектировочный расчет сварной колонны
- •4.1Исходные данные
- •4.2Порядок расчета сечения
- •4.3Порядок расчета стойки
- •4.4Расчет соединительных элементов
- •4.5Соединительные продольные швы.
- •4.6Диафрагмы
- •4.7Оголовок колонны.
- •4.8База колонны
- •4.9Расчет веса колонны
- •4.10Расчет веса наплавленного металла
4.2Порядок расчета сечения
Поперечное сечение внецентренно сжатой колонны подбирают из условий прочности:
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
и устойчивости:
![]() (4.3)
(4.3)
Рисунок 4.3– Эпюры сил и моментов
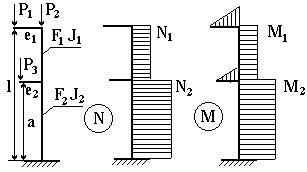
1. Строят эпюры продольных сил и изгибающих моментов, как на рисунке 4.3: M1=P1e1; M2=M1+P3e2; N1=P1+P2; N2=N1+P3. По отношению моментов M1/M2 и продольных сил N1/N2 примерно оценивают отношение моментов инерции и площадей поперечных сечений нижней и верхней ветвей стойки: J1/J2= M1/M2; F1/F2= N1/N2.
2. Определяют приведенную длину стойки lo=l, где - коэффициент приведения длины, определяемый как произведение трех компонент: =123,
здесь 1 - определяется условиями закрепления (см. рисунок 4.2);
2 - определяется положением точки разветвления (см. рисунок 4.3),
![]() (4.4)
(4.4)
3 определяется отношением моментов инерций частей стойки,
![]() (4.5)
(4.5)
3. Первое приближение для определения габаритов поперечного сечения выбирают с учетом некоторых соотношений в стойках. Больший размер сечения hx принимают по таблице 4.2.
Таблица 4.2– Зависимость габаритов стойки от приведенной длины
lo, м |
До 12 |
12 - 16 |
Более 16 |
hx, м |
1/15 lo |
1/18 lo |
1/20 lo |
Меньший размер hy назначают по зависимости
![]() (4.6)
(4.6)
где Kx - числовой коэффициент [1, прил. 4], можно примерно принять Kx=0,4.
4. Задают примерное значение = 0,5 - 0,8 (обычно 0,6) и определяют требуемые площади сечения:
![]() (4.7)
(4.7)
5. Конструируют сечение выбранного типа с габаритами hx и hy и площадями F1 и F2 (размеры прокатных профилей брать из сортамента по ГОСТу).
6. Находят эксцентриситеты приложения
равнодействующей сил, действующих на
стойку:
![]() и ядровый радиус
и ядровый радиус
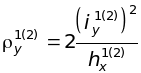 ,
перпендикулярный оси oy. Если
,
перпендикулярный оси oy. Если
![]() ,
то равнодействующая внешних сил проходит
внутри ядра сечения и расчет продолжают
по варианту А, в противном случае –
по варианту Б.
,
то равнодействующая внешних сил проходит
внутри ядра сечения и расчет продолжают
по варианту А, в противном случае –
по варианту Б.
Вариант А. В этом случае основным нагружающим фактором является продольная сила, а изгибающий момент играет второстепенную роль.
Рисунок 4.4– Схемы нагружения стойки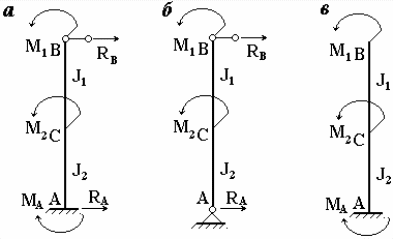
8А. Рассчитывают максимальный прогиб и максимальный уточненный момент. Максимальный прогиб можно определить методом начальных параметров или методом Мора.
Рисунок 4.5– Прогибы колонны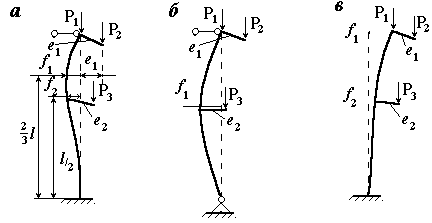
Для определения перемещений по методу Мора строят вспомогательную эпюру от единичной силы, приложенной в расчетной точке. Прогиб определяют по правилу Верещагина, используя таблицы перемножения эпюр (см. таблицу 4.3 задания 3). В случае шарнирно опертой колонны прогиб вычисляется в середине пролета, вспомогательная эпюра приведена на рисунке 4.6.
Применяя метод Мора, получим
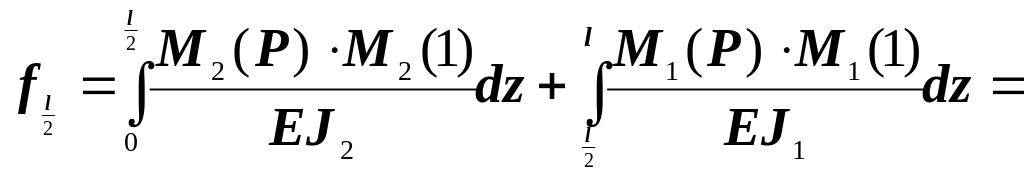
Рисунок 4.6– К расчету шарнирно опертой
колонны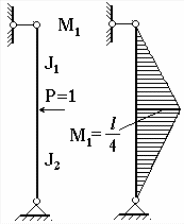
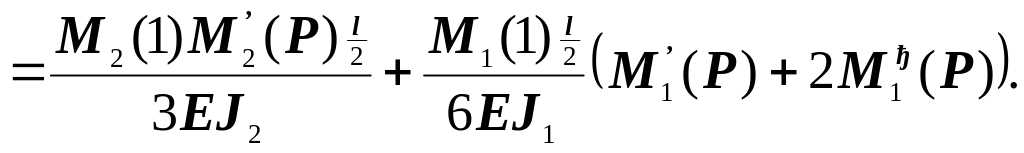
Для жестко опертой колонны определяют перемещения f1 и f2 по рисунку 4.5. Вспомогательные эпюры приведены на рисунке 4.7. Перемещения в начале колонны
Рисунок 4.7– К расчету жестко опертой
колонны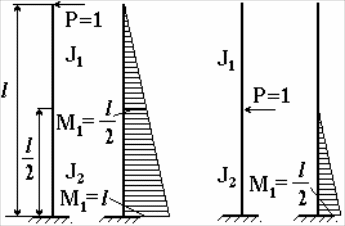
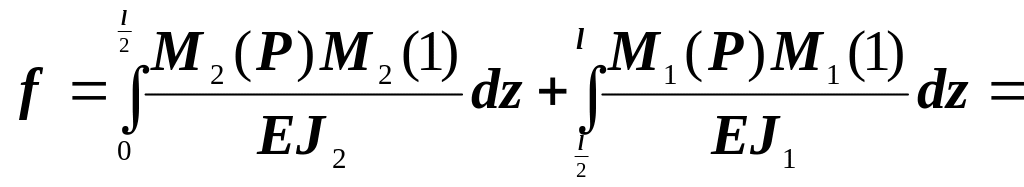
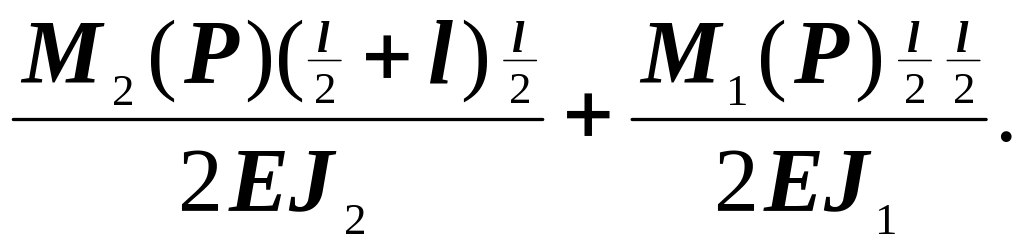
Перемещения в середине пролета
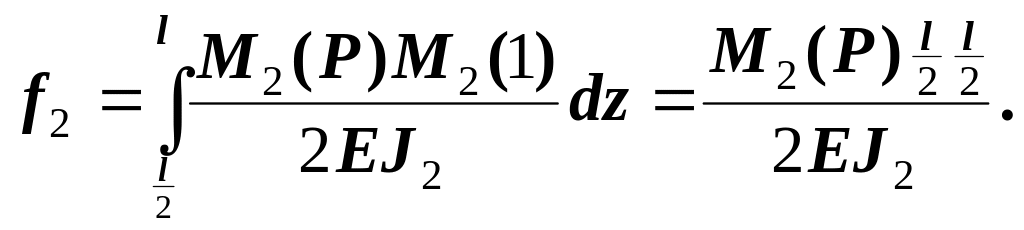
Уточненные моменты определятся как
![]() ,
,
![]() Перемещения для жестко опертой колонны
со связью определяют в двух точках: в
месте наибольшего прогиба f1(2/3l)
и середине колонны f2(l/2).
Перемещения для жестко опертой колонны
со связью определяют в двух точках: в
месте наибольшего прогиба f1(2/3l)
и середине колонны f2(l/2).
9А. Проверяют напряжения от внецентренного сжатия в двух плоскостях: в плоскости нагрузки
![]() (4.8)
(4.8)
и в плоскости, перпендикулярной нагрузке,
![]() (4.9)
(4.9)
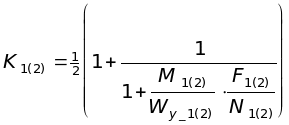 ,
(4.10)
,
(4.10)
а на устойчивость – по формуле (4.2).
10А. Если x и y превышают допускаемые напряжения больше чем на 5 %, то изменяют размеры сечения и повторяют расчет по пп. 7А-9А.
Вариант Б. В этом случае
![]() , т.е. равнодействующая сил проходит за
пределами ядра сечения и главной
нагрузкой является изгибающий момент.
, т.е. равнодействующая сил проходит за
пределами ядра сечения и главной
нагрузкой является изгибающий момент.
7Б. Определяют ядровый момент
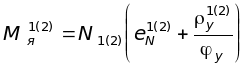 .
(4.11)
.
(4.11)
Коэффициент y определяют по [8, табл. 10.1].
8Б. Определяют требуемый момент сопротивления
![]() .
.
Поскольку начальные габариты hx и hy сечения определены, то из сортамента подбирают элементы поперечного сечения, обеспечивающие требуемые W.
9Б. Конструируют поперечное сечение с габаритами hx и hy , площадями F1 и F2 и моментами сопротивления W1 и W2.
10Б. Вычисляют ix, iy, x, y и учитывают коэффициент продольного изгиба y по [8,табл.10.2]. С этой целью определяют приведенную гибкость
![]() (4.12)
(4.12)
и приведенный относительный эксцентриситет
![]() .
(4.13)
.
(4.13)
В качестве M и N принимают наибольшие значения из Mяд.1(2) и N1(2). Коэффициент формы определяется по типу поперечного сечения, примерно можно считать
=1,45-0,003 . (4.14)
По полученным значениям y и y уточняют Mяд. по (4.11), далее согласно п.7А вычисляют прогибы f и уточненное значение внешнего момента. В качестве расчетного момента принимают наибольшее значение из Мяд. и Мут. и делают проверку прочности и устойчивости по (4.8), (4.9) и (4.2).
11Б. Если x и y превышают допустимые значения больше чем на 5 %, то увеличивают габариты сечения и проектирование повторяют по пп. 8Б - 10Б. Когда сечение подобрано, вычерчивают его в масштабе 1:10 (1:20), рисунок 4.9
