
- •Тіло тиску...……………………………………………………………36
- •7.3. Витікання рідини через малий отвір
- •1. Предмет гідравліки і короткі зведення про її розвиток
- •2. Загальні зведення про рідину
- •2.1. Фізичні властивості рідини
- •2.2. Сили діючі в рідині. Поняття про ідеальні рідини
- •2.3. Робочі рідини для гідравлічних приводів
- •3. Гідростатика
- •3.1. Тиск у крапці спочиваючої рідини
- •3.2. Диференціальні рівняння рівноваги рідини
- •3.3. Основне рівняння гідростатики
- •3.4. Абсолютний, манометричний і вакуумметричний
- •3.5. Сполучені судини
- •3.6. Закон Паскаля
- •3.7. Сила тиску рідини на плоску стінку. Центр тиску
- •3.8. Сила тиску рідини на криволінійну стінку. Тіло тиску
- •3.9. Закон Архімеда
- •4. Основи кінематики рідини
- •4.1. Способи опису руху
- •4.2. Види руху рідини
- •4.3. Потоки, гідравлічні елементи потоку
- •5. Основи гідродинаміки
- •5.1. Диференціальні рівняння руху і балансу енергії для нев'язкої рідини
- •5.2. Рівняння Бернуллі для елементарного струмка нев'язкої рідини
- •5.3. Рівняння Бернуллі для елементарного струмка і потоку грузлої рідини
- •6. Гідравлічні опори. Режими руху рідини
- •6.1. Загальні зведення про втрати напору
- •6.2. Досвіди Рейнольдса. Режими плину рідини
- •6.3. Ламінарний плин рідини в трубах
- •6.4. Ламінарний плин рідини у вузьких щілинах
- •6.5. Турбулентний плин рідини в трубах
- •6.6. Закон гідравлічного опору. Коефіцієнт Дарси
- •6.7. Місцеві опори і поняття про еквівалентну довжину труб
- •7. Витікання рідини через отвори
- •7.1. Витікання рідини через малий отвір у тонкій стінці при постійному напорі
- •7.2. Витікання рідини через малий затоплений отвір при постійному напорі
- •7.3. Витікання рідини через малий отвір при перемінному напорі
- •7.4. Витікання рідини через насадки
- •8. Рух рідини в трубопроводах
- •8.1. Простий трубопровід
- •8.2. Складні трубопроводи
- •1.8.3. Гідравлічний удар у трубопроводах
3.5. Сполучені судини
Н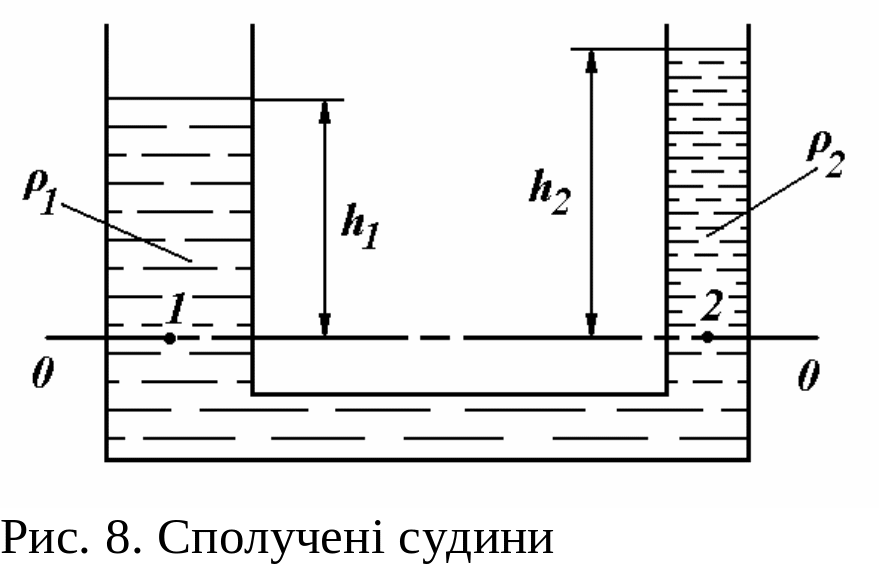 а
рис. 1.8 приведена схема сполучених судин,
заповнених рідинами, що не змішуються,
з різними
а
рис. 1.8 приведена схема сполучених судин,
заповнених рідинами, що не змішуються,
з різними
![]() і
і
![]() щільністю. Проведемо по границі розділу
двох рідин у правому коліні площина
рівного тиску, слід якої на схемі –
горизонтальна лінія
.
Абсолютні тиски в крапках
щільністю. Проведемо по границі розділу
двох рідин у правому коліні площина
рівного тиску, слід якої на схемі –
горизонтальна лінія
.
Абсолютні тиски в крапках
![]() і
і
![]() ,
як і в будь-яких інших крапках рідини,
що лежать на цій площині, будуть однакові:
,
як і в будь-яких інших крапках рідини,
що лежать на цій площині, будуть однакові:
![]() .
Відповідно до основного рівняння
гідростатики (27)
.
Відповідно до основного рівняння
гідростатики (27)
![]() і
і
![]() можуть бути замінені їх значеннями
можуть бути замінені їх значеннями
![]() відкіля
відкіля
![]() (1.31)
(1.31)
тобто висоти стовпів рідин у сполучених судинах назад пропорційні їх щільностям.
Якщо
в сполучені посудини буде налита та
сама рідина, то рівні її в обох колінах
розташуються на однаковій висоті, тому
що
![]() і, отже, з рівняння (31)
і, отже, з рівняння (31)
![]() ,
тобто
,
тобто
![]() .
.
3.6. Закон Паскаля
Помістимо
на вільну поверхню рідини, що знаходиться
в рівновазі в резервуарі (рис. 9, а),
поршень і прикладемо до нього силу
![]() ,
у результаті чого з боку поршня на рідину
виникає тиск
.
Відповідно до основного рівняння
гідростатики (1.27) абсолютні тиски в
довільно обраних крапках рідини
,
,
у результаті чого з боку поршня на рідину
виникає тиск
.
Відповідно до основного рівняння
гідростатики (1.27) абсолютні тиски в
довільно обраних крапках рідини
,
![]() ,
будуть відповідно рівні:
,
будуть відповідно рівні:
![]()
З аналізу отриманих рівнянь видно, що абсолютні тиски в крапках рідини, що знаходяться на різній глибині, будуть різні, однак зовнішній тиск на рідину, укладену в замкнутій судині, передається всім її часткам без зміни. У цьому суть закону Паскаля.
Практично закон Паскаля використовується в ряді гідравлічних машин: гідравлічних пресах і підйомниках, об'ємних насосах і гідродвигунах.
Н а
рис. 9, б
приведена принципова схема гідравлічного
преса. Прикладаючи до меншого поршня
силу
а
рис. 9, б
приведена принципова схема гідравлічного
преса. Прикладаючи до меншого поршня
силу
![]() ,
створюємо в рідині тиск
,
створюємо в рідині тиск
![]() ,
що відповідно до закону Паскаля
передається більшому поршню, викликаючи
силу
,
що відповідно до закону Паскаля
передається більшому поршню, викликаючи
силу
![]() .
Якщо зневажити опорами, то
.
Якщо зневажити опорами, то
![]() (32)
(32)
3.7. Сила тиску рідини на плоску стінку. Центр тиску
В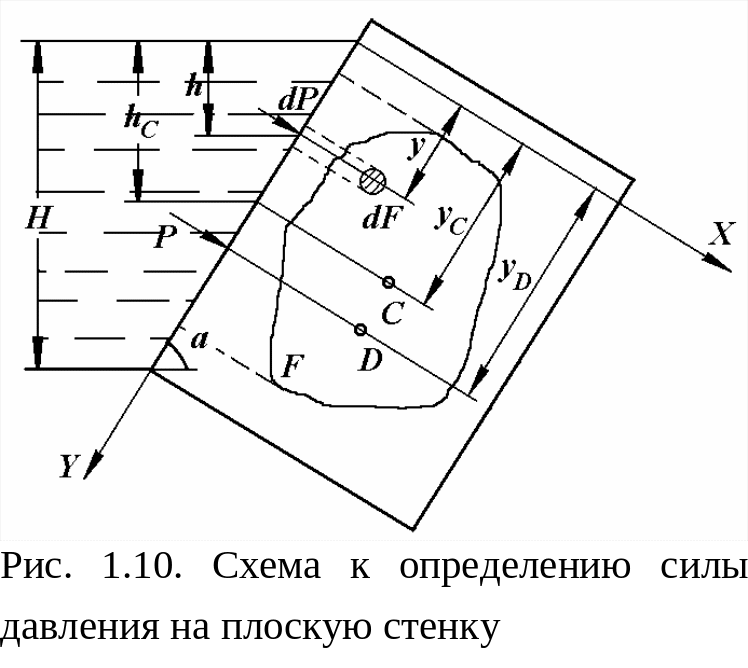 иділимо
на плоскій бічній стінці судини (рис.
10), нахиленої під кутом
,
довільну фігуру площею
і визначимо діючу на неї з боку рідини
силу тиску
иділимо
на плоскій бічній стінці судини (рис.
10), нахиленої під кутом
,
довільну фігуру площею
і визначимо діючу на неї з боку рідини
силу тиску
![]() .
Для наочності сполучимо розглянуту
стінку з площиною креслення (тобто
повернемо її на
.
Для наочності сполучимо розглянуту
стінку з площиною креслення (тобто
повернемо її на
![]() навколо осі
).
навколо осі
).
Тому
що тиск рідини в різних по висоті крапках
площі
різний, то виділимо на цій площі
елементарну площадку, що знаходиться
на відстані
чи від вільної поверхні рідини
![]() від осі
.
Для такої нескінченно малої площі тиск
у всіх її крапках однаковий і дорівнює
від осі
.
Для такої нескінченно малої площі тиск
у всіх її крапках однаковий і дорівнює
![]() ,
отже, сила тиску рідини на елементарну
площадку буде
,
отже, сила тиску рідини на елементарну
площадку буде
![]()
Сила
тиску на всю розглянуту площу
буде
![]()
![]() Вираження
Вираження
![]() являє собою статичний момент розглянутої
площі щодо осі
,
що дорівнює добутку площі
на відстань від її центра ваги до осі
,
тобто
являє собою статичний момент розглянутої
площі щодо осі
,
що дорівнює добутку площі
на відстань від її центра ваги до осі
,
тобто
![]() .
Таким чином,
.
Таким чином,
![]() чи, заміняючи
чи, заміняючи
![]() ,
одержимо
,
одержимо
![]() (33)
(33)
З
(33) видно, що сила тиску рідини на плоску
стінку
дорівнює добутку змоченою рідиною площі
стінки
на гідростатичний тиск у її центрі ваги
![]() .
.
Якщо на вільну поверхню рідини діє тиск, відмінне від атмосферного, силу тиску на стінку можна знайти по формулах:
![]() (34)
(34)
![]() (35)
(35)
де
![]() і
і
![]() – відповідно манометричний тиск і
вакуум на вільній поверхні рідини.
– відповідно манометричний тиск і
вакуум на вільній поверхні рідини.
У ряді випадків, крім значення сили тиску рідини на стінку, необхідно знати координати крапки її додатка – центра тиску.
Припустимо,
що сила тиску
прикладена в крапці
,
що знаходиться від осі
на відстані
![]() .
Відповідно до теореми Вариньона про
момент рівнодіючої (момент рівнодіючої
сили щодо якої-небудь осі дорівнює сумі
моментів складових сил щодо тієї ж осі)
.
Відповідно до теореми Вариньона про
момент рівнодіючої (момент рівнодіючої
сили щодо якої-небудь осі дорівнює сумі
моментів складових сил щодо тієї ж осі)
![]() чи
чи
![]() Замінивши в останнім вираженні
і
Замінивши в останнім вираженні
і
![]() їх значеннях, одержимо
їх значеннях, одержимо
![]() .
Винесемо постійні за знак інтеграла і
скоротимо їх
.
Винесемо постійні за знак інтеграла і
скоротимо їх
![]() .
Вираження
.
Вираження
![]() являє собою момент інерції площі фігури
щодо осі
–
являє собою момент інерції площі фігури
щодо осі
–
![]() ,
що може бути виражений через момент
інерції
,
що може бути виражений через момент
інерції
![]() щодо центральної осі, рівнобічної осі
,
у такий спо-
щодо центральної осі, рівнобічної осі
,
у такий спо-
сіб:
![]() .
Тоді
.
Тоді
![]() ,
відкіля
,
відкіля
![]() (36)
(36)
З
(36) видно, що центр тиску для плоскої
стінки знаходиться завжди нижче її
цента ваги. Горизонтальна координата
центра тиску
![]() знаходиться на осі симетрії площі
фігури.
знаходиться на осі симетрії площі
фігури.
В
окремому випадку, коли
![]() тобто для горизонтального дна судини,
відстань від вільної поверхні до центра
ваги площі
тобто для горизонтального дна судини,
відстань від вільної поверхні до центра
ваги площі
![]() буде дорівнює висоті рідини в судині
буде дорівнює висоті рідини в судині
![]() ,
тому сила тиску рідини на дно судини
,
тому сила тиску рідини на дно судини
![]() .
З цього вираження видно, що різні за
формою судини, що мають однакові площі
дна і заповнені однаковою рідиною на
ту саму висоту, будуть мати однакову
силу тиску на дно незалежно від форми
судини і кількості рідини, що знаходиться
в ньому, (гідравлічний парадокс). Центр
тиску, для дна судини збігається з
центром ваги площі.
.
З цього вираження видно, що різні за
формою судини, що мають однакові площі
дна і заповнені однаковою рідиною на
ту саму висоту, будуть мати однакову
силу тиску на дно незалежно від форми
судини і кількості рідини, що знаходиться
в ньому, (гідравлічний парадокс). Центр
тиску, для дна судини збігається з
центром ваги площі.
