
- •Тіло тиску...……………………………………………………………36
- •7.3. Витікання рідини через малий отвір
- •1. Предмет гідравліки і короткі зведення про її розвиток
- •2. Загальні зведення про рідину
- •2.1. Фізичні властивості рідини
- •2.2. Сили діючі в рідині. Поняття про ідеальні рідини
- •2.3. Робочі рідини для гідравлічних приводів
- •3. Гідростатика
- •3.1. Тиск у крапці спочиваючої рідини
- •3.2. Диференціальні рівняння рівноваги рідини
- •3.3. Основне рівняння гідростатики
- •3.4. Абсолютний, манометричний і вакуумметричний
- •3.5. Сполучені судини
- •3.6. Закон Паскаля
- •3.7. Сила тиску рідини на плоску стінку. Центр тиску
- •3.8. Сила тиску рідини на криволінійну стінку. Тіло тиску
- •3.9. Закон Архімеда
- •4. Основи кінематики рідини
- •4.1. Способи опису руху
- •4.2. Види руху рідини
- •4.3. Потоки, гідравлічні елементи потоку
- •5. Основи гідродинаміки
- •5.1. Диференціальні рівняння руху і балансу енергії для нев'язкої рідини
- •5.2. Рівняння Бернуллі для елементарного струмка нев'язкої рідини
- •5.3. Рівняння Бернуллі для елементарного струмка і потоку грузлої рідини
- •6. Гідравлічні опори. Режими руху рідини
- •6.1. Загальні зведення про втрати напору
- •6.2. Досвіди Рейнольдса. Режими плину рідини
- •6.3. Ламінарний плин рідини в трубах
- •6.4. Ламінарний плин рідини у вузьких щілинах
- •6.5. Турбулентний плин рідини в трубах
- •6.6. Закон гідравлічного опору. Коефіцієнт Дарси
- •6.7. Місцеві опори і поняття про еквівалентну довжину труб
- •7. Витікання рідини через отвори
- •7.1. Витікання рідини через малий отвір у тонкій стінці при постійному напорі
- •7.2. Витікання рідини через малий затоплений отвір при постійному напорі
- •7.3. Витікання рідини через малий отвір при перемінному напорі
- •7.4. Витікання рідини через насадки
- •8. Рух рідини в трубопроводах
- •8.1. Простий трубопровід
- •8.2. Складні трубопроводи
- •1.8.3. Гідравлічний удар у трубопроводах
8. Рух рідини в трубопроводах
Усі трубопроводи можна розділити на прості і складні. Простим називають трубопровід, що складається з труб однакового діаметра і не має по шляху відгалужень, складним – всі інші трубопроводи, що складаються з ряду простих, з'єднаних тим чи іншим способом (наприклад, міський водопровід і ін.).
Розрізняють
короткі і довгі трубопроводи. Короткими
називають трубопроводи, втрати напору
в місцевих опорах яких складають більш
![]() від втрат напору в прямих ділянках
трубопроводу. До них відносяться
всмоктувальні трубопроводи насосних
установок, гідролінії гідроприводів і
ін. Довгими
називаються трубопроводи, у яких втрати
напору по довжині настільки перевищують
місцеві втрати напору, що останніми без
збитку для точності розрахунку можна
зневажити, або прийняти їх орієнтовно
рівними
від втрат напору по довжині.
від втрат напору в прямих ділянках
трубопроводу. До них відносяться
всмоктувальні трубопроводи насосних
установок, гідролінії гідроприводів і
ін. Довгими
називаються трубопроводи, у яких втрати
напору по довжині настільки перевищують
місцеві втрати напору, що останніми без
збитку для точності розрахунку можна
зневажити, або прийняти їх орієнтовно
рівними
від втрат напору по довжині.
У залежності від роду переміщуваної рідини трубопроводи часто називають водопроводи, нафтопроводи, газопроводи і т.д.
8.1. Простий трубопровід
Р озглянемо
простий короткий трубопровід (рис. 30),
що складається з прямолінійних ділянок
і місцевих опорів, і підрахуємо в ньому
втрати напору, для чого скористаємося
принципом додавання втрат:
озглянемо
простий короткий трубопровід (рис. 30),
що складається з прямолінійних ділянок
і місцевих опорів, і підрахуємо в ньому
втрати напору, для чого скористаємося
принципом додавання втрат:
![]()
![]()
![]()
З
отриманого вираження видно, що обчислення
втрат напору цим методом дуже громіздко
і займає багато часу, особливо якщо
трубопровід складається з великого
числа ділянок. Замінимо в цьому вираженні
швидкість витратою
![]() і зробимо приведення подібних членів,
тоді
і зробимо приведення подібних членів,
тоді
![]()
![]() чи
чи
![]() (107)
(107)
Позначимо вираження, що є в дужках, буквою , тоді
![]() (108)
(108)
Величина
називається опором
трубопроводу
і залежить від його довжини, діаметра,
місцевих опорів, а при квадратичному
законі опору і від шорсткості, причому
в останньому випадку для даного
трубопроводу
![]() .
.
8.2. Складні трубопроводи
Послідовне з'єднання трубопроводів.
Розглянемо
складний трубопровід (рис. 31), що
складається з декількох простих
трубопроводів, з'єднаних послідовно й
що мають опори,
![]() ,
,
![]() ,
,
![]() .
.

На
підставі рівняння нерозривності потоку
витрата рідини по кожному з цих ділянок
трубопроводу буде однаковою і дорівнює
,
а втрати напору в них відповідно до
рівняння (108) будуть:
![]() ,
,
![]() ,
,
![]() .
.
Втрати напору в розглянутому трубопроводі відповідно до принципу накладення втрат можуть бути обчислені в такий спосіб:
![]() (109)
(109)
Таким чином, опір складного трубопроводу при послідовному з'єднанні труб збільшується й у загальному випадку складе
![]() (110)
(110)
Паралельне з'єднання трубопроводів.
Розглянемо
складний трубопровід (рис. 32), що
складається з декількох простих
трубопроводів, з'єднаних паралельно.
Нехай опори трубопроводів рівні
,
,
,
а витрати рідини по них
![]() ,
,
![]() ,
,
![]() .
.

Відповідно до рівняння нерозривності потоку загальна витрата рідини по такому трубопроводі буде
![]() (111)
(111)
Втрати напору в кожнім із трубопроводів підраховуються по формулі (108):
![]() (112)
(112)
![]() (113)
(113)
![]() (114)
(114)
Втрати напору в кожнім із простих трубопроводів, а також загальні втрати напору в розглянутому складному трубопроводі будуть рівні різниці повних напорів у перетинах і :
![]() (115)
(115)
З
рівнянь (112) – (115) видно, що
![]() ,
,
![]() ,
,
![]() .
.
Знайдемо з рівнянь (112) – (115) значення витрат у кожнім із простих трубопроводів і підставимо їх у рівняння (1.111):
![]()
Звідси втрати напору в розглянутому трубопроводі будуть
![]() (116)
(116)
Таким чином, опір складного трубопроводу при паралельному з'єднанні зменшується і складає
 (117)
(117)
Разветвленное соединение трубопроводов.
Пусть задано разветвленное соединение трубопроводов (рис. 1.33), состоящее из шести участков труб 1-6 (с известными диаметрами и эквивалентными длинами с учетом местных сопротивлений) и четырех узлов (А, В, С и D). К точке А подводится жидкость с давлением р и расходом q, от точки D жидкость отводится. Требуется определить расходы на всех участках (Q1, Q2, … Q6) и давления в точках В, С и D, то есть девять параметров. Для решения составим девять алгебраических уравнений – шесть выражений потерь давления на участках 1 – 6 и три уравнения расходов в узловых точках:
(1.99)
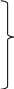

где
![]() -
сопротивление і
– го участка
трубопровода.
-
сопротивление і
– го участка
трубопровода.
