6.7. Місцеві опори і поняття про еквівалентну довжину труб

На відміну від опорів, розподілених по довжині трубопроводу, що виникають на прямих ділянках труб постійного діаметра, при усякому відступі від цих умов (прямолінійності і сталості діаметра) виникають додаткові опори, називані місцевими чи зосередженими. Розширення чи звуження труби (раптове чи поступове), поворот труби (плавний чи різкий під будь-яким кутом), вхід труби в деяку ємність, вихід труби з ємності, вихід рідини з труби в затоплений простір, часткове перекриття труби вентилем (краном) – усе це приклади місцевих опорів.

Втрати напору на місцевому опорі розраховують як частку від динамічного напору по формулі Вейсбаха (79) За рідкісним винятком коефіцієнти місцевих опорів визначаються експериментальним шляхом і приводяться в літературі як довідкові дані. При послідовному розташуванні місцевих опорів у гідромагістралі для находження сумарних втрат окремі коефіцієнти складають. Це можна робити тільки тоді, коли відстань між сусідніми опорами досить велика , для того, щоб потік рідини, вийшовши з попереднього місцевого опору, прийшов у сталий стан перед входом у наступний місцевий опір. У противному випадку принцип суперпозиції (додавання) втрат не застосовується, і обоє ці місцеві опори потрібно розглядати як один (може, не зовсім звичайне) загальний опір.

Для зручності розрахунку спільних втрат, розподілених і місцевих, використовують поняття еквівалентної довжини місцевого опору. Еквівалентною довжиною , називається така довжина прямолінійної (фіктивної, умовної) ділянки трубопроводу, втрати напору в який дорівнюють втратам напору в даному місцевому опорі при однакових витратах рідини. Виходячи з визначення, можна записати: чи відкіля . Тоді спільні втрати в дійсній трубі (довжиною і діаметром ) і місцевому опорі .

Іншими словами, наявність місцевого опору, розташованого поруч із трубою (з параметрами і ), рівносильно (з погляду втрат) подовженню труби на величину до розрахункової величини .

7. Витікання рідини через отвори

В інженерній практиці часто приходиться мати справу з витіканням рідини з отворів різних форм і розмірів, через насадки, водозливи і т.д. Витікання рідини може відбуватися як в атмосферу (незатоплені отвори), так і під рівень (затоплені отвори), при постійному напорі перед чи отвором при перемінному напорі.

7.1. Витікання рідини через малий отвір у тонкій стінці при постійному напорі

Нехай рідина випливає із судини (рис. 26, а) через отвір площею в його бічній стінці. Рівень рідини в судині постійний (за рахунок дуже великих розмірів вільної поверхні чи за рахунок постійного поповнення судини рідиною з зовнішнього джерела) і над отвором має висоту , тобто коли через отвір має місце сталий рух рідини. Завдання полягає у визначенні витрати (швидкості) рідини через отвір. Проведемо два перетини: – у площині вільної поверхні, – у площині отвору, а також площина порівняння – по осі отвору і запишемо для них рівняння Бернуллі

Нехай у загальному випадку тиск навколишнього середовища в резервуарі , а на виході з отвору – , тоді а (в окремому випадку, коли витікання відбувається в атмосферу, у будь-якому перетині струменя тиск буде ). У зв'язку з великим поперечним перерізом резервуара швидкістю в ньому можна зневажити, тому і втрати напору на тертя об стінки резервуара , отже, , де – коефіцієнт місцевого опору (отвору).

Позначимо через – швидкість витікання з отвору, тоді , відкіля

(99)

Позначимо – приведений напір перед отвором; – коефіцієнт швидкості.

Тоді

(100)

Якщо зневажити гідравлічними опорами і нерівномірністю розподілу швидкостей у струмені, тобто прийняти і , що характерно для ідеальної рідини, то й одержимо відому формулу Торрічеллі

(1.101)

Унаслідок того, що , дійсна швидкість витікання буде завжди менше теоретичної . При витіканні води і повітря, коли звичайно має місце турбулентний рух, можна приймати і .

Витрата рідини через отвір може бути обчислений по формулі

При витіканні рідини через малий отвір (рис. 26, б) площею в тонкій стінці внаслідок інерції часток, що рухаються по криволінійних траєкторіях, струм рідини на виході з отвору звужується. На невеликій відстані від отвору утвориться стиснутий перетин, що має мінімальну площу і практично паралельноструміневий рух часток. Позначимо через і назвемо його коефіцієнтом стиску струменя. При так називаному зробленому стиску, коли дно і бічні стінки резервуара відстоять від отвору на відстані не менш трьох – п'ятикратного розміру отвору і не роблять впливу на форму струменя, для отворів круглої і квадратної форми .

Замінимо в рівнянні витрати , а – її значенням з рівняння (100), тоді чи

(102)

де – коефіцієнт витрати отвору.

При зазначених вище значеннях і значення для отворів круглої і квадратної форми складає . Слід зазначити, що зазначені вище значення коефіцієнтів , , мають місце тільки при великих числах Рейнольдса ( і більш), у загальному випадку вони також є функцією .

Формулу (102), маючи в виду те, що пьезометричний напір , можна перетворити до виду

(103)

Формула (103) дуже важлива в розрахунках витрати рідини через отвори, розташовані не тільки в стінках судин, але й у діафрагмах, золотниках, клапанах і інших елементах гідроапаратури.

Застосовуючи той же метод, що був використаний для висновку рівняння (99), і використовуючи рівняння Бернуллі для стисливих рідин (75), можна одержати формулу для визначення швидкості витікання з отвору газу

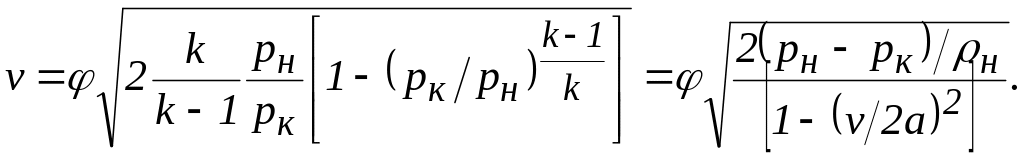(104)

В усіх випадках, коли швидкість витікання газу значно менше швидкості звуку , у спочиваючому газі відношенням можна зневажити і визначати по формулі (1.100).

Масова витрата газу через отвір

(105)