7. Основные элементарные функции. Композиция функций. Элементарные функции

Композиция функций (суперпозиция функций) в математике — это применение одной функции к результату другой.

Композиция функций F и G обычно обозначается . Пусть и две функции. Тогда их композицией называется функция , определённая равенством: .

Элементарными функциями будут называться всевозможные функции, полученные из основных элементарных функция (возможно, многократных) применением операций образования сложных функций, сложения, умножения и деления.

Среди эл-х ф-ий простейшими являются многочлены: P(x) = a₀xⁿ+a_qx^n-1+a₂x^n-2+…+a_n-1x+a_n – суммы целых неотрицательных степеней переменной х с некоторыми коэффициентами, и рациональные функции (дроби) : отношения P(x)/Q(x) двух многочленов.

8. Комплексные числа. Действительная и мнимая части числа. Геометрическое изображение

Комплексным числом называется выражение вида a+bi, где а,b действительные числа, а символ i удовлетворяет условию i²=-i. Множество комплексным чисел обычно называется полем комплексным чисел и обозначается С. Для комплексного числа z=a+bi действительное число а называется действительной частью комплексного числа z и обозначается Rez = a; действительное число b называется мнимой частью комплексного числа z и обозначается Imz=b.

Для понимания различных св-в часто оказывается полезным геометрическое изображение этих чисел точками или векторами на координатной плоскости R² = {(x,y)}, если отождествить комплексное число z=a+bi с точкой с координатами (а,b) или же с радиус-вектором последней точки.

9. Арифметические операции над комплексными числами

Сложение (a + bi) + (c + di) = (a + c) + (b + d)i

Вычитание (a + bi) − (c + di) = (a − c) + (b − d)i

Умножение (a + bi)(c + di) = ac + bci + adi + bdi² = (ac − bd) + (bc + ad)i

Деление

10. Комплексно – сопряженные числа, геометрический смысл операции комплексного сопряжения.

В множестве комплексным чисел С существует ещё одна замечательная операция: комплексному числу z=x+yi можно сопоставить комплексное число , называемое комплексно-сопряжённым к z. Операция комплексного сопряжения имеет простой геометрический смысл, - отражение относительно действительной оси Ох.

11. Произведение комплексно сопряженных чисел и нахождение частного

Произведение комплексного числа z на его комплексно сопряжённое z равно квадрату модуля этого числа . Деление на комплексное число w=c+di≠0 так же возможно: z/w=zw^-/ww^-=1/|w|² *zw^--, и для нахождения частного осталось перемножить два комплексных числа z и w^--.

12. Модуль и аргумент комплексного числа. Геометрический смысл модуля числа и модуля разности 2 чисел

Для z=x+yi неотрицательное число называется модулем числа z, расстояние от z до 0, и, соответственно, |z-w| есть расстояние между комплексными числами z и w, если эти числа рассматривать как точки плоскости.

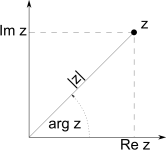
Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.

13. Тригонометрическая форма комплексного числа

Если вещественную x и мнимую y части комплексного числа выразить через модуль и аргумент ( , ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме

, где r=|z|=√a²+b², а tg =b/a

14. Формула Эйлера

В основе ещё одной формы записи комплексного числа лежит замечательная формула Эйлера, связывающая показательную и тригонометрические функции. Формула Эйлера утверждает, что для любого вещественного числа x выполнено следующее равенство: ,где e — основание натурального логарифма, i — мнимая единица.

15. Показательная форма комплексного числа

Используя формулу Эйлера мы можем придать тригонометрической форме записи комплексного числа следующий вид:

Z=|z|e^iф, где для z=a+bi, |z|=√a²+b², а tg =b/a.

16. Модуль и аргумент произведения и частного

Модуль произведения двух комплексных чисел равен произведению из модулей, а аргумент равен сумме аргументов.

Z₁=|Z₁|(cosФ₁+isinФ₁)

Z₂= |Z₂|(cosФ₂+isinФ₂)

Z₁Z₂=|Z₁||Z₂|(cos(Ф₁+ Ф₂) + isin(Ф₁+ Ф₂))

Z₁=|Z₁|e^iф1

Z₂=|Z₂|e^iф2

Док-во: z₁*z₂=|z₁|e^iф1*|Z₂|e^iф2=|Z₁||Z₂|e^i(ф1+ф2)=|Z₁||Z₂|(cos(ф₁+ф₂)+isin(ф₁+ф₂)).

Модуль частного двух чисел равен частному их модулей, а аргумент равен разности аргументов.

Z₁/Z₂=|z₁|e^iф1/|Z₂|e^iф2=|Z₁|/|Z₂|^i(ф1-ф2).