
- •Preface
- •Contents
- •1 Nonideal plasma. Basic concepts
- •1.1 Interparticle interactions. Criteria of nonideality
- •1.1.1 Interparticle interactions
- •1.1.2 Coulomb interaction. Nonideality parameter
- •1.1.4 Compound particles in plasma
- •1.2.2 Metal plasma
- •1.2.3 Plasma of hydrogen and inert gases
- •1.2.4 Plasma with multiply charged ions
- •1.2.5 Dusty plasmas
- •1.2.6 Nonneutral plasmas
- •References
- •2.1 Plasma heating in furnaces
- •2.1.1 Measurement of electrical conductivity and thermoelectromotive force
- •2.1.2 Optical absorption measurements.
- •2.1.3 Density measurements.
- •2.1.4 Sound velocity measurements
- •2.2 Isobaric Joule heating
- •2.2.1 Isobaric heating in a capillary
- •2.2.2 Exploding wire method
- •2.3 High–pressure electric discharges
- •References
- •3.1 The principles of dynamic generation and diagnostics of plasma
- •3.2 Dynamic compression of the cesium plasma
- •3.3 Compression of inert gases by powerful shock waves
- •3.4 Isentropic expansion of shock–compressed metals
- •3.5 Generation of superdense plasma in shock waves
- •References
- •4 Ionization equilibrium and thermodynamic properties of weakly ionized plasmas
- •4.1 Partly ionized plasma
- •4.2 Anomalous properties of a metal plasma
- •4.2.1 Physical properties of metal plasma
- •4.2.2 Lowering of the ionization potential
- •4.2.3 Charged clusters
- •4.2.4 Thermodynamics of multiparticle clusters
- •4.3 Lowering of ionization potential and cluster ions in weakly nonideal plasmas
- •4.3.1 Interaction between charged particles and neutrals
- •4.3.2 Molecular and cluster ions
- •4.3.3 Ionization equilibrium in alkali metal plasma
- •4.4 Droplet model of nonideal plasma of metal vapors. Anomalously high electrical conductivity
- •4.4.1 Droplet model of nonideal plasma
- •4.4.2 Ionization equilibrium
- •4.4.3 Calculation of the plasma composition
- •4.5 Metallization of plasma
- •4.5.3 Phase transition in metals
- •References
- •5.1.1 Monte Carlo method
- •5.1.2 Results of calculation
- •5.1.4 Wigner crystallization
- •5.1.5 Integral equations
- •5.1.6 Polarization of compensating background
- •5.1.7 Charge density waves
- •5.1.8 Sum rules
- •5.1.9 Asymptotic expressions
- •5.1.10 OCP ion mixture
- •5.2 Multicomponent plasma. Results of the perturbation theory
- •5.3 Pseudopotential models. Monte Carlo calculations
- •5.3.1 Choice of pseudopotential
- •5.5 Quasiclassical approximation
- •5.6 Density functional method
- •5.7 Quantum Monte Carlo method
- •5.8 Comparison with experiments
- •5.9 On phase transitions in nonideal plasmas
- •References
- •6.1 Electrical conductivity of ideal partially ionized plasma
- •6.1.1 Electrical conductivity of weakly ionized plasma
- •6.2 Electrical conductivity of weakly nonideal plasma
- •6.3 Electrical conductivity of nonideal weakly ionized plasma
- •6.3.1 The density of electron states
- •6.3.2 Electron mobility and electrical conductivity
- •References
- •7 Electrical conductivity of fully ionized plasma
- •7.1 Kinetic equations and the results of asymptotic theories
- •7.2 Electrical conductivity measurement results
- •References
- •8 The optical properties of dense plasma
- •8.1 Optical properties
- •8.2 Basic radiation processes in rarefied atomic plasma
- •8.5 The principle of spectroscopic stability
- •8.6 Continuous spectra of strongly nonideal plasma
- •References
- •9 Metallization of nonideal plasmas
- •9.1 Multiple shock wave compression of condensed dielectrics
- •9.1.1 Planar geometry
- •9.1.2 Cylindrical geometry
- •9.3 Metallization of dielectrics
- •9.3.1 Hydrogen
- •9.3.2 Inert gases
- •9.3.3 Oxygen
- •9.3.4 Sulfur
- •9.3.5 Fullerene
- •9.3.6 Water
- •9.3.7 Dielectrization of metals
- •9.4 Ionization by pressure
- •References
- •10 Nonneutral plasmas
- •10.1.1 Electrons on a surface of liquid He
- •10.1.2 Penning trap
- •10.1.3 Linear Paul trap
- •10.1.4 Storage ring
- •10.2 Strong coupling and Wigner crystallization
- •10.3 Melting of mesoscopic crystals
- •10.4 Coulomb clusters
- •References
- •11 Dusty plasmas
- •11.1 Introduction
- •11.2 Elementary processes in dusty plasmas
- •11.2.1 Charging of dust particles in plasmas (theory)
- •11.2.2 Electrostatic potential around a dust particle
- •11.2.3 Main forces acting on dust particles in plasmas
- •11.2.4 Interaction between dust particles in plasmas
- •11.2.5 Experimental determination of the interaction potential
- •11.2.6 Formation and growth of dust particles
- •11.3 Strongly coupled dusty plasmas and phase transitions
- •11.3.1 Theoretical approaches
- •11.3.2 Experimental investigation of phase transitions in dusty plasmas
- •11.3.3 Dust clusters in plasmas
- •11.4 Oscillations, waves, and instabilities in dusty plasmas
- •11.4.1 Oscillations of individual particles in a sheath region of gas discharges
- •11.4.2 Linear waves and instabilities in weakly coupled dusty plasmas
- •11.4.3 Waves in strongly coupled dusty plasmas
- •11.4.4 Experimental investigation of wave phenomena in dusty plasmas
- •11.5 New directions in experimental research
- •11.5.1 Investigations of dusty plasmas under microgravity conditions
- •11.5.2 External perturbations
- •11.5.3 Dusty plasma of strongly asymmetric particles
- •11.5.4 Dusty plasma at cryogenic temperatures
- •11.5.5 Possible applications of dusty plasmas
- •11.6 Conclusions
- •References
- •Index

132 |
WEAKLY IONIZED PLASMAS |
the strong polarization interaction with neutral atoms, by the quantity ∆I1 = na 2√πq/2m. Here, q is the total electron–atom scattering cross–section and na is the atomic concentration (see Eq. 1.12). Second, the ion energy in a gas is also reduced by the quantity ∆I2 = 2πnaαe2/ra due to the polarization of the neighboring atoms (see Eq.1.10). The decrease of ionization potential leads to an exponential growth of the electron concentration with density (in this section, we take the absolute value of ∆I). Saha’s equation gives
ne exp[−Im/(2kT )], Im = I − ∆I1 − ∆I2. |
(4.8) |
Let us assume that the electron mobility has a weak dependence on density. Then the electrical conductivity, following variations of ne, grows exponentially with density,
σ |
|
exp[ |
− |
a |
a |
(4.9) |
|
|
(I/2kT ) + (n |
/n )]. |
Here na is the density value starting from which this growth becomes substantial. These formulas yield the following expression for na:
(na)−1 = (2mkT 2/√πq)−1 . (4.10)
The calculated na (4.10) is in good agreement with the experimental value, na 1.7 · 1020 cm−3 (α = 400 a30, ra = 5a0, q = 2 · 10−13 cm2). Smirnov (1970) and Popielawski and Gryko (1977) independently drew the same conclusion.
It should be noted that the mean field approximation used by these authors to calculate ∆I ignores the correlation of atoms in the neighborhood of charged particles. This is valid if the depth of the charge–neutral interaction potential, g, is not too large. However, the value of g/kT is in fact much larger than unity. For estimation, one can use D2+ (the bond energy of Cs+2 or Hg+2 ions) or the polarization well depth αe2/(2ra4). It is easy to see that the correlation is substantial.
4.2.3Charged clusters
Above, we have already discussed the necessity to take into account the correlation of atoms around charged particles. Indeed, in a dense medium the state of charged particles experiences radical changes. Because of attractive forces acting between the charged and neutral particles, charged clusters are formed. The clusters are stabilized due to the presence of charge. The structure of clusters depends strongly on the degree of nonideality. Let us follow the variation of the cluster structure in a vapor upon isobaric heating. On the saturation line (T = Ts) one observes charged droplets. For temperatures somewhat higher than Ts, these are less dense formations which can no longer be regarded as liquid but which are still in dynamic equilibrium with the vapor. At substantially higher temperatures, these are cluster ions containing several atoms and are bound by polarization forces. Finally, in a weakly nonideal plasma the cluster ions dissociate and there remain ordinary molecular ions. The existence of clusters might strongly a ect the properties of matter. For instance, in saturated cesium vapors
ANOMALOUS PROPERTIES OF A METAL PLASMA |
133 |
the thermal emission of electrons from droplets raises the degree of ionization and the electrical conductivity of the plasma by several orders of magnitude. This is responsible for the anomalously high electrical conductivity of high–temperature metallic vapors near the saturation line.
The clusters and similar particles were observed in di erent temperature ranges in numerous gases and liquids, see review by Khrapak and Yakubov (1979, 1981) and Khomkin et al. (1995). Based on the review by Lagar’kov and Yakubov (1980), we shall discuss below the ionization equilibrium in a metal vapor plasma.
We shall start with the simplest case. Let us consider a plasma consisting of electrons, atoms A, ordinary ions A+, and molecular ions A+2 . The electron density is defined by Saha’s equation
n+ne/na λe−3 exp(−βI), |
(4.11) |
||||
and the quasineutrality condition, |
|
|
|
|
|
|
n+ + n2+ = ne. |
|
(4.12) |
||
The concentration of the molecular ion A+ is given by the equation |
|
||||
|
|
2 |
|
|
|
n+ |
+ |
−3 exp( |
− |
βD+). |
(4.13) |
|
na/n2 |
λa |
2 |
|
|
In Eqs. (4.11)–(4.13), n+, ne, na, n+2 stand for the concentration of ordinary ions, electrons, atoms and molecular ions, respectively, λe and λa are the thermal wavelengths for the electron and atom, and D2+ is the bond energy of the atom in the ion A+2 . Let us assume that the degree of ionization is low. Then, by excluding n+2 and n+ from (4.13) with Eqs. (4.11) and (4.12), we obtain
ne2 = nak1 exp(−βI)[1 + nak2 exp(βD2+)], |
(4.14) |
where k1 is the constant of ionization equilibrium in A A++ e and k2 the constant of dissociation equilibrium in A+2 A+ + A. For cesium, k2−1 = 1.45 · 1021T −1/2 cm−3 where T is expressed in eV and D2+ 0.7 eV. It follows from Eq. (4.14) that the inclusion of the molecular ions led to a shift of ionization equilibrium towards increased electron concentration. The higher the molecular ion dissociation energy, the larger is the shift. Under conditions when T = 1400 K and na = 1020 cm3 (near the saturation point for cesium vapors at p = 2 MPa), the inclusion of Cs+2 ions gives an approximately fivefold increase of ne. The electrical conductivity increases accordingly. The important role played by molecular ions in alkali plasmas was confirmed by measurements of the electrical conductivity of sodium vapors near the saturation line by Morrow and Craggs (1973).
The inclusion of Cs+2 ions is not su cient at high pressures and low temperatures, because under these conditions we have nak2 exp(D2+β) 1. This means that n+2 n+. One can naturally expect that a substantial number of Cs+3 ions is present in a plasma. Similarly to Eq. (4.13), for the A+3 A+2 + A equilibrium
134 |
WEAKLY IONIZED PLASMAS |
we have the equation n+3 = n+2 nak3 exp(βD3+). Taking these ions into account, we obtain for n2e instead of Eq. (4.14),
ne2 = nak1 exp(−βI)[1 + nak2 exp(βD2+) |
|
+na2k2k3 exp(βD2+ + βD3+)]. |
(4.15) |
Evidently, as the formation of more and more complex ions (referred to as cluster ions) is taken into account, subsequent terms will appear in the square brackets in Eq. (4.8). Assuming that D3+ = D2+ and k3 = k2/2, the right side of Eq. (4.15) can be regarded as the beginning of a series whose sum is expressed by the exponent. Such summation yields (Likal’ter 1978)
ne2 = nak1 exp[−βI + nak2 exp(βD2+)]. |
(4.16) |
One of the first papers containing the discussion of heavy cluster ions and the summation similar to that performed above, was the paper by Magee and Funabashi (1959).
The procedure of summation in Eq. (4.15) is heuristic. Indeed, even the third term in the series, calculated with due regard for the real values of D3+ and k3, does not correspond to the third term of the exponential series. Nevertheless, Eq. (4.16) represents the major features of the phenomenon. It describes the presence on the isobar of a sharp temperature minimum of free electron concentration and, thereby, of conductivity. Indeed, if σ ne, then
σ σ0 exp[−βI/2 + (nak2/2) exp(βD2+)], |
(4.17) |
where σ0 is some constant. The position of the minimum of electrical conductivity on the isobar approximately corresponds to the value of
Tmin D2+/k ln(nak2D2+/I) .
If p = 2 MPa, then Tmin = 1500 K for cesium, which is in good agreement with experiment. The emergence of the minimum of electrical conductivity is due to the competition between the dissociation of cluster ions and the thermal ionization of atoms.
4.2.4Thermodynamics of multiparticle clusters
As the nonideality becomes stronger, the number of particles in the cluster increases. Therefore, we shall approach the formation of ion clusters from the standpoint of macroscopic thermodynamics. Let an ion be placed in a gas with a mean atomic concentration na and temperature T . Then, if the density of particles attracted by the ion reaches a value corresponding to the loss of thermodynamic stability, the vapor–liquid phase transition occurs in the neighborhood of the ion, in the r < R region. Let us now estimate the value of R. In a steady state, the gradient of the vapor pressure in the neighborhood of the ion must be
ANOMALOUS PROPERTIES OF A METAL PLASMA |
135 |
balanced by the force of attraction of an atom by the ion located at the origin of coordinates,
(M/ρ) grad p = −dV /dr, |
(4.18) |
where V (r) is the potential of the ion–atom interaction and M the atomic mass. Given the equation of state for the vapor, one can integrate Eq. (4.18) to find the density distribution na(r) in the neighborhood of the ion,
p(r) |
|
|
M p |
ρ−1(p, T ) dp = −V (r). |
(4.19) |
In an ideal gas, Eq. (4.19) gives the obvious result,
na(r) = na exp[−βV (r)].
Near the saturation line the interatomic attraction is substantial, p = nakT −an2a, where a is the parameter characterizing the attraction in van der Waals’ equation. In this case, Eq. (4.19) gives, after the integration,
na(r) = na exp{−βV (r) + 2βana[na(r)/na − 1]}. |
(4.20) |
For na = 1020 cm−3 and T = 1400 K at a distance from the ion equal to R = 17a0, the density na(R) exceeds the mean density by a factor of two. The number of particles in a drop of the calculated radius is close to 20. As the number of atoms in a complex increases, the valence electrons will be located on molecular orbitals around the entire complex and will form a band whose width increases as yet another atom is added.
Properties of an ion cluster containing a few dozens of particles are close to metallic. On the other hand, of course, it might still be far from having all the inner properties of a large metal sample (Montano et al. 1986). If equal numbers of positive and negative ion clusters were formed, no anomalous growth of free electron concentration would be observed. In fact, the electron–atom interaction is weaker than the ion–atom interaction (although their polarization asymptotes are identical). This is reflected even by the fact that the bond energy of a positive ion D2+ is substantially higher than that of a negative ion E. For cesium, D2+ 0.7 eV and E = 0.47 eV, and for mercury the bond energy of the ion is D2+ 1 eV while the mercury atom does not bind an electron at all. Therefore, it turns out that the number of positive ion clusters in a plasma is much higher than the number of negative clusters. Consequently, a large number of free electrons is present in the plasma. The electronic transport coe cients are proportional to the free electron concentration and, therefore, they are very sensitive to the concentration ratio between the positive and negative clusters.
Let us now consider how the emergence of ion clusters shifts the ionization equilibrium. We follow a simple model described by Khrapak and Yakubov (1981). This model takes into account the ion–atom interactions and ignores the
136 |
WEAKLY IONIZED PLASMAS |
interatomic and electron–atom interactions. Assume that F0 is the free energy of a mixture of ideal gases of electrons, atoms, and ions. The free energy of the system, F (with due regard for interaction), is lower than F0 by the quantity kT n+g, where g is the number of ions in a cluster. This quantity is close to the excess number of atoms around the ion,
g = na |
dr[exp(−βV ) − 1]. |
|
Thus, |
|
|
F = F0 − kT n+na |
dr[exp(−βV ) − 1]. |
|
By implementing for F a conventional procedure of variation with respect to the concentrations of particles involved in the ionization reactions and taking into account the quasineutrality, we obtain the equation of ionization equilibrium,
n2e = nak1 exp{−βI + na dr[exp(−βV ) − 1]}. (4.21)
Equation (4.21) includes the exponential density dependence of electron concentration, which describes the increase of ne upon compression. Of considerable importance is the presence in the exponent of strong temperature dependence,
∆I = nakT dr[exp(−βV ) − 1]. The potential V (r) can be characterized by two parameters, namely, by the (spherical) volume of the force action between the ion and atom, v0, and the potential well depth, q. At low temperatures, the principal relations are reproduced by a simple formula analogous to Eq. (4.17),
σ = σ0 exp[−βI/2 + (nav0/2) exp(βq)]. |
(4.22) |
At low pressures, the densities na are low and therefore the conductivity grows monotonically with heating. At pressures of the order of p pc the nonideality leads to the emergence of a minimum of conductivity on the isobar. This occurs at temperature
Tmin = q/k[ln(I/qnav0)]. |
(4.23) |
As in the case discussed above, let us assume q = 0.7 eV for cesium. The radius of the ion–atom forces is assumed to be equal to 10a0 (which is close both to the polarization radius (αe2β/2)1/4 and the internuclear distance of the Cs+2 ion). Then, Eq. (4.23) gives Tmin = 1700 K for the 2 MPa isobar, and Tmin = 2500 K for the 15 MPa isobar.
4.2.5“Vapor–liquid” phase transition and metallization
It follows from diagrams showing regions of the existence of nonideal plasma of alkali metals and mercury (see Fig. 1.4) that these regions adjoin the high– temperature part of the two–phase region.
ANOMALOUS PROPERTIES OF A METAL PLASMA |
137 |
The question of how the metallization is related to the liquid–vapor phase transition was already discussed by Zel’dovich and Landau (1944). Two possibilities have been mentioned – the coincidence of the thermodynamic critical point with the metal–dielectric transition, and the loss of metallic properties in the liquid phase region. The latter was apparently revealed in mercury experiments by Kikoin and Senchenkov (1967), and Hensel and Franck (1968). The temperature coe cient of electrical conductivity lost the value characteristic of metal at a density of ρ 9 g cm−3 (Fig. 1.4) exceeding considerably the critical density ρc 5.8 g cm−3 (Kikoin and Senchenkov 1967). In the density range of 4–6 g cm−3, i.e., near and below the critical point, gaseous mercury has typical properties of semiconductors (Kikoin and Senchenkov 1967). Conductivity decreases much below the minimum metal value (although it is still ten orders of magnitude higher than that calculated for an ideal gas) and grows exponentially with temperature at constant density. The value of the dielectric permittivity varies between a few and ten, i.e., is typical of semiconductors. In cesium, the metal–dielectric transition apparently occurs in the critical density region. This is indicated by measurements of electrical conductivity (Alekseev and Vedenov 1970; Renkert et al. 1969) and data on magnetic susceptibility (Franz et al. 1980).
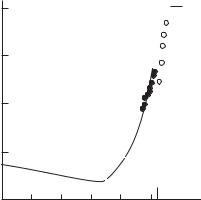
Figure 4.3 demonstrates the electrical conductivity of cesium and mercury at temperatures slightly above the critical. There is a qualitative di erence between the values of electrical conductivity for mercury and cesium. At ρ ρc, the electrical conductivity of mercury (10−1 ohm−1cm−1) is three orders of magnitude smaller than that of cesium (200 ohm−1cm−1). The latter value corresponds to the level of minimum metallic conduction in accordance with Mott’s theory (Mott and Devis 1971) while the former value is too low. This (along with the data on the temperature coe cient of conductivity, thermal e.m.f., etc.) leads to the following conclusion: In mercury, in the neighborhood of the critical point, the phase transition is similar to the transition in nonmetallic media, i.e., liquid mercury at high density exists in the metallic state and at lower density, in the low–conducting state. For cesium (as well as for potassium and rubidium), the “liquid–gas” and “metal–nonmetal” transitions coincide.
The isotherm of electrical conductivity for mercury, shown in Fig. 4.4, gives a clear indication of the behavior of the dielectric–metal transition. The transition range in density is stretched out by an order of magnitude. This indicates that the first stage of metallization is due to the presence of long–range forces showing up even at moderate densities. Such an interaction is the polarization interaction of ions and electrons with atoms. Many years ago, Herzfeld (1927) proposed the criterion of metallization discussed by Frenkel (1955). The ionization potential (the bond energy of electron and atom) in a dense medium, Im = I/ε, decreases according to the microscopic theory because of the increase of dielectric permeability ε. In accordance with the Clausius-Mossotti equation,
ε = 1 + 4πnaα(1 − 4παna/3)−1. |
(4.24) |
138 |
WEAKLY IONIZED PLASMAS |
|
|
σ, ohm-1 cm-1 |
|
|
104 |
1 |
|
1 |
|
|
10−4 |
|
|
10−8 |
|
|
2 |
|
|
10−12 |
1021 na, cm−3 |
|
1017 1018 1019 1020 |
|
Fig. 4.4. |
Isotherm of electrical conductivity |
for mercury, T = 1973 K (Khrapak and |
Yakubov 1981). Measurement results: ◦ — (Hensel and Franck 1968); • — (Kikoin and Senchenkov 1967); 1 — level of electrical conductivity for metal; 2 — electrical conductivity for ideal plasma.
If the density increases to approach the value of 3/(4πα) (where α is the polarizability in the gaseous state) the dielectric permeability increases indefinitely, which is typical for metals. Case na > 3/(4πα) corresponds to spontaneous ionization, i.e., the transition of electrons to the free or, rather, collectivized state. In other words, if na 3/(4πα), the material is a metal. The value of 3/(4πα) equals approximately 4 · 1021 cm−3 for cesium and 4 · 1022 cm−3 for mercury. These values coincide to within the order of magnitude with the observed transition values.
High–temperature vapors of some metals in the vicinity of the saturation line are nonideal because of the charge–neutral and charge-charge interactions. However, the results of measurements of p–ρ–T -dependencies for cesium and mercury, given in Figs. 2.20 and 2.21, failed to point explicitly to any peculiarity in the equation of state that would be due to the plasma e ects. Nevertheless, it was suggested by Khrapak and Yakubov (1970), and Starostin (1971) that the vapor condensation in the high–temperature region is largely due to plasma e ects. The critical parameters of cesium shown in Table 4.1 were estimated by using the methods of the nonideality description developed by Kraeft et al. (1985).
Apparently, these assumptions about the nature of phase transition in metals are valid. Then one can hardly expect that, at higher temperatures, plasma interactions will once again cause the phase separation. The interesting possibility of a new “plasma” phase transition was discussed by Norman and Starostin (1970) (see Chapter 5 below).
