
Основы проектирования машин / ГЛАВА 3
.4.pdf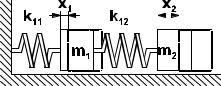
ГЛАВА 3.4. ТЕОРИЯ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ
Знание основ теории механических колебаний необходимо инженерам, работающим в различных областях машино-, авиа- и судостроения, промышленного и транспортного строительства и т. д. Колебательные процессы, протекающие в разного рода технических устройствах, оказывают огромное, часто даже решающее, влияние на условия эксплуатации конструкций, их прочность и долговечность, а также здоровье работающих с подобной техникой людей. Причем надо отметить, что механические колебания могут как причинить большой вред, так и принести значительную пользу. Несмотря на специфику связанных с колебаниями практических задач, решаемых каждой из названных областей, все они объединены общими принципами и методами, составляющими суть теории колебаний. Дело в том, что совершенно разные по физической природе колебательные процессы описываются одинаковыми по форме уравнениями. Специфика каждой конкретной задачи фиксируется входящими в эти уравнения константами, зависящими от физической природы изучаемого явления.
В настоящей главе рассматривается теория малых линейных механических колебаний, имеющая наибольшее применение в технике. Вначале исследуются свободные колебания, т. е. колебания автономных систем, происходящие под действием восстанавливающих и, в общем случае, диссипативных сил около состояния равновесия (напомним, что восстанавливающими называются силы, возникающие при отклонении системы от положения равновесия и направленные таким образом, чтобы вернуть систему в это положение; в роли восстанавливающих выступают, как правило, появляющиеся при деформировании упругие силы, а также сила тяжести и сила Архимеда). Затем - вынужденные колебания, вызываемые и поддерживаемые так называемыми вынуждающими силами, зависящими от времени и не зависящими от характера движения системы.
Свободные колебания линейных систем с несколькими степенями свободы.
Дифференциальное уравнение колебательного движения. Свободные колебания в чистом виде встречаются в механических системах не слишком часто. Тем не менее их изучение очень важно, так как именно характеристики свободных колебаний, такие как собственные частоты и собственные формы, полностью определяют индивидуальные физические и динамические свойства механической системы и имеют важнейшее значение при анализе вынужденных колебаний.
Существует несколько способов составления дифференциальных уравнений колебательного движения. Наиболее общим из них является метод уравнений Лягранжа [4, 29]. Однако, как это часто бывает с общими методами, во многих задачах о колебаниях его применение неоправданно громоздко, и удобнее пользоваться более непосредственными приемами. Рассмотрим один из таких способов, называемый прямым методом записи уравнения движения (существует также и обратный метод, но здесь он рассматриваться не будет). Согласно этому методу, составляющие систему тела трактуются как свободные материальные точки (или твердые тела), находящиеся под действием восстанавливающих сил, выражаемых через обобщенные координаты. Для этих материальных точек (твердых тел) и записываются дифференциальные уравнения движения.
Основное дифференциальное уравнение свободных колебаний консервативных упругих линейных систем с несколькими степенями свободы, составленное прямым способом, рассмотрим на примере системы, состоящей из
двух грузов с массами m1 и m2 , соединенных двумя упругими пружинами с жесткостями k11 и k12 (рис. 3.4.1a). Эта система обладает двумя степенями свободы. При движении грузов происходит деформирование упругих
элементов системы. Если грузы перемещаются на расстояния x1 и x2 от положения равновесия, в котором пружины не деформированы, то удлинения пружин в процессе движения равны ∆l1 = x1 , ∆l2 = x2 − x1 .
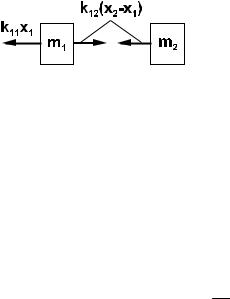
Деформации пружин вызваны возникновением реактивных сил упругости R1 и R2 , определяемых удлинениями
∆l1 и ∆l2 (рис. 3.4.1b):
R1 = k11 x1 ; R2 = k12 (x2 − x1 ). |
(3.4.1) |
||
|
|
|
|
|
|
|
|
a)
b)
Рис. 3.4.1
Дифференциальные уравнения движения грузов в соответствии со вторым законом Ньютона имеют вид
m x = −R + R ; |
|
||||
|
&& |
|
|
|
|
1 |
1 |
|
1 |
2 |
|
|
&& |
d 2 x2 |
= −R2 |
|
|
|
|
2 |
. |
||
m2 x2 |
dt |
||||
|
|
|
|
|
|
x& = dx ; &x&=
Здесь, как обычно, точкой обозначается производная по времени, т. е. dt подстановки в (3.4.2) выражения для реакций со стороны упругих элементов (3.4.1) получаем
m1 x1 = −k11 x1 + k12 (x2 − x1 ); |
||
&& |
|
|
&& |
= −k12 (x2 − x1 ). |
|
m2 x2 |
|
|
|
(3.4.2) |
d 2 x |
|
dt 2 |
и т. д. После |
(3.4.3)
Как видно из формулы (3.4.3), на осадку пружины влияет перемещение соседнего участка. Если перейти к локальной системе координат, то в общем виде деформационное состояние системы с s степенями свободы
можно характеризовать обобщенной координатой |
q j |
, |
j =1,2,......, s |
- номер координаты. В качестве |
|
|
обобщенных координат могут выступать, например, линейные перемещения при поступательном движении или угловые перемещения при вращательном. Для статической упругой линейной системы общего вида справедливо
следующее фундаментальное соотношение, связывающее обобщенные координаты |
q j |
(статические |
|
|||||||||||
|
|
|
||||||||||||
перемещения) с обобщенными силами Fk : |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
q j = ∑s |
δjk Fk |
j =1,2,......, s , |
|
||||
|
|
|
|
|
|
|
k =1 |
, |
(3.4.4) |
|||||
где |
δjk |
- статический коэффициент влияния для перемещений, равный значению |
j |
-ой обобщенной |
|
|||||||||
координаты, соответствующему действию статически приложенной k -ой обобщенной единичной силы. |
|
|||||||||||||
Коэффициент |
δjk |
определяет перемещение или конфигурацию равновесного положения системы, когда к ней |
||||||||||||
|
||||||||||||||
приложена только одна единичная сила |
Fk |
=1 |
. Можно сказать и так: |
j |
- это номер текущей массы |
|
||||||||
|
|
|
|
|||||||||||
колебательной системы, а k - номер соседней массы, влияющей на деформационное состояние текущей. Коэффициенты влияния удовлетворяют условию симметрии,
δ jk = δ jk ,
выражающему принцип взаимности перемещений.
Введя в рассмотрение матрицу - столбец (вектор) обобщенных координат qr , матрицу - столбец
обобщенных сил Fr |
и симметричную матрицу коэффициентов влияния для перемещений [δ], |
|
|
|
|
|
||||||||||||||||
|
|
q1 |
|
|
F1 |
|
|
δ11 |
δ12 |
|
....... |
δ1s |
|
|
|
|||||||
|
r |
|
|
|
r |
|
|
|
|
δ |
|
δ |
|
|
....... |
δ |
|
|
|
|
||
|
q |
|
|
F |
|
|
|
|
|
|
|
|
||||||||||
|
q = |
|
2 |
|
F |
= |
2 |
|
[δ] = |
|
21 |
|
22 |
|
|
|
|
2 s |
|
|
|
|
|
|
M |
|
|
|
M |
|
|
..... ....... ........ |
....... |
|
|
||||||||||
|
|
q |
s |
|
|
F |
|
|
|
δ |
s1 |
δ |
s2 |
|
....... |
δ |
ss |
|
|
|
||
|
|
|
|
; |
|
s |
|
; |
|
|
|
|
|
|
|
|
, |
(3.4.5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
перепишем (3.4.4) в матричной форме, а именно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
qr = [δ]Fr |
|
|
|
|
|
|
|
|
|
(3.4.6) |
||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
Разрешим уравнение (3.4.6) относительно вектора Fr . Для этого умножим обе его части слева на |
|
|||||||||||||||||||||
симметричную матрицу [c]= [δ]−1 |
, обратную к |
[δ] |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
c |
c |
|
....... |
|
c |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
11 |
12 |
|
|
|
|
1s |
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
c21 |
c22 ....... |
|
c2s |
|
|
|
|
|
|
|
||||
|
|
|
|
[c]= [δ] |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
..... ....... ........ ....... |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
cs2 ....... |
|
css |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
cs1 |
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получим |
|
|
|
|
|
|
|
|
|
Fr = [c]qr |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
(3.4.7) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Матрица [c] называется матрицей единичных реакций или матрицей жесткости. Физический смысл ее
элементов c jk , называемых статическими коэффициентами жесткости, следующий. Предположим, что на все точки рассматриваемой системы наложены некоторые дополнительные связи, обращающие в нуль все
обобщенные перемещения, кроме k -го, причем равного единице, qk =1. Тогда c jk = Fj , т. е. элемент c jk
представляет собой реакцию j -ой дополнительной силы, соответствующую k -му единичному перемещению.
Коэффициенты жесткости, так же как и коэффициенты влияния, симметричны, c jk = ckj , что является следствием принципа взаимности сил.
Матрица - столбец обобщенных сил Fr , в свою очередь, в соответствии со вторым законом Ньютона имеет вид
Fr = [a]q&r&, |
(3.4.8) |
где [a] - симметричная матрица инерционных коэффициентов,
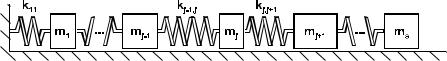
|
a11 |
a12 |
....... |
a1s |
|
|
|
|
a22 |
....... |
a2 s |
|
|
[a]= |
a21 |
|
|
|||
|
|
|
|
|
|
|
|
..... ....... ........ ....... |
|
||||
|
|
as2 |
....... |
ass |
|
|
|
as1 |
|
. |
|||
|
|
|
|
|
|
|
Важно отметить, что при составлении системы уравнений по прямому способу aij
матрица инерционных коэффициентов становится диагональной.
(3.4.9)
= 0 при i ≠ j , т. е.
Соотношения (3.4.7) и (3.4.8) позволяют записать дифференциальное уравнение движения статической
упругой линейной системы общего вида в форме |
|
|
|
|
||
|
|
[a]q&r&+[c]qr = 0 , |
|
(3.4.10) |
||
или |
|
|
|
|
|
|
|
s |
(a jk qk + c jk qk )= 0 |
|
|
|
|
|
∑ |
|
|
|
||
|
|
&& |
|
j =1,2,K, s . |
|
|
|
k =1 |
|
, |
|
(3.4.11) |
|
Для прямого способа вместо (3.4.11) вследствие диагональности матрицы [a] имеем |
|
|
||||
|
|
s |
|
|
|
|
|
|
a j q j + ∑c jk qk = 0 |
|
|
|
|
|
|
&& |
|
j =1,2,K, s . |
|
|
|
|
k =1 |
, |
|
(3.4.12) |
|
В любой из форм уравнения (3.4.10) представляют собой систему дифференциальных уравнений |
||||||
движения, которая в развернутом виде записывается как |
+L+ a1s qs + c1s qs = 0; |
|
|
|||
a11q1 |
+ c11q1 |
+ a12 q2 + c12 q2 |
|
|
||
&& |
|
&& |
|
&& |
|
|
a21q1 |
+ c21q1 + a22 q2 + c22 q2 |
+L+ a2s qs + c2s qs = 0; |
|
|||
&& |
|
&& |
|
&& |
|
|
................................................................................... |
|
|||||
as1q1 |
+ cs1q1 |
+ as2 q2 + cs2 q2 |
+L+ ass qs + css qs = 0. |
|
|
|
|
|
|||||
&& |
|
&& |
|
&& |
|
. |
|
|
|
|
|
|
|
По физической природе выражение [a]q&r& представляетr собой динамическую часть общего усилия,
действующего на элемент динамической системы, а [c]q характеризует ее упругие свойства. Вид коэффициентов
aij и cij зависит от конкретной задачи и способа записи дифференциального уравнения. Например, упомянутый выше прямой способ особенно удобен при изучении колебаний систем цепной структуры, если упругие силы
несложно выражаются через перемещения двух соседних тел.
a)

b)
Рис. 3.4.2
Простейший пример колебательной механической системы с линейными перемещениями масс mi приведен на рис. 3.4.2a. Механическая система, для которой характерно наличие угловых перемещений,
изображена на рис. 3.4.2b. Перемещения, аналогичные схеме “b”, вызываются закручиванием валов - такие
|
|
|
|
|
|
|
|
|
q j |
рассматривать горизонтальное |
||||
колебания называются крутильными. Если в качестве обобщенной координаты |
|
|||||||||||||
перемещение j -го груза в схеме на рис. 3.4.2a или угловое перемещение |
j -го диска в схеме на рис. 3.4.2b, то |
|||||||||||||
сумма упругих сил, действующих на груз (или упругих моментов, действующих на диск), равна |
|
|
||||||||||||
|
|
|
Fj = −k j−1, j (q j − q j−1 )+ k j, j+1 (q j+1 |
− q j ) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
где |
k j−1, j |
- жесткость упругой связи, расположенной между |
j −1 |
-м и |
j |
-м грузами (дисками); |
k j, j+1 |
- |
||||||
жесткость упругой связи, расположенной между j -м и |
j +1-м грузами (дисками). Матрица инерционных |
|||||||||||||
коэффициентов |
[a] видоизменяется для схемы “a” в диагональную матрицу масс |
[m] |
|
|
||||||||||
|
|
|
m1 |
0 |
|
....... |
|
0 |
|
|
|
|
|
|
|
|
|
0 |
m |
|
....... |
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
[m] = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
..... ....... ........ ....... |
|
|
|
|
|||||||
|
|
|
|
0 |
|
....... |
|
ms |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
, |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а для схемы “b” |
- в диагональную матрицу моментов инерции диска [I ]: |
|
|
|
|
|
|
|||||||
|
|
|
I1 |
|
0 |
|
....... |
0 |
|
|
|
|
|
|
|
|
|
0 |
I2 |
|
....... |
0 |
|
|
|
|
|
||
|
|
|
[I ] = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
..... ....... ........ ....... |
|
|
|
||||||||
|
|
|
|
|
0 |
|
....... |
Is |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
. |
|
(3.4.13) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Дифференциальное уравнение движения (3.4.12) приобретает форму:
• |
схема “a” |
m j q&r&j |
= −k j−1, j (q j − q j−1 )+ k j, j+1 (q j+1 |
− q j |
) |
- |
|
|
; |
||
• |
схема “b” |
I j q&r&j |
= −k j−1, j (q j − q j−1 )+ k j, j+1 (q j+1 |
− q j |
) |
- |
|
|
. (3.4.14) |
Решение системы дифференциальных уравнений движения; главные колебания и собственные частоты. Предположим, что обобщенные координаты выбраны таким образом, что они, а следовательно, и определяемые ими перемещения системы, будут изменяться по одному и тому же гармоническому закону, с одной
частотой ω . Система в этом случае совершает гармоническое колебание, и все ее точки одновременно достигают положений наибольшего отклонения и одновременно проходят через положения равновесия. Такие колебания
называются главными. Предположение о том, что все материальные точки системы совершают колебания одной и той же частоты при различных амплитудах, основано на следующем очевидном обстоятельстве: только частота является неотъемлемым свойством системы, тогда как амплитуда зависит от того, как именно эта система приведена в движение внешней причиной.
Система с s степенями свободы в общем случае может совершать s независимых гармонических
колебаний, каждому из которых соответствует определенное значение частоты ωi . Следовательно, колебательный процесс (при условии малости колебаний около положения устойчивого равновесия) в
соответствии с принципом суперпозиции представляет собой линейное наложение s главных гармонических колебаний.
|
Итак, частное решение системы дифференциальных уравнений (3.4.11) будем искать в виде |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
q j |
= Aj sin(ω t +ϕ) |
j =1,2,K, s |
, |
|
|
|
|
|
(3.4.15) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
||
Aj |
- амплитуда |
j |
-го колебания; |
ω |
|
|
|
|
|
|
|
|
|
q j |
. |
|
|
|
|
|
|
|
||||
где |
|
|
|
- частота, общая для всех координат |
|
|
|
|
|
|
|
|
||||||||||||||
|
Подставляя (3.4.15) в (3.4.11), получаем систему s алгебраических уравнений с неизвестными |
Aj и ω : |
||||||||||||||||||||||||
|
|
|
(c11 −ω |
2 |
a11 )A1 |
+ (c12 |
−ω |
2 |
a12 )A2 +K+ (c1s |
−ω |
2 |
a1s )As = 0; |
|
|
||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
(c21 −ω2 a21 )A1 |
+ (c22 −ω2 a22 )A2 |
+K+ (c2s −ω2 a2s )As = 0; |
|
||||||||||||||||||||
|
|
|
............................................................................................... |
|
|
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
(c |
s1 |
−ω |
2 a |
s1 |
)A |
+ (c |
s2 |
−ω2 a |
s2 |
)A |
+K+ (c |
ss |
−ω2 a |
ss |
)A = 0. |
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
s |
|
(3.4.16) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система (3.4.16) однородна относительно неизвестных амплитуд A1 , A2 ,K, As , следовательно, для того чтобы она имела нетривиальное (отличное от нуля) решение, ее определитель должен равняться нулю:
|
c |
|
−ω2 a |
|
c |
|
−ω2 a |
|
L c |
|
−ω2 a |
|
|
|
|
|
|
11 |
11 |
12 |
12 |
1s |
|
1s |
|
|
|
||||||
|
c |
21 |
−ω2 a |
21 |
c |
22 |
−ω2 a |
22 |
L c |
2s |
−ω2 a |
2s |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
.................................................................... |
|
|
|
||||||||||||
|
cs1 −ω2 as1 |
cs2 −ω2 as2 |
L css |
−ω2 ass |
. |
(3.4.17) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Раскрыв определитель (3.4.17), получаем алгебраическое уравнение s -ой степени относительно ω2 |
, |
|||||||||||||||
которое носит название частотного или характеристического (иногда в литературе можно встретить и термин вековое уравнение). Его корни, называемые собственными частотами, определяются только свойствами системы и не зависят от способа приведения этой системы в движение. Если система совершает малые колебания около состояния устойчивого равновесия (т. е. потенциальная энергия системы положительна), то, как следует из теорем
алгебры [14], характеристическое уравнение имеет ровно s корней, причем все они вещественны, положительны и в общем случае различны.
Для уравнений в прямой форме (т. е. типа (3.4.12)) характеристическое уравнение (3.4.17) упрощается: оно приобретает диагональный вид, причем по главной диагонали располагаются члены с квадратами собственных частот,
|
|
|
|
|
c |
|
−ω2 a |
|
|
c |
|
|
|
|
K |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
11 |
|
|
|
|
1 |
|
|
|
12 |
|
|
|
|
|
|
1s |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
c21 |
|
|
|
|
c22 −ω2 a2 |
|
L c2s |
|
|
|
|
|
|
|
= 0 |
|
|
||||||||||
|
|
|
|
|
.................................................................... |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
cs1 |
|
|
|
|
|
|
cs2 |
|
|
L css −ω2 as |
|
|
|
. |
|
(3.4.18) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Запишем, например, характеристическое уравнение для системы, изображенной на рис. 3.4.1, положив |
||||||||||||||||||||||||||||||||||
q1 |
= x1 , q2 = x2 . Подставив в (3.4.3) решение (3.4.15), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
(k11 + k12 − m1ω |
2 |
)A1 |
|
|
− |
|
|
k12 A2 = 0; |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k12 − m2ω |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
− k12 A1 |
|
|
|
|
+ |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)A2 = 0. |
|
(3.4.19) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда характеристическое уравнение записывается как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
(k |
11 |
+ k |
12 |
) − m ω2 |
|
|
|
− k |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
= 0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
− k12 |
|
|
|
|
|
|
k12 − m2ω2 |
|
|
, |
|
|
|
|
|
||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m m |
ω4 |
−{m k |
12 |
+ m |
2 |
(k |
11 |
+ k |
12 |
)}ω |
2 + (k |
11 |
+ k |
12 |
)k |
12 |
− k 2 |
|
(3.4.20) |
|||||||||||||||
|
|
1 |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 , |
|
||||||||||
и имеет два положительных корня |
ω2 |
и |
ω |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
2 . Для того чтобы (3.4.20) согласовывалось с (3.4.18), нужно положить |
|||||||||||||||||||||||||||||||||
a1 |
= m1 ; a2 = m2 ; c11 = k11 + k12 ; |
|
c22 = k12 ; c12 |
= −k12 . Таким образом, матрица жесткости |
[c] и |
||||||||||||||||||||||||||||||
матрица инерционных коэффициентов [a] для рассматриваемого примера имеют вид |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
+ k |
|
|
− k |
|
|
|
|
|
|
|
m |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
[c]= |
11 |
|
|
12 |
|
|
12 |
|
[a]= |
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− k12 |
|
|
k12 |
; |
|
|
|
|
|
|
0 m2 |
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Собственные формы. Как было показано выше, в результате решения характеристического уравнения |
||||||||||||||||||||||||||||||||||
(3.4.1) определяется спектр собственных частот рассматриваемой системы, ω1 <ω2 |
<K<ωs (корни |
||||||||||||||||||||||||||||||||||
принято располагать в порядке возрастания). Зная собственные частоты, можно перейти к решению уравнений
(3.4.16). Подставив в (3.4.16) одно из найденных значений квадрата частоты, например ωi2 , получим систему s
линейных однородных уравнений относительно амплитуд A1i , A2i ,K, Asi (здесь первый индекс обозначает номер координаты, а второй - номер собственной частоты). Из общих свойств однородных систем линейных
алгебраических уравнений [6, 14] следует, что ранг матрицы полученной системы равен s −1 (так как равные корни по предположению отсутствуют). Это означает, что из s уравнений системы независимыми являются только
s −1. Поскольку s −1 уравнений связывают между собой s амплитуд, все амплитуды можно выразить через какую-либо одну, например через первую, значение которой произвольно:
λ 1i = const; λ 2i = |
A2i |
; |
λ 3i = |
A3i |
; K, λ si = |
Asi |
. |
|
|
|
|
|
|||||
|
A1i |
|
A1i |
A1i |
(3.4.21) |
|||
Aji
Совокупность соотношений (3.4.21) позволяет находить, таким образом, не сами амплитуды Aji
рассматриваемой i -ой гармоники, а их относительные значения λji , определенные с точностью до
произвольного множителя, т. е. описывает конфигурацию системы в процессе свободных колебаний с i -ой собственной частотой. Такие конфигурации, число которых равно числу степеней свободы системы,
характеризующие свойства самой системы и не зависящие от начальных условий, называются собственными формами. Каждому корню характеристического уравнения (3.4.17) соответствует своя собственная форма (3.4.21).
Поскольку коэффициенты собственных форм λ ji вычисляются с точностью до произвольного множителя, можно один из коэффициентов положить равным какому-либо числу, например единице, а можно выбрать его таким
образом, чтобы сумма квадратов амплитуд рассматриваемой формы равнялась единице (в этом случае форма
называется нормированной). Если принять λ 1i =1, то общее решение уравнения (3.4.11), представляющее собой сумму частных, имеет вид
s |
|
|
|
|
|
|
q j = ∑λ ji A1i sin(ω i t +ϕ i ) |
|
i, j =1,2,K, s |
|
λ 1i =1 |
|
|
i=1 |
, |
, |
. |
(3.4.22) |
||
|
|
|
Решение (3.4.22) содержит 2s произвольных постоянных ( s амплитуд A1i и s начальных фаз ϕi ), которые находятся из начальных условий, в качестве которых, как правило, используются значения обобщенных
|
& |
|
t = 0 : |
|
|
|
|
координат qi и обобщенных скоростей qi в момент времени |
|
|
|
|
|||
|
|
s |
|
|
|
|
|
|
q j |
(0) = ∑λ ji |
A1i sin ϕ i |
; |
|
|
|
|
|
|
|
||||
|
|
i=1 |
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
(0) = ∑λ ji |
|
|
|
|
|
|
A1iω i cosϕ i . |
|
|
||||
|
q j |
j =1,2,K, s . |
|
||||
|
|
i=1 |
|
|
, |
(3.4.23) |
|
Собственные формы обладают важным свойством ортогональности: если Arn и Arm - системы |
|
||||||
амплитуд, соответствующие n |
-ой и m -ой произвольным собственным формам, то они связаны соотношением |
||||||
|
|
s |
s |
|
|
|
|
|
|
∑Arn ∑a jr Ajm |
= 0 |
|
|
||
|
|
r=1 |
j=1 |
|
. |
|
(3.4.24) |
|
|
|
|
|
|
||
a jr |
= 0, j ≠ r |
, т. е. для прямых уравнений, (3.4.24) приобретает более простой |
|||||
В том случае, когда |
|
||||||
вид, |
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
∑ar Arm Arn |
= 0 |
|
|
||
|
|
r=1 |
|
|
. |
|
(3.4.25) |
Доказательство свойства ортогональности выходит за рамки настоящей книги.
Введенное выше понятие собственных форм позволяет сформулировать важное утверждение: любую форму колебаний можно разложить по собственным формам некоторой системы с s степенями свободы. Это
означает, что любую заданную мгновенную совокупность s обобщенных координат B1 , B2 ,K, Bs |
можно |
|
представить линейными комбинациями вида |
|
|
s |
|
|
B j = ∑µ i A ji |
, j =1,2,K, s . |
|
i=1 |
(3.4.26) |
|
Справедливость этого утверждения следует непосредственно из первых s уравнений (3.4.23), которые

только обозначениями отличаются от (3.4.26), и теоремы существования общего интеграла системы
дифференциальных уравнений [34]. Коэффициенты µ i вычисляются с помощью свойства ортогональности
(3.4.24) или (3.4.25).
В качестве примера найдем собственные частоты и собственные формы для системы, изображенной на
рис. 3.4.1, приняв для простоты k11 = k12 = k; m1 |
= m2 |
= m. Тогда дифференциальные уравнения (3.4.19) |
|||||||||||||||||
преобразуются как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(2k − mω |
2 |
)A1 |
|
− |
|
|
|
|
|
kA2 = 0; |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k − mω |
|
|
|
|
|
|
|
− kA1 |
|
+ |
|
|
|
|
2 |
|
|
(3.4.27) |
|||||||
|
|
|
|
|
|
|
|
)A2 = 0. , |
|||||||||||
а характеристическое уравнение (3.4.20) - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2k − mω2 |
|
|
|
|
|
|
|
− k |
|
|
= 0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
− k |
|
|
|
|
|
|
k − mω2 |
|
||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
k |
4 |
−3 |
k |
ω |
2 |
+ |
k 2 |
|
= 0. |
|
|
|
|
||||
|
|
|
|
m |
|
m2 |
|
|
|
|
(3.4.28) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
ω1,22 = |
|
k (3 ± 5 ) |
|
|
|||||
Решением биквадратного уравнения (3.4.28) являются числа |
|
|
|
|
2m |
|
|
, или приближенно |
|||||||||||
ω12 = 0,38 |
k |
, |
ω22 |
= 2,62 |
|
k |
|
|
|
|
|
||||||||
|
|
m . |
|
|
|
|
|||||||||||||
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
(3.4.29) |
|||||
Приняв λ11= λ12 =1, остальные коэффициенты собственных форм определим с помощью любого из уравнений (3.4.27):
λ 21= |
2k − mω2 |
=1,62 λ 22 = |
2k − mω2 |
= −0,62 |
|
1 |
2 |
|
|||
k |
k |
|
|||
|
; |
. |
(3.2.30) |
Собственные формы приведены на рис. 3.4.3.
Рис. 3.4.3
В заключение запишем полученные выше соотношения в матричной форме. Решение уравнения (3.4.10) будем искать в виде
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
|
rT |
q = |
Asin(ωt +ϕ) |
, |
|
|
|
(3.4.31) |
|
|
r |
|
|
|
|
|
|
|
|||
|
|
= {A1 |
|
|
r |
|
|
|
|||
где |
A - матрица - столбец амплитуд, так что A |
, A2 ,K, As }, AT |
- матрица, транспонированная по |
||||||||
|
r |
|
|
|
|
|
|
|
|
|
|
отношению к A . Подставляя (3.4.31) в (3.4.10), получаем матричное уравнение |
|
|
|
||||||||
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
|
|
−[a]Aω2 + |
[c]A = 0 |
, |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
([c]−[a]ω |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
r |
|
2 )A = 0 |
. |
|
|
|
(3.4.32) |
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрица столбец |
A отлична от нуля, когда выполняется условие |
|
|
|
|
|
||||
|
|
|
|
det([c]−[a]ω2 )= 0 |
, |
|
|
(3.4.33) |
|||
|
|
|
|
|
|
|
|
|
|
||
которое полностью совпадает с характеристическим уравнением (3.4.17). Умножим (3.4.32) слева на [a]−1 |
и |
||||||||||
перенесем один из членов через знак равенства. Получим |
r |
r |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
[a]−1 [c]A =ω2 A . |
|
|
|
(3.4.34) |
|||
|
Из теории матриц известно, что ω2 |
|
|
|
|
|
|
−1 |
[c], а вектор |
r |
|
|
является собственным числом матрицы −[a] |
A - ее |
|||||||||
собственным вектором (или собственным значением).
Свободные колебания с сопротивлением. Остановимся кратко на рассмотрении колебаний при условии действия сил сопротивления. Предположим, что действующие на механическую систему силы сопротивления являются линейными функциями обобщенных скоростей - во многих задачах механики это допущение оправдано. Тогда дифференциальные уравнения движения (3.4.10) принимают вид
|
|
[a]q&r&+[b]q&r&+[c]qr = 0 , |
|
|
(3.4.35) |
|||
или |
|
|
|
|
|
|
|
|
s |
(a jk qk +bjk qk + c jk qk )= 0 |
|
|
|
||||
∑ |
|
|
|
|||||
|
|
&& |
& |
|
|
, j =1,2,K, s , |
|
|
k =1 |
|
|
|
|
|
(3.4.36) |
||
где [b] - матрица демпфирования, равная |
|
|
|
|
|
|
|
|
|
|
b |
b |
....... |
b |
|
|
|
|
|
11 |
12 |
|
1s |
|
|
|
[b]= |
b21 |
b22 |
....... |
b2s |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
..... ....... ........ ....... |
|
|
||||
|
|
|
bs2 |
....... |
bss |
|
|
|
|
|
bs1 |
|
. |
(3.4.37) |
|||
|
|
|
|
|
|
|
||
Решение системы (3.4.36) ищем в виде |
|
|
q j = Aj exp(pt) |
|
|
|
||
|
|
|
|
|
(3.4.38) |
|||
|
|
|
|
|
, |
|
|
|
причем в общем случае p принадлежит ко множеству комплексных чисел, т. е. |
p =α +iβ . Подстановка |
|||||||
