
Основы проектирования машин / ГЛАВА 3.1. ОБЩИЙ СЛУЧАЙ РАСЧЕТА НАПРЯЖЕННО - ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ
.pdf
ГЛАВА 3.1. ОБЩИЙ СЛУЧАЙ РАСЧЕТА НАПРЯЖЕННО - ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
Три группы основных уравнений. Рассмотренные ранее частные случаи определения напряжений ( глава 2.7 ) и деформаций (глава 2.6 ) следует дополнить решением задач теории упругости в общем виде. Теорией упругости называется раздел механики сплошной среды, который занимается изучением поведения упругих твердых тел при их нагружении. При этом деформируемая среда считается однородной и изотропной, т. е. ее упругие свойства одинаковы во всех направлениях. Кроме того, предполагается, что среда деформируется линейно (для материала среды выполняется закон Гука), причем перемещения и деформации достаточно малы.
В общем случае расчет напряженно - деформированного состояния в точке (т. е. расчет на прочность и жесткость) можно провести с помощью системы фундаментальных уравнений теории упругости. Получение точного аналитического решения этих уравнений оказывается достаточно сложной процедурой. По этой причине аналитические методы имеют ограниченное применение. Единственным выходом из такого положения является использование приближенных численных методов, реализация которых возможна с помощью современной вычислительной техники. С помощью численных методов решения фундаментальных уравнений теории упругости можно выполнить все необходимые вычисления для корректного описания напряженно - деформированного состояния бесконечно большого числа возможных вариантов конструкций при произвольном нагружении и закреплении (см. далее главу 3.3 ). С этой целью разрабатывается специализированное программное обеспечение, позволяющее решать комплекс этих и смежных с ними задач.
Перейдем теперь к непосредственному выводу уравнений, являющихся основанием для анализа напряженно - деформированного состояния в точке численными методами. Эти уравнения можно разделить на три группы.
Первая группа, или статические уравнения, описывает равновесие выделенного в окрестности некоторой точки тела элементарного параллелепипеда. Вторая группа уравнений, или обобщенный закон Гука, выражает зависимость между напряжениями и деформациями элемента. Поскольку в этих уравнениях учитываются физико - механические свойства материала, их называют физическими. Наконец, уравнения третьей группы связывает деформации элемента тела с перемещениями его точек вследствие действия приложенной нагрузки - это
геометрические уравнения.
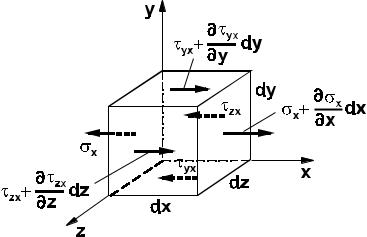
Уравнения равновесия элемента объема. Рассмотрим некоторое тело, нагруженное произвольной системой сил (рис. 2.7.1). Для анализа напряженно - деформированного состояния тела в окрестности произвольно
выбранной точки A вырежем элемент объема, имеющий форму параллелепипеда со сторонами dx, |
dy и dz . |
|||||||||||
По граням этого выделенного элемента в общем случае трехосного нагружения действуют нормальные и |
||||||||||||
касательные напряжения (рис. 3.1.1), которые можно представить в форме тензора напряжений [σ] |
следующего |
|||||||||||
вида: |
|
|
|
|
|
|||||||
|
|
|
|
|
σx |
τyx |
τzx |
|
|
|||
|
|
|
|
|
|
σ y |
|
|
|
|||
|
|
|
[σ]= τxt |
τzy |
|
|
||||||
|
|
|
|
|
|
τyz |
|
|
|
|||
|
|
|
|
|
τxz |
σz |
. |
(3.1.1) |
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.1.1
Напомним, что первый индекс в обозначениях напряжений указывает площадку, на которой действует напряжение, а второй - его направление; поскольку в обозначениях нормальных напряжений фигурируют два одинаковых индекса, обычно один из них опускают.
Согласно закону парности касательных напряжений (2.4.14), имеют место равенства
τxy |
= τyx |
; |
τ |
xz |
= τ |
zx ; |
τyz |
= τzy |
. |
(3.1.2) |
|
|
|
|
|
|
Поскольку, как следует из (3.1.2), матрица напряжений (3.1.1) симметрична, в механике вводят вектор -
столбец напряжений σr, который записывается как
σrT = [σx σ y |
σz τxy |
τzx |
τ yz ] |
(3.1.3) |
|
|
|
. |
Здесь и далее верхний индекс “ T ” означает транспонирование вектора, что позволяет для сокращения записывать его в строку, а не в столбец.
Кроме напряжений, приложенным к граням, в общем случае на выделенный элемент объема могут
действовать массовые силы, компоненты которых в проекции на координатные оси обозначим как X , Y и Z . Примерами массовых сил могут служить сила тяжести, центробежные нагрузки, а также некоторые другие силы,
которые равномерно распределены в объеме рассматриваемого тела.
Рис. 3.1.2
Ясно, что после приложения внешней нагрузки выделенный элемент объема находится в равновесии. Аналитически условие равновесия можно получить, спроектировав все силовые факторы на оси координат.
Выполним операцию проектирования, например, на ось x . С этой целью на рис. 3.1.2 изображены только те силовые факторы, которые направлены вдоль этой оси. Тогда имеем
|
|
|
∂ σ |
x |
|
|
|
|
|
|
|
|
∂ τ |
yx |
|
|
|
|
σ |
|
+ |
|
|
dx dydz −σ |
|
dydz + τ |
|
+ |
|
dy dxdz −τ |
|
dxdz + |
|||||
|
∂ x |
|
|
|
|
|
||||||||||||
|
x |
|
|
|
x |
|
|
|
yx |
|
∂ y |
|
zx |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ τ |
zx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
+ |
|
|
dz dxdy −τ |
|
|
dxdy + Xdxdydz = 0. |
|
|
|
|||||||
|
∂ z |
|
|
|
|
|
|
|||||||||||
|
zx |
|
|
|
yx |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисляя аналогично (3.1.4) суммы проекций сил на оси |
y и z , после приведения подобных членов и |
|||||||||||||||||
деления на dV = dxdydz окончательно получаем систему дифференциальных уравнений равновесия Навье, а
именно
∂ σ |
x |
|
|
|
∂ τ |
|
yx |
|
|
|
∂ τ |
|
zx |
|
|
|
||||||||
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
+ X = 0 |
||||||||||
|
∂ |
x |
|
∂ |
y |
|
|
∂ |
|
z |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∂ τ |
|
xy |
|
|
+ |
|
∂ σ |
y |
|
|
+ |
|
∂ τ |
|
zy |
|
+Y = 0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∂ |
|
x |
|
|
|
∂ |
|
y |
|
|
|
∂ |
zy |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∂ τ |
|
xz |
|
+ |
|
∂ τ |
yz |
|
+ |
|
∂ σ |
z |
|
+ Z = 0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
∂ |
|
x |
|
|
∂ |
|
y |
|
|
∂ |
|
|
z |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Уравнения равновесия (3.1.5) удобно записать в матричной форме,
[A]σr + gr = 0 ,
(3.1.5)
(3.1.6)
где элементы матрицы [A] представляют собой операторы дифференцирования, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
∂ |
0 |
|
0 |
|
∂ |
|
|
∂ |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
∂ |
x |
|
∂ |
y |
|
∂ |
z |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
[A] |
|
|
|
|
|
∂ |
|
|
|
∂ |
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
∂ y |
|
∂ |
x |
|
|
|
|
∂ |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
∂ |
|
|
|
|
z |
|
|
|
|
|
||||||||
|
|
|
|
|
|
0 |
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
∂ |
z |
|
|
|
∂ |
x |
|
∂ |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
, |
|
(3.1.7) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а матрица - столбец |
gr |
состоит из компонент массовых сил: |
grT |
= [X Y Z ] |
. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Сформулируем теперь условия на поверхности тела как граничные условия для дифференциальных |
|
|
||||||||||||||||||||||||||||
уравнений (3.1.5). Они выражают равновесие между поверхностной нагрузкой и напряжениями в произвольной |
|
||||||||||||||||||||||||||||||
точке поверхности тела. Пусть на произвольно ориентированную площадку dA |
в трехмерном пространстве |
|
|
||||||||||||||||||||||||||||
действует некоторая внешняя поверхностная нагрузка Pr (рис. 3.1.3a), |
PrT = [px |
|
py |
pz ], где |
px , |
py |
и |
||||||||||||||||||||||||
pz |
- проекции на координатные оси вектора полной внешней поверхностной нагрузки Pr. Проекции |
px , |
py |
и |
|||||||||||||||||||||||||||
pz |
определяются из уравнений равновесия тетраэдра OABC . Массовые силы в большинстве случаев |
|
|
||||||||||||||||||||||||||||
оказываются малыми, и их наличием можно пренебречь. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Ориентация рассматриваемой площадки описывается значениями направляющих косинусов, т. е. косинусов |
||||||||||||||||||||||||||||||
углов между направлением вектора нормали nr |
к площадке и соответствующими ортами декартовой системы |
|
|||||||||||||||||||||||||||||
координат (рис. 3.1.3b), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
r |
r |
|
m |
|
r |
|
r |
|
|
|
|
r |
, |
r |
|
|
|
|
|
|
|
|
||||||
|
|
|
l = cos i , |
n |
|
= cos j |
, |
n |
|
t = cos k |
|
n |
|
|
|
|
|
=1 . |
|
|
|||||||||||
|
|
|
|
|
|
; |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
; |
l 2 |
|
+ m2 +t 2 |
(3.1.8) |
||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
|
|
|
|
|
|
b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.1.3. |
|
|
|
|
|
||||||
Составим сумму проекций всех сил, приложенных к граням тетраэдра, на ось Ox (на рис. 3.1.3b показаны только те напряжения, которые дают проекции на эту ось):
откуда
py и
px dA −σx ldA −τyx mdA −τzxtdA = 0 ,
σxl +τyx m +τzxt = px .
Аналогично, проектируя все действующие на тетраэдр силы на оси Oy и Oz , находим выражения для pz . В результате получаем следующие формулы для составляющих полной поверхностной нагрузки:
σxl +τyx m +τzxt = px |
|
|
|
|
|
|
|
τxy l +σ y m +τzy t = py |
|
|
|
|
|
|
|
τxz l +τyz m +σz t = pz |
. |
(3.1.9) |
|
|
|
||
В сокращенной записи условия на поверхности (3.1.19) представляются в виде
|
|
|
l |
0 |
0 |
m t 0 |
|
|
|
|
|
|
[L]= 0 m 0 |
l 0 t |
|
|
|
||
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[L]σ = P |
, |
0 0 |
t 0 l m |
. |
(3.1.10) |
||||
|
|
|
|
|
|
|
|||
Закон Гука. Для случая объемного напряженного состояния линейно-упругих изотропных тел справедлив обобщенный закон Гука (2.7.8), который в матричном виде выглядит как
|
|
|
εx |
|
|
|
|
|
|
|
|
|
|
|
εy |
|
|
|
|
r |
|
|
|
|
|
εz |
|
|
|
|
|
ε |
= |
|
|
|
|
|
γ xy |
|
|
|
|
|
|
|
|
r |
−1 r |
|
γ zx |
|
|
|
γ |
|
|
||
ε =[E] |
σ |
|
|
|
|
; |
yz |
; |
|||
|
|
|
|
||
|
|
|
|
|
|
1 / E − µ / E − µ / E 0 |
0 |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
1 / E |
− µ / E |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
− µ / E |
|
|
|||||||
|
|
|
[E]−1 = − µ / E − µ / E 1 / E |
0 |
0 |
0 |
|
|
|||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
0 |
0 |
0 |
1 / G |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 / G |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
1 / G |
. (3.1.11) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь модули упругости E и G связаны между собой соотношением (2.4.11); матрица упругой |
|
|
|||||||||||||
податливости [E]−1 |
является обратной по отношению к матрице модулей упругости (или матрице жесткости) [E] |
||||||||||||||
, которая в свою очередь равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
(1 − µ) |
µ |
µ |
0 |
|
0 |
0 |
|
|
||
|
|
|
|
|
|
µ |
(1 − µ) |
µ |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
µ |
µ |
(1 − µ) |
0 |
|
0 |
0 |
|
|
|
|
|
E |
|
|
|
|
|
|
|
(1 − 2µ) |
|
|
|
|
|
[E] = |
|
|
|
|
0 |
0 |
0 |
|
|
0 |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
(1 + µ)(1 |
− |
|
2 |
|
|
||||||||||
|
2µ) |
|
|
|
(1 − 2µ) |
|
|
|
|||||||
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
(1 − 2µ) |
||||
|
|
|
|
|
|
|
0 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Уравнения (3.1.11), называемые законом Гука в прямой форме, дают возможность вычислить деформации, если известны напряжения. В ходе решения задач теории упругости часто возникает необходимость в обратных соотношениях, когда напряжения выражены через деформации. Для этого надо разрешить уравнения (3.1.11) относительно напряжений. Получим
σr = [E]εr,
или
σ |
|
= |
|
|
E |
|
[(1 − µ)ε |
|
|
x |
(1 |
+ µ)(1 − 2µ) |
x |
||||||
|
|
|
|
||||||
σ y = |
|
E |
|
[(1 − µ)εy |
|||||
(1 |
+ µ)(1 − 2µ) |
||||||||
|
|
|
|
|
|
||||
σz |
= |
|
|
E |
|
[(1 − µ)εz |
|||
|
(1 |
+ µ)(1 − 2µ) |
|||||||
|
|
|
|
|
|
||||
τxy = Gγ xy ; τyz = Gγ yz ; τzx
+ µ(εy +εz )] |
|
|
|
|
|
+ µ(εx +εz )] |
|
|
|
|
|
+ µ(εx +εy )] |
|
|
|
|
|
= Gγ zx . |
|
|
|
(3.1.12) |
|
|
. |
|
Равенства (3.1.12) выражают обратную форму закона Гука.
Поля упругих перемещений точек элемента при нагружении. Внешние нагрузки, приложенные к телу, вызывают деформирование этого тела и перемещение составляющих его точек в пространстве (рис. 2.1.3).
Определим соотношения, связывающие абсолютные перемещения точек тела с их относительными смещениями , или деформациями.
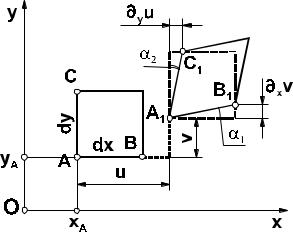
Рис. 3.1.4 |
Представим трехмерную задачу как совокупность плоских проекционных - такой подход позволяет существенно упростить картину без ограничения общности. На рис. 3.1.4 изображено положение некоторого
элемента плоскости XOY до приложения нагрузки и после. Примем за начало отсчета деформаций точку A с
координатами ( x A , yA ), а конечное положение этой точки обозначим через A1 , так что компоненты линейного
перемещения точки A по направлениям координатных осей равны как u и v . Будем считать, что эти компоненты являются малыми величинами, меняющимися непрерывно по объему тела; деформациями, связанными с
искривлением ребер выделенного элемента, пренебрегаем. Если тело подвергается деформации, то в условиях принятых допущений при переходе от точки A к соседней точке B , расположенной на оси x , изменяется только абсцисса на величину dx , так что перемещения точки B отличаются от перемещений точки A на величины
частных приращений ∆xu и ∆x v , которые можно приближенно заменить частными дифференциалами (линейными частями приращений)
|
|
∂ |
x |
u = |
∂u dx; |
∂ |
x |
v |
= ∂v dx |
|
|
|
|
|
|
||
|
|
|
|
|
∂x |
|
|
|
∂x . |
|
|
|
|
|
|
||
Тогда перемещения точки B с точностью до величин первого порядка малости по dx имеют вид |
|
||||||||||||||||
|
|
|
|
u + |
∂u dx; |
v + |
∂v dx |
|
|
|
|
|
|
||||
|
|
|
|
|
|
∂x |
|
|
|
|
∂x . |
|
|
|
|
|
|
Таким образом, абсолютное увеличение длины ребра AB , вызванное деформацией, равно |
∂u dx |
||||||||||||||||
∂x |
, а |
||||||||||||||||
|
A в направлении x (т. е. линейная деформация) составляет |
ε |
x |
= ∂u |
|
||||||||||||
относительное удлинение в точке |
|
∂x . |
|||||||||||||||
Аналогично можно рассмотреть перемещения точки C (равные |
u + ∂u dy; |
v + ∂v dy |
|
|
|
|
|||||||||||
∂y |
∂y |
) и линейную |
|
||||||||||||||
|
y |
|
|
ε |
y |
= ∂u |
|
|
|
|
|
|
|
|
|
|
|
деформацию в направлении оси |
, равную |
∂y |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Угловая деформация выделенного элемента, в соответствии с (2.1.5), определяется как уменьшение первоначально прямого угла CAB . И рисунка (3.1.4) видно, что это уменьшение равно сумме углов поворотов ребер α1 и α2 . Поскольку углы малы, то
α1 ≈ tgα1 = |
∂ |
v |
|
∂v |
|
α2 ≈ tgα1 = |
∂y u |
|
∂u |
|
x |
|
= |
|
; |
|
= |
|
|||
dx |
∂x |
dy |
∂y . |
|||||||
|
|
|
|
|
||||||
Следовательно, для угловой деформации γ xy получаем
γ xy = tgα1 +tgα2 = |
∂ u |
+ |
∂ v |
|
|
|
|
||
∂ y |
∂ x |
|
||
|
|
|
. |
|
Для общего трехмерного случая выражения, связывающие абсолютные и относительные перемещения, имеют вид
ε |
x |
= |
∂u ; |
|
ε |
y |
= |
∂v |
; |
|
ε |
z |
= |
∂w ; |
|
||
|
|
∂x |
|
|
|
∂y |
|
|
|
|
|
∂z |
|
||||
γ |
xy |
= |
∂u |
+ |
∂v |
; |
γ |
zx |
= |
∂w |
+ ∂u |
; |
|||||
|
|
∂y |
|
∂x |
|
|
|
∂x |
|
∂z |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ = ∂v |
|
|
|
|
|
+ |
∂w |
|
|
||
yz |
|
|
|
|
|
∂z |
|
∂y |
|
|
|
|
|
. |
(3.1.13) |
||
|
|
|
|
||
Соотношения (3.1.13) называются геометрическими уравнениями Коши. В матричной форме они
записывается как |
|
|
|
εr = [A]T ur. |
(3.1.14) |
Здесь [A]T получена транспонированием матрицы [A], введенной в (3.1.7), а векторы - столбцы |
|
|
перемещений ur равен urT = [u v w] |
, а вектор - столбец деформаций εr определяется (3.1.11). |
|
Иногда вместо (3.1.13) удобнее использовать так называемые уравнения сплошности (неразрывности), или уравнения совместности деформаций, которые представляют собой иную форму записи геометрических уравнений. Согласно уравнениям сплошности, при деформациях сохраняются первоначальные геометрические связи между соседними точками тела. Это обстоятельство подчеркивает отсутствие разрывов связей при упругих перемещениях.
Для вывода уравнений сплошности исключим из уравнений Коши (3.1.13) перемещения u, v и w . |
|||||||||||||||||||||||||||||||
Продифференцируем в (3.1.13) первое уравнение по y |
, а второе - по x , и сложим результаты. Получим |
||||||||||||||||||||||||||||||
|
|
∂ 2εx ∂ 2εy |
∂ 3u |
|
|
|
|
|
∂ 3 v |
|
|
|
∂ |
|
|
|
∂ u |
|
∂ |
v |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ y2 + ∂ x2 = ∂ x∂ y2 + ∂ x2∂ y |
= ∂ x∂ |
|
y |
∂ y |
+ ∂ |
x |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. (3.1.15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнивая (3.1.15) и (3.1.13), замечаем, что в выражение, стоящее в скобках в правой части (3.1.15), равно |
|||||||||||||||||||||||||||||||
угловой деформации |
γ xy |
, поэтому имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
∂ 2ε |
x |
+ |
∂ |
2ε |
y |
= |
|
∂ 2γ |
xy |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
∂ |
y2 |
∂ |
x2 |
|
∂ x∂ |
y |
. |
|
|
|
|
|
|
(3.1.16) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
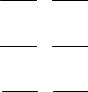
В результате подобных операций можно записать и другие аналогичные (3.1.16) соотношения первой группы условий совместности деформаций Сен-Венана:
∂2εx
∂y2
∂2εy
∂z 2
∂2εz
∂x2
+∂ 2εy
∂x2
+∂ 2εz
∂y2
+∂ 2εx
∂z 2
= |
∂ 2γ |
xy |
|
|
|
|
|
|
|
|
|
|
|
||
∂ |
x∂ |
|
|
|
|
||
|
|
y |
|
||||
= |
∂ 2γ |
yz |
|
|
|
|
|
|
|
|
|
|
|
||
∂ |
y∂ |
|
|
|
|||
|
z |
|
|||||
= |
∂ 2γ |
zx |
|
|
|
|
|
|
|
|
|
|
|
||
∂ |
z∂ |
|
|
|
|
||
|
|
x |
(3.1.17) |
||||
|
|
|
|
|
|
. |
|
Выражения (3.1.17) устанавливают связь между компонентами линейных деформаций в проекционных плоскостях. Угловые деформации в проекционных плоскостях также связаны между собой. Для выявления этих
связей преобразуем в (3.1.13) компоненты угловых деформаций по следующему правилу: дифференцируем γ xy
по z , γzx - по y , а γ yz |
- по x . Сложение первых двух результатов дифференцирования и последующее |
|
||||||||||||||||||||||
вычитание третьего дает |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ γ xy |
+ |
∂ γ |
zx |
− |
|
∂ γ yz |
= 2 |
|
∂ 2u |
|
|
|
|
||||
|
|
|
|
|
|
|
∂ z |
∂ y |
|
∂ x |
∂ y∂ z . |
(3.1.18) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Еще раз дифференцируя обе части равенства (3.1.18) по x и принимая во внимание, что согласно (3.1.13) |
||||||||||||||||||||||||
∂ |
u = ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
верно равенство ∂ |
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, запишем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
∂ |
|
|
∂ γ xy |
|
∂ γ |
zx |
|
∂ γ yz |
|
|
|
∂ 2 |
ε |
x |
|
|
|||||
|
|
|
|
|
|
|
|
|
+ |
|
− |
|
|
|
|
= 2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
∂ |
|
|
|
∂ z |
|
∂ y |
|
|
∂ x |
|
|
|
∂ y∂ z |
|
|||||||
|
|
|
x |
|
|
|
|
|
|
|
(3.1.19) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
По аналогии с (3.1.19) можно определить и остальные соотношения, совокупность которых описывает связи между компонентами деформаций в разных плоскостях:
∂ |
|
|
|
∂ |
γ xy |
|
|
∂ |
γ |
|
|
|
∂ |
γ yz |
||||
|
|
|
|
|
|
|
|
+ |
|
|
|
zx |
− |
|
|
|
||
∂ |
|
|
|
|
∂ |
z |
|
|
|
∂ |
|
y |
|
∂ |
|
x |
||
x |
|
|
|
|
|
|
|
|||||||||||
∂ |
|
|
|
|
∂ γ yz |
|
|
|
∂ γ xy |
|
∂ γ zx |
|||||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∂ |
|
|
|
|
∂ |
x |
|
|
|
∂ |
|
z |
|
∂ |
|
y |
||
y |
|
|
|
|
|
|
|
|||||||||||
∂ |
|
|
|
∂ |
γ zx |
|
|
|
∂ |
γ |
yz |
|
∂ |
γ |
xy |
|||
|
|
|
+ |
|
|
|
− |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∂ |
|
|
|
|
∂ |
y |
|
|
|
∂ |
x |
|
∂ |
|
z |
|||
z |
|
|
|
|
|
|
||||||||||||
|
|
|
∂ |
2 |
εx |
|
|
|
|
|
= 2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
∂ |
y∂ |
z |
|
||||
|
|
|
|||||||
|
|
|
∂ |
2 |
εy |
|
|
|
|
|
|
|
|
|
|
|
|||
|
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
∂ |
z∂ |
x |
|
|||
|
|
|
|
||||||
|
|
|
∂ |
2 |
εz |
|
|
|
|
|
= 2 |
|
|
|
|
|
|
||
∂ |
x∂ |
|
|
|
|||||
|
|
y |
|
||||||
|
|
|
|
|
|
|
|
. |
(3.1.20) |
Если уравнения сплошности (3.1.20) выполняются, то это указывает на отсутствие разрывов упругого тела, что является непременным условием существования прочности упругих тел.
Полная систему уравнений теории упругости. Итак, полную систему уравнений теории упругости составляют: уравнения равновесия Навье (3.1.5) - (3.1.6), закон Гука в прямой (3.1.11) и обратной (3.1.12) формах, а также геометрические уравнения Коши (3.1.13) или эквивалентные им уравнения совместности деформаций Сен-Венана (3.1.20). Заметим, что эта система почти не содержит факторов, определяющих напряженно-деформированное состояние тела, как то: форма и размеры тела, способы его нагружения и закрепления и т. д.
Таким образом, полная система уравнений теории упругости устанавливает лишь общие закономерности, присущие поведению твердого упругого тела под действием внешнего нагружения. Решение же каждой конкретной задачи невозможно без задания некоторых дополнительных (т. н. граничных) условий, определяющих конкретные режимы нагружения и закрепления тела определенных формы и размеров.
Энергетические уравнения. В случае объемного деформирования энергия U0 , накопленная в единице объема, как следует из (2.7.13), равна
U0 = |
dU |
= |
1 |
(σxεx +σ yεy +σzεz +τxyγ xy +τyzγ yz +τzxγ zx ) |
|
|||||||||||
dxdydz |
2 |
, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U0 = |
1 |
|
rT |
r |
|
|
|
|
|||
|
|
|
|
|
|
|
|
σ |
ε |
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
(3.1.21) |
||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||
Здесь σrT |
- матрица - строка, транспонированная по отношению к (3.1.2). Выражение (3.1.21) называется |
|||||||||||||||
формулой Клапейрона. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Потенциальная энергия деформации U всего объема определяется интегрированием (3.1.21) по объему |
||||||||||||||||
|
|
|
|
|
U = |
|
|
|
|
U0dV = |
|
1 |
σrT εr |
|
||
|
|
|
|
|
∫∫∫ |
∫∫∫2 |
|
|||||||||
|
|
|
|
|
|
|
V |
|
|
V |
. |
(3.1.22) |
||||
Работа внутренних напряжений вызвана внешними силовыми факторами, которые приложены к поверхности рассматриваемогоr тела. Пусть на поверхности тела действуют внешние распределенные нагрузки Pr
и массовые силы g . В отличие от внутренних внешние силы в процессе деформирования считаются неизменными
, поэтому при вычислении потенциальной энергии системы W , ответственной за совершение работы внешними силовыми факторами, множитель 1/ 2 будет отсутствовать:
W = −∫∫(Pxu + Py v + Pz w)dA − ∫∫∫(Xu +Yv + Zw)dV
A |
|
|
V |
|
. |
(3.1.23) |
Полная потенциальная энергия системы равна сумме потенциальной энергии деформаций (3.1.22) и работе |
||||||
внешних сил (3.1.23), так что в матричной форме имеем |
|
|
|
|
|
|
∏ =U +W = ∫∫∫ |
1 |
σrT εr |
dV − ∫∫pT urdA − ∫∫∫grT urdV |
|
|
|
2 |
|
|
||||
V |
|
A |
V |
. |
(3.1.24) |
|
|
|
|||||
Плоский случай нагружения. Практический интерес представляет плоский случай нагружения. Двухосным, или плоским называется такое напряженное состояние тела, при котором во всех его точках одно из
напряжений (например, σz ) равно нулю. При этом оказывается, что во всех поперечных сечениях тела
σz = 0; τyz =τzx = 0 ,
а напряжения σz , τxy =τyx =τ изменяются в зависимости от z в соответствии с законом распределения внешнего нагружения.
Такое напряженное состояние приблизительно осуществляется в тонких пластинах, подвергающихся действию сил, не вызывающих изгиб, т. е. лежащих в срединной плоскости пластины.
Если плоское напряженное состояние возникло под действием равномерно распределенной по длине
нагрузки, то все не равные нулю напряжения не будут зависеть от переменной z . Тогда основные уравнения теории упругости для плоского состояния получаются из соответствующих уравнений для объемной задачи путем
исключения из них производных по координате z . Уравнения равновесия (3.1.5) приобретают вид
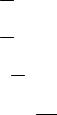
∂ σ |
x |
|
|
|
∂ τ |
|
|
|
||||
|
|
|
+ |
|
|
|
|
+ X = 0; |
||||
|
∂ |
x |
|
|
∂ |
y |
||||||
|
|
|
|
|
|
|
|
|||||
|
∂ τ |
|
|
|
∂ σ y |
|
|
|
||||
|
|
+ |
|
+Y = 0. |
|
|||||||
|
∂ |
x |
|
|
∂ |
y |
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения равновесия плоского сечения (статические граничные условия) (3.1.9) -
σxl +τ m = px ;
τ l +σ y m = py .
Система геометрических уравнений Коши (3.1.13) -
(3.1.25)
(3.1.27)
εx = |
∂ u |
; εy |
= |
∂ |
v |
|
γ xy = |
∂ |
u |
+ |
∂ |
v |
|
|
|
|
|
; |
|
|
|
|
; |
|
|||||
∂ x |
∂ |
y |
∂ |
y |
∂ |
x |
|
|||||||
|
|
|
|
|
|
|
|
|||||||
εz = γ yz = γ zx = 0. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
(3.1.28) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из шести условий совместности деформаций Сен-Венана остается только одно уравнение вида (3.1.16),
∂2ε |
x |
+ |
∂2ε |
y |
= |
∂2γ |
xy |
|
|
|
|
|
|
|
|
||||||
∂ y2 |
∂ x |
2 |
∂ x∂ |
y |
. |
|||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||
Наконец, закон Гука для изотропного материала, имеющий в прямой форме вид (2.7.7),
εx
εy
εz
в обратной записывается как
=E1 (σx − µσ
=E1 (σ y − µσ
=− µE (σx +σ
γxy = τGxy .
y );
);
x
y );
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σx = |
|
|
|
|
|
(εx + µεy ); |
|
|
|
|||||||||
|
|
|
|
2 |
) |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
(1 − µ |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
σ |
|
= |
|
|
E |
|
|
|
(ε |
|
+ µε |
|
); |
|
|
|
||
|
|
|
|
|
(1 − µ2 ) |
|
|
|
|
|
|||||||||||
|
|
|
|
y |
|
|
|
y |
|
|
x |
|
|
|
|
|
|||||
|
|
|
τ = Gγ xy = |
|
|
|
|
E |
|
|
|
|
|
|
|||||||
|
|
|
|
|
γ xy . |
|
|
|
|
||||||||||||
|
|
|
|
2(1 + µ) |
|
|
(3.1.29) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение сплошности (3.1.16) с учетом (2.7.7) может быть переписано в терминах напряжений, а именно |
|||||||||||||||||||||
|
∂ 2 |
|
(σx − µσ y ) |
+ |
∂ 2 |
(σ y − µσx )= 2(1 + µ) |
|
∂ 2τ |
|
||||||||||||
|
∂ y2 |
∂ x2 |
∂ |
x∂ y |
. (3.1.30) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Считая объемные силы X и |
Y постоянными, продифференцируем первое уравнение системы (3.1.25) |
||||||||||||||||||||
по x , а второе - по y , и сложим их почленно. Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
