
Основы проектирования машин / ГЛАВА 3
.4.pdf(3.4.38) в (3.4.36) приводит к однородной системе алгебраических уравнений относительно амплитуд |
Aj |
: |
||
r |
|
|
|
|
([a]p2 +[b]p +[c])A = 0 |
. |
|
(3.4.39) |
|
|
|
|
||
Далее, как обычно, для обеспечения существования нетривиального решения приравниваем нулю |
||||
определитель системы (3.4.39), что дает характеристическое уравнение |
|
|
|
|
det([a]p2 +[b]p +[c])= 0 |
. |
|
|
(3.4.40) |
|
|
|
||
Можно доказать, что если все элементы матрицы демпфирования (3.4.37) положительны, то вещественные части всех корней характеристического уравнения (3.4.40) отрицательны. Каждому вещественному отрицательному
корню p = −ω2 (в том числе и вещественной части комплексного корня) соответствует частное решение вида
q j |
= Aj exp(−ω2t) |
(3.4.41) |
|
. |
с вещественным значением Aj . Такие координаты со временем убывают, асимптотически приближаясь к нулевым значениям. Если все корни (3.4.40) вещественны и отрицательны, то система будет асимптотически приближаться
к положению равновесия, совершая монотонное затухающее движение неколебательного характера - апериодическое движение. Такое движение характерно для систем с сильным трением. Если среди корней
уравнения (3.4.40) находятся комплексно сопряженные вида p =α +iβ , p′ =α −iβ , α > 0 , то им отвечает затухающее колебательное движение
q j |
= exp(−α t)(B j cos βt +C j sin βt) |
(3.4.42) |
|
. |
Общее решение системы (3.4.36) является результатом линейного наложения частных решений (3.4.41) и (3.4.42).
Вынужденные колебания. Как указывалось выше, вынужденные колебания обуславливаются действием внешних возбуждений. Если система воспринимает действие внешнего возбуждения, то дифференциальные уравнения движения перестают быть однородными. В качестве внешнего возбуждения могут выступать силы, приложенные к сосредоточенным массам системы, или движения, возбуждающие некоторую часть системы. В любом случае, независимо от конкретной физической природы, возбуждение является явной функцией времени.
Рассмотрим движение линейной колебательной системы без затухания с s степенями свободы под |
|
|||||
действием внешних сил. Обозначим через Q1 , Q2 ,K, Qs |
обобщенные вынуждающие силы, соответствующие |
|||||
обобщенным координатам |
q1 , q2 ,K, qs |
Q j = Q j (t) |
j =1,2,K, s |
. Тогда в общем случае |
|
|
|
, причем |
, |
|
|
||
уравнения движения с учетом (3.4.11) будут выглядеть как |
|
|
|
|
||
|
|
s |
|
|
|
|
|
|
∑(a jk qk + c jk qk )= Q j |
|
|
||
|
|
&& |
|
, j =1,2,K, s , |
|
|
|
|
k =1 |
|
(3.4.43) |
||
а в прямой форме - |
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
a j q j + ∑c jk qk = Q j |
|
|
||
|
|
&& |
|
, j =1,2,K, s . |
|
|
|
|
k =1 |
|
(3.4.44) |
||
Решение систем (3.4.43) и (3.4.44) целиком определяется видом вынуждающей силы. Общим для любого решения является то обстоятельство, что вследствие неучтенного, но неизбежного сопротивления те колебания,
которые происходят с собственной частотой, постепенно затухают. По прошествии некоторого времени в системе будут присутствовать только движения, совершаемые с частотой вынуждающей силы - так называемые
установившиеся вынужденные колебания.
Гармонические вынуждающие силы. Предположим, что обобщенные вынуждающие силы изменяются по гармоническому закону
|
|
Q j |
= Fj sin(Ωt +ψ) |
j =1,2,K, s |
, |
(3.4.45) |
|
|
|
|
, |
|
|
||
т. е. имеют одинаковые частоты и начальные фазы, но различные амплитуды. Будем рассматривать |
|
||||||
установившееся движение. Тогда частное решение (3.4.43) с правой частью вида (3.4.45) имеет вид |
|
||||||
|
|
q j |
= Aj sin(Ωt +ψ) |
j =1,2,K, s |
. |
(3.4.46) |
|
|
|
|
, |
|
|
||
Подставляя (3.4.46) в дифференциальные уравнения (3.4.43), получим систему s алгебраических |
|
||||||
уравнений для определения амплитуд |
Aj |
: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∑s (−Ω2 a jk + c jk )Ak = Fj |
|
j =1,2,K, s , |
|
||
|
|
k =1 |
|
, |
(3.4.47) |
||
а подстановка в (3.4.44) дает |
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
−Ω2 a j Aj + ∑c jk Ak = Fj |
j =1,2,K, s . |
|
|||
|
|
|
k =1 |
, |
(3.4.48) |
||
Заметим, что точно такие же результаты получаются, если гармонический закон изменения обобщенных
сил и частных решений представлять в виде exp(iΩt), а не sin(Ωt +ψ).
Наиболее просто системы (3.4.47) - (3.4.48) решаются непосредственно алгебраическими методами, а именно: с помощью формул Крамера (если их определители отличны от нуля), методом Гаусса или любым другим известным в теории линейных алгебраических систем методом. Однако физически более наглядным является другой способ, заключающийся в разложении искомых амплитуд по собственным формам соответствующей однородной задачи. Приведем здесь без вывода частное решение системы (3.4.48), записанное в виде разложения по нормированным собственным формам:
|
|
q j |
= ∑ B2 |
i u ji |
2 sin(Ωt +ψ) |
|
|
|
|||
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
i=1 ω |
i |
−Ω |
, |
j =1,2,K, s |
, |
(3.4.49) |
||
|
|
|
|
|
|
|
|||||
|
s |
|
|
|
|
|
|
|
|
|
|
Bi |
= ∑Fk uki |
, i =1,2,K, s ; u ji - нормированные амплитуды i -ой собственной формы, |
|
||||||||
где |
k =1 |
|
|||||||||
j =1,2,K, s .
Выражение (3.4.49) позволяет сделать несколько выводов относительно характера колебаний в зависимости от соотношения между собственными частотами системы и частотой вынуждающей силы. Так, если
частота Ω вынуждающей силы совпадает с одной из собственных частот системы, например ωi , соответствующий член разложения (3.4.49) с течением времени неограниченно возрастает - наблюдается
явление резонанса. Частота возмущающей силы называется в этом случае критической. Возможен и
противоположный случай, когда при определенных значениях Ω достигается отсутствие колебаний, соответствующих выбранной координате, т. к. их амплитуды обращаются в нуль. Такое явление называется
антирезонансом. Если частота возмущающей силы близка к одной из собственных частот системы, то отвечающий ей член в разложении (3.4.49) значительно превышает все остальные. Конфигурация системы при этом почти совпадает с соответствующей собственной формой, а сами колебания почти точно воспроизводят форму одного из
собственных главных колебаний.
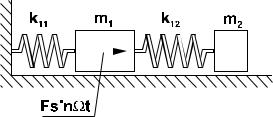
В качестве примера рассмотрим колебательную систему с двумя степенями свободы, на одну из масс которой действует гармоническая вынуждающая сила F sin Ωt (рис. 3.4.4). Как и ранее, за обобщенные
координаты примем отклонения грузов от положения равновесия, q1 = x1 , q2 = x2 . Дифференциальные уравнения движения рассматриваемой системы имеют вид
m1 x1 + (k11 + k12 )x1 − k12 x2 |
= F sin Ωt; |
|
|
||||
&& |
|
|
|
|
|
|
|
&& |
− k12 x1 + k12 x2 |
= 0. |
|
|
|||
m2 x2 |
|
. |
(3.4.50) |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.4.4
Подставляя в (3.4.50) частное решение (3.4.46), получаем следующую систему алгебраических уравнений для определения амплитуд A1 и A2 :
(k11 + k12 − m1Ω |
2 |
)A1 |
− |
k12 A2 = F; |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
(k12 − m2 Ω |
|
)A2 |
|
|
|
|
− k12 A1 |
|
|
|
|
+ |
2 |
= |
|
|
||||||
|
|
|
|
|
0. |
(3.4.51) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель D системы (3.4.51) равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D = |
|
(k |
|
+ k |
|
) − m Ω2 |
− k |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
|
|
11 |
|
|
|
12 |
1 |
|
12 |
2 |
|
|
|
||
|
|
|
|
|
|
|
− k12 |
k12 − m2 Ω |
. |
|
(3.4.52) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если определитель D из (3.4.52) отличен от нуля, решение (3.4.51) можно найти по формулам Крамера:
A1 |
= |
|
|
|
|
F(k12 |
− m2 Ω2 ) |
|
|
|
; |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(k11 |
+ k12 − m1Ω |
)(k12 |
− m2 |
Ω |
)− k12 |
|
|
||||||||
A2 = − |
|
|
|
|
|
Fk12 |
|
|
|
|
|
|
. |
|
|||
(k |
11 |
+ k |
12 |
− m |
Ω2 )(k |
12 |
− m |
Ω2 )− k 2 |
|
|
|||||||
|
|
|
|
|
1 |
|
|
2 |
|
12 |
|
|
(3.4.53) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из (3.4.53) следует, что резонанс в рассматриваемой системе наступает при условии |
|
|
|||||||||||||||
|
(k11 + k12 |
− m1Ω2 )(k12 − m2 Ω2 )− k122 |
= 0 , |
|
(3.4.54) |
||||||||||||
которое определяет два резонансных значения частоты возмущающей силы, равных собственным частотам ω1 и
ω2 системы. Антирезонанс наступает при условии
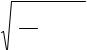
|
|
|
k |
12 |
− m |
2 |
Ω2 |
= 0 |
, |
(3.4.55) |
|||
|
|
|
|
|
|
|
|||||||
|
Ω 2 = |
k12 |
|
|
|
|
|
|
|
|
|
|
|
откуда частота антирезонанса |
m2 |
. При этой частоте колебания, соответствующие первой координате, |
|||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
A |
= |
F |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
k12 . |
||
полностью отсутствуют, а максимальное значение второй координаты согласно (3.4.53) равно |
|
||||||||||||
Полученный результат иллюстрирует принципиальную возможность подавления нежелательных колебаний. Рассмотренный пример можно трактовать следующим образом: введением в систему специально подобранной
дополнительной массы m2 , такой что |
m |
2 |
= k12 |
||
|
|
|
|
||
|
|
Ω , удалось устранить колебания основной части системы - |
|||
массы m1 .
Произвольные вынуждающие силы.
а) действие произвольной вынуждающей силы на линейную систему с одной степенью свободы.
Дифференциальное уравнение задачи о вынужденных колебаниях линейной системы с одной степенью свободы согласно (3.4.43) имеет вид
|
|
|
aq + cq = Q(t) , |
|
||||
|
&& |
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
&& |
2 |
q = |
Q(t) |
|
|
||
|
|
a , |
|
|||||
|
|
|
q +ω |
|
(3.4.56) |
|||
ω2 |
= |
c |
|
|
|
|
|
|
a - квадрат собственной частоты системы. |
|
|
|
|
|
|||
где |
|
|
|
|
|
|
||
Как известно из теории линейных дифференциальных уравнений, общее решение уравнения (3.4.56) есть
сумма общего решения соответствующего однородного уравнения (т. е. уравнения с нулевой правой частью) и некоторого частного решения уравнения (3.4.56). Общее решение однородного уравнения
|
|
|
q +ω |
2 |
q = 0 |
|
|
|
|
|
|
|
|
&& |
|
|
|
|
|
|
|
имеет вид |
|
|
q = Asin(ωt +ϕ), |
|
|
|
||||
|
|
|
|
|
(3.4.57) |
|||||
где постоянные амплитуда A и начальная фаза ϕ определяются из начальных условий. Если начальные |
|
|||||||||
условия таковы, что q(0) = q0 и |
q(0) = q0 |
, то |
|
|
|
|
|
|
|
|
|
& |
& |
|
|
|
|
|
|
|
|
|
|
|
q&0 |
|
2 |
2 |
|
ω q0 |
|
|
|
|
A = |
ω |
|
|
+ q0 |
ϕ = arctg |
|
|
|
|
|
|
& |
|
(3.4.58) |
|||||
|
|
|
|
|
|
|
; |
q0 . |
||
Частное решение (3.4.56) может быть получено классическим способом, а именно известным методом вариации произвольных постоянных. Но на практике этот метод не нашел большого применения. Дело в том, что аналитически задачу вынужденных колебаний системы удается решить только для чрезвычайно узкого круга систем с несколькими степенями свободы, а для численного решения гораздо удобнее другие методы, например, операционный [2, с. 272]. Суть этого метода заключается в следующем: зная решение уравнения (3.4.56) при какой-то одной известной правой части, можно отыскать его решение при любой другой правой части с помощью интегрирования. Применим этот метод к рассматриваемой задаче.
Пусть в некоторый момент времени t =τ к системе приложен мгновенный обобщенный импульс A0 , так
& |
A0 |
|
|
a . Тогда решение уравнения (3.4.56) при t >τ согласно (3.4.56) и (3.4.57) имеет |
|||
что q(τ) = 0; q(τ) = |
|||

вид
q = A R(t,τ), R(t,τ)= sin ω(t −τ) |
|
|
|
0 |
aω |
. |
(3.4.59) |
|
|||
Функция R(t,τ), описывающая движение, вызванное действием единичного импульса, называется
импульсной реакцией системы или функцией отклика.
Если теперь перейти к произвольной вынуждающей силе, рассматривая ее как бесконечную
последовательность элементарных импульсов, т. е. положив A0 = Q(τ)dτ , и просуммировать влияние всех этих импульсов, при нулевых начальных условиях получим
q = |
1 |
∫t |
q(τ)sin ω(t −τ)dτ |
|
aω |
|
|||
|
0 |
. |
(3.4.60) |
|
|
|
Интеграл типа (3.4.60) называется интегралом Дюамеля.
b) действие произвольной вынуждающей силы на линейную систему с s степенями свободы. Если действующие на многомассовую колебательную систему вынуждающие силы изменяются не по гармоническому
закону, то в общем случае решение задачи о движении такой системы удобнее всего проводить методом разложения по собственным формам колебаний.
Считаем, что предварительно найдены собственные частоты ωi |
и коэффициенты собственных форм λri . |
|||
Разложим вектор перемещений |
q |
r по собственным формам колебаний |
λri |
, представляя его в виде суммы |
|
|
|||
|
|
s |
|
|
|
|
qr = ∑λ riηi |
|
|
|
|
i=1 |
, |
(3.4.61) |
где ηi - нормальные координаты. Тогда система (3.4.44) после некоторых преобразований (подробнее с ними можно ознакомиться, например, в [29]; здесь приводится только окончательный результат) записывается в виде
&& |
2 |
|
|
j =1,2,K, s |
|
|
ηj +ω jηj = Q j |
, |
, |
(3.4.62) |
|||
|
|
|
|
|||
где Q j - приведенные вынуждающие силы, вычисляемые по формулам
s |
|
|
∑Qi λ ij |
|
|
Q = i=1 |
|
|
j s |
|
|
∑ai λ ij2 |
, j =1,2,K, s . |
|
i=1 |
(3.4.63) |
Поскольку каждое из независимых уравнений (3.4.62) описывает колебание некоторой системы с одной степенью свободы, то дальнейшее решение сводится к интегралу Дюамеля (3.4.60).
Рассмотрим в качестве примера хорошо знакомую систему на рис. 3.4.1a, положив, как раньше,
q1 = x1 , q2 = x2 ; k11 = k12 = k; m1 = m2 = m. Собственные частоты и собственные формы этой системы, как уже было найдено, определяются формулами (3.4.29) - (3.4.30). Пусть теперь на левый груз этой
системы действует вынуждающая сила вида

Q = F(1 −e−γt ) ,
где F и γ - известные константы. Приведенные вынуждающие силы согласно (3.4.63) равны
Q |
= |
Q |
|
|
|
= |
0,28F |
|
(1 −e−γt ); |
|
||||
|
|
2 |
|
|
|
|||||||||
1 |
|
m + m |
1,62 |
|
|
|
m |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
0,73F |
|
|
−γt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Q2 |
= |
|
|
|
|
|
= |
|
|
|
(1 −e |
|
). |
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
m + m 0,62 |
|
|
|
|
m |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
Уравнения движения (3.4.62) приобретают вид
&& |
+ 0,38 |
|
k |
η1 |
= |
0,28F |
|
|
−e |
−γt |
|
|
||||
|
|
|
|
|
(1 |
|
|
); |
||||||||
η1 |
m |
|
m |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
k |
|
|
|
|
0,73F |
|
|
|
|
|
|
||
η2 |
+ 2,62 |
|
|
η2 |
= |
|
|
(1 −e |
−γt |
|
||||||
|
|
|
|
|
|
|
|
|
). |
|||||||
&& |
|
|
m |
|
|
|
m |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решаем эти уравнения с помощью интеграла Дюамеля (3.4.60). Положив βi = ωγi , i =1,2 , получаем
η |
1 |
= |
0,28F |
|
1 |
− |
1 |
|
e−γt − |
|
β1 |
|
|
(sin ω |
|
t + β |
1 |
cosω |
t) ; |
|
|||||
|
|
2 |
|
|
2 |
|
|||||||||||||||||||
|
|
|
k |
|
|
|
|
|
1 + β |
1 |
|
|
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
1 + β 1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,22F |
|
|
|
1 |
|
|
|
β2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
2 |
= |
|
1 − |
|
e−γt − |
|
|
|
(sin ω |
2 |
t + β |
2 |
cosω |
2 |
t) . |
|||||||||
|
|
2 |
|
|
|
2 |
|
||||||||||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 + β 2 |
|
|
1 + β 2 |
|
|
|
|
|
|
|
|
|
|
|
||||
Наконец, законы движения xi = xi (t) , как следует из (3.4.61), записываются как
x1 =η1 |
+η2 ; |
|
x2 = λ |
|
|
21η1 + λ 22η2 . |
||
