
Основы проектирования машин / ГЛАВА 2
.9.pdf
ГЛАВА 2.9. УСТОЙЧИВОСТЬ МЕХАНИЧЕСКИХ КОНСТРУКЦИЙ
Под устойчивостью понимается свойство системы сохранять свое состояние при внешних воздействиях. Понятие устойчивости играет очень важную роль в механике. Дело в том, что если какая-либо механическая система сконструирована без учета требований устойчивости, то она будет чувствительна даже к самым незначительным внешним воздействиям, а это в конечном итоге может привести к самым нежелательным последствиям. Переход системы в неустойчивое состояние (или потеря устойчивости) также опасен, как и потеря ее прочности, т. е. способен вызвать полное разрушение данной конструкции. Вот почему так важно определить границы перехода механической системы от устойчивого состояния к неустойчивому.
a) |
b) |
c) |
|
Рис. 2.9.1 |
|
Определим состояние устойчивости как состояние, находясь в котором, механическая система при приложении любого сколь угодно малого внешнего воздействия (т. е. воздействия, которое является не только малым, но может быть сделано меньше любой наперед заданной величины) возвращается в исходное положение равновесия после снятия внешних силовых факторов. Значение внешней силы, при которой система переходит из
устойчивого состояния в неустойчивое, называется критической силой. Долю n внешней нагрузки по отношению к критической назовем запасом устойчивости.
Физический смысл устойчивости можно проиллюстрировать на простом примере (рис. 2.9.1). Если тяжелый шар находится внутри вогнутой поверхности (рис. 2.9.1a), то его состояние равновесия следует считать устойчивым, так как после малого толчка он будет двигаться со все уменьшающейся скоростью, причем чем слабее толчок, тем на меньшее расстояние произойдет отклонение от исходного положения. Если же шар находится в состоянии равновесия на вершине выпуклой поверхности (рис. 2.9.1b), то достаточно слегка толкнуть его, чтобы он начал с возрастающей скоростью удаляться от исходного положения равновесия – следовательно, исходное состояние равновесия неустойчиво. Когда же шар расположен на плоскости (рис. 2.9.1c), то с точки зрения устойчивости его равновесие безразлично.
Таким образом, устойчивым следует считать такое состояние механической системы, при котором любое внешнее отклонение от состояния равновесия вызывает реакцию системы, восстанавливающую это равновесие.
В качестве еще одного примера рассмотрим сжатие длинного стержня (или тонкостенной трубы)
центральной осевой нагрузкой F (рис. 2.9.2). При малых деформациях стержень остается прямым и после снятия нагрузки восстанавливает свое первоначальное положение. Возрастание осевой нагрузки приводит к резкому
увеличению деформаций изгиба. При больших значениях деформаций изгиба могут появиться признаки пластического деформирования, вследствие которых стержень не вернется в исходное состояние, а его ось останется криволинейной. Если такое явление имеет место, то говорят, что стержень потерял устойчивости. Следует отметить, что пластические деформации могут быть вызваны и деформациями растяжения, но в этом случае изогнутая ось стержня остается прямой. Отсутствие пластических деформаций при растяжении можно проверить по условию прочности, а при сжатии - по условию устойчивости.
Увеличение линейных размеров конструкции при постоянстве внешних силовых факторов также может привести к возникновению сильных пластических деформаций и даже к ее разрушению, несмотря на то, что все условия статической прочности будут выполнены.
Подобных примеров можно привести множество. Все они указывают на исключительную важность понятия устойчивости в механике.
Задача устойчивости сжатого стержня. Задачу расчета устойчивости проиллюстрируем на классическом примере: рассмотрим равновесие двухопорного стержня постоянного поперечного сечения A ,
нагруженного осевой силой F (задача Эйлера). После приложения осевой силы упругая линия стержня из линейной превращается в криволинейную (рис. 2.9.2). Если возникающий в сечении стержня изгибающий момент
M nx способен удержать стержень в изогнутом состоянии, то первоначальная прямолинейная форма равновесия стержня окажется неустойчивой. Форму упругой линии можно определить из уравнения изгиба стержня (2.5.22),
справедливого при малых прогибах:
EImin y′′ = −M nx . |
(2.9.1) |

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.9.2 |
|
|
|
||||
Здесь |
I |
min - минимальный осевой момент инерции (2.3.4), |
M nx |
= F y |
|||||||
|
|
|
- изгибающий момент. Знак “ - “ |
||||||||
в правой части уравнения обусловлен выбором направления кривизны (в данном случае кривизна уменьшается, поэтому вызывающая ее сила считается отрицательной). Записанное дифференциальное уравнение (2.9.1) можно представить в иной форме, а именно
y′′ + k 2 y = 0 |
, |
(2.9.2) |
||
|
|
|
||
где |
|
|
|
|
k 2 = |
F |
|
|
|
EImin . |
|
(2.9.3) |
||
|
|
|||
Общее решение такого уравнения, как известно, следует искать в виде |
|
|
||
y = C1 sin(kz) +C2 cos(kz) . |
(2.9.4) |
|||
Постоянные интегрирования в (2.9.4) выбираются так, чтобы были выполнены граничные условия:
y(z = 0)= 0 ; |
y(z = l)= 0 . |
Из первого условия однозначно следует C2 = 0 . Выполнение второго граничного условия приводит к
уравнению C1 sin(kl) = 0 , которое имеет два решения. Первое решение, C1 = 0 , соответствует варианту, при котором балка не деформируется, и практического интереса не представляет. Во втором случае, когда
sin(kl) = 0 , получаем kl = nπ , где n - произвольное целое число. Тогда для осевой нагрузки из (2.9.3) имеем
F = |
π 2 n2 EImin |
|
||
|
l 2 |
|
|
|
|
|
. |
(2.9.5) |
|
Наличие в выражении (2.9.5) целого множителя n означает, что при данной постановке задачи осевая |
||||
сила может принимать не любые значения, а только кратные n . Более того, меняя последовательно n |
и |
|||
определяя для каждого из них функцию y , можно обнаружить, что форма стержня при этом тоже меняется. Так, |
||||
при n =1 стержень принимает форму полуволны синусоиды, при n = |
2 на той же длине l укладывается уже |
|||
одна полная волна, и т. д. (рис. 2.9.3). В общем случае при любом целом |
n |
упругая линия балки описывается |
||
кривой
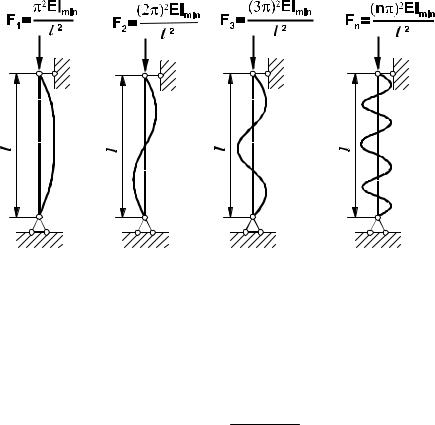
y =C1 sin |
πnz |
|
|
l , |
(2.9.6) |
которая представляет собой синусоиду, состоящую из n полуволн. Амплитуда C1 этой синусоиды равняется максимальному прогибу стержня, который в рамках принятых допущений (т.е. при рассмотрении только малых
прогибов, когда дифференциальное уравнение упругой линии стержня приближенно принимается линейным) определить нельзя.
Рис. 2.9.3
Дополнительные исследования показали, что переход от деформированного состояния с n =1 к состоянию с n = 2 всегда связан с большими деформациями при малом изменении нагрузки. Следовательно,
состояние при n =1 является предельным, а наименьшая отличная от нуля осевая сила Flim , соответствующая этому случаю, называется критической:
Flim = |
π 2 n2 EImin |
|
|
||
l |
2 |
. |
(2.9.7) |
||
|
|||||
Значение критической силы (2.9.7), определяющей границу устойчивости для случая сжатия стержня, впервые получено Эйлером, поэтому она получила название силы Эйлера.
Заметим, что, так же как и в рассмотренном выше простейшем примере, решение любой задачи устойчивости сводится к определению критической нагрузки и, следовательно, коэффициента запаса устойчивости. При решении задачи Эйлера этот результат получается путем решения дифференциального уравнения изгиба для соответствующих граничных условий. Однако на практике такая схема решения не является широко распространенной, поскольку часто приводит к громоздким вычислениям.
Энергетический метод определения критических нагрузок при расчете на устойчивость.
Среди других методов, используемых для решения задачи устойчивости, наиболее универсальным является
приближенный метод расчета критических нагрузок Flim , называемый энергетическим. Реализация этого метода может быть эффективной при использовании вычислительной техники.

Рис. 2.9.4
Рассмотрим стержень, к которому приложена постоянная сжимающая критическая сила Flim . Очевидно,
что после приложения этой нагрузки ось стержня изгибается (рис. 2.9.4). При этом критическая нагрузка Flim
совершает работу WF на осевом перемещении δ , величина которой,
WF = Flimδ , |
(2.9.8) |
по закону сохранения энергии должна быть численно равна увеличению потенциальной энергии деформации U , а |
|
именно |
|
U =WF . |
(2.9.9) |
C другой стороны, потенциальная энергия деформации при изгибе согласно (2.5.33) может быть подсчитана как сумма
|
1 |
|
|
k |
l |
M nx2 dz |
|
|
|||
U = |
|
|
|
|
∑i=1 |
∫0 |
|
|
|
||
2 |
EIi min |
, |
(2.9.10) |
||||||||
|
|
|
|
|
|
|
|
|
|
||
где k - число участков разного поперечного сечения; i и |
li |
- |
номер текущего участка равной площади и его |
||||||||
длина соответственно. Подставив в (2.9.10) выражение для M nx |
из (2.9.1), перепишем выражение (2.9.10) для |
||||||||||
потенциальной энергии в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
k |
l |
|
|
|
|
|
U = |
∑i=1 |
∫EIi min ( y′′)2 dz |
|
||||||||
2 |
(2.9.11) |
||||||||||
|
|
|
|
|
|
|
0 |
|
|
. |
|
Элемент длины dz после деформации повернется на угол dθ и сместится на величину dδ (рис. 2.9.4). |
|||||||||||
Тогда полное осевое перемещение точки приложения силы lF |
может быть подсчитано по формуле |
|
|||||||||
|
|
|
|
|
|
|
|
lF |
|
|
|
|
|
|
|
|
|
δ = ∫dδ |
|
|
|
||
|
|
|
|
|
|
|
|
0 |
, |
|
(2.9.12) |
Из геометрических соображений ясно, что
|
|
|
|
|
dδ = 2 sin2 |
dθ dz |
|
dδ = dz −dz cos(dθ) = |
2 |
. |
|||||
Поскольку в нашем случае углы поворота сечения деформированной балки считаются малыми, то |
|||||||
sin dθ |
= dθ |
= |
y′ |
|
|
|
|
|
|
|
|||||
2 |
|
2 |
2 , |
|
|
||
тогда |
|
|
|
|
|
|
|
|
1 |
l |
|
|
|
|
|
δ = |
∫F ( y′)2dz |
|
|
||||
|
2 |
0 |
. |
|
(2.9.13) |
||
|
|
|
|||||
Подставляя (2.9.8) и (2.9.11) в закон сохранения энергии (2.9.9) и разрешая его относительно критической силы, с учетом (2.9.13) получаем:
∑n ∫EImin ( y′′)2 dz
F = |
i=1 |
l |
|
|
|
i |
|
|
|
|
|
|
|
|
lim |
|
lF |
|
|
|
|
∫( y′)2 dz |
|
|
|
|
0 |
. |
(2.9.14) |
Из выражения (2.9.14) следует, что необходимым условием получения правильных решений является
наличие информации, описывающей поведение упругой линии стержня. Уравнение этой кривой y = y(z) приближенно может быть представлено в явной форме. К примеру, зададим его в виде степенного ряда с числом
членов на единицу большим количества граничных условий, которым необходимо удовлетворить:
y = a |
0 |
+ a z + a |
2 |
z 2 + a |
3 |
z3 |
+ a |
4 |
z 4 |
L+a |
n |
z n |
(2.9.15) |
|
1 |
|
|
|
+ |
|
. |
||||||
Постоянные множители a0 , a1 , a2 , a3 ,K, an |
ряда (2.9.15) определяются из граничных условий, |
|
|||||||||||
которые зависят от вида стержня, местоположения и типа опор типа, а также местоположения и вида внешних сил. При этом точность полученного результата, разумеется, напрямую зависит от точности описания формы изогнутой оси стержня.
Численные методы позволяют определить перемещение каждой точки стержня, что дает возможность использовать их для решения задачи устойчивости, не прибегая к процедуре аналитического описания изогнутой
оси y = y(z) . При таком подходе определение производных оказывается простой численной операцией, а задача расчета устойчивости существенно упрощается.
В том случае, когда на стержень действует несколько осевых сил, вызывающих его сжатие, работа этих сил имеет вид
|
|
1 |
m |
l j |
|
|
W∑F |
= |
∑Fj ∫( y′)2 dz |
|
|
||
2 |
|
|
||||
|
|
j=1 |
0 |
. |
(2.9.16) |
|
|
|
|
|
|||
где j - текущее значение осевой силы, m - общее число приложенных нагрузок; |
lj - расстояние от точки |
|||||
закрепления до точки приложения сжимающей силы. |
|
|
|
|
|
|
Критические напряжения. Если максимальную из приложенных сил назвать критической, а остальные выразить в долях по отношении к наибольшей, то подстановкой в уравнение сохранения энергии находится значение этой критической нагрузки. По значению критической нагрузки можно определить вызванное ею
критическое сжимающее напряжение σlim , т.е. то напряжение, при котором прямолинейная форма равновесия стержня становится неустойчивой:

σ |
lim |
= |
Flim |
|
|
|
|
|
|
|
|
A . |
|
(2.9.17) |
|||
|
|
|
|
|
||||
С целью выяснения границ применимости рассмотренной выше теории заметим, что выражение для |
||||||||
критической силы в случае произвольного стержня допустимо представить в виде |
|
|
||||||
Flim |
= |
π 2 EImin |
|
|
||||
|
(µ l)2 |
|
|
(2.9.18) |
||||
|
|
|
, |
|
||||
где µ - так называемый коэффициент приведения длины, зависящий от наложенных на стержень связей, |
||||||||
изменения жесткости сечения вдоль его оси и способа нагружения стержня. Коэффициент |
µ |
позволяет при |
||||||
расчетах и испытаниях на устойчивость заменять произвольный случай закрепления концов стержня основным случаем, т. е. стержнем с шарнирно закрепленными концами. Таким образом, результаты испытаний для основного
случая можно перенести на произвольный стержень, если для него известен коэффициент µ . Если стержень обладает постоянной жесткостью и нагружен сжимающей силой в концевых сечениях, величина µ
рассчитывается методом Эйлера. Значения µ для наиболее часто встречающихся вариантов закрепления приведены в таблице 2.9.1.
Таблица 2.9.1: Значения коэффициента приведения длины µ |
|
Способ закрепления концов стержня |
µ |
оба конца шарнирно закреплены |
1 |
оба конца заделаны |
0,5 |
один конец заделан, а другой шарнирно закреплен |
0,7 |
один конец заделан, а другой свободен |
2 |
Подставляя (2.9.18) в (2.9.17), получаем формулу
σlim = π(2 EI)min
µl 2 A
|
|
|
|
|
|
|
|
|
|
|
, |
|
которую удобнее записать как |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
σ |
lim |
= |
π 2 E |
|
|
||
|
|
|
|
|
λ2 |
, |
(2.9.19) |
|||||
|
|
|
|
|
|
|
|
|||||
λ = µ Imin |
/ imin |
- гибкость стержня; |
i |
min |
= I |
min |
/ A |
- наименьший радиус инерции поперечного |
|
|||
где |
|
|
|
|
|
|
||||||
сечения стержня.
Выражение (2.9.19) носит название формулы Эйлера для определения критических напряжений. Ею можно пользоваться только тогда, когда напряжения σlim в материале стержня, вызванные действием критической силы, не превышают предела пропорциональности σA (рис. 2.2.3),
σlim ≤σA , |
(2.9.20) |
поскольку в основу ее вывода было положено дифференциальное уравнение упругой линии стержня, справедливое лишь в пределах применимости закону Гука. С учетом (2.9.19) условие (2.9.20) приобретает вид

|
|
σ |
lim |
= |
π |
2 E |
≤ |
σ |
A , |
|
||
|
|
|
λ2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ ≥ |
|
π 2 E |
= λ |
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
σ A |
lim |
|
|
|
|
|
|
|
|
|
|
|
. |
(2.9.21) |
||
|
|
|
|
|
|
|
|
|
|
|
||
В правой части (2.9.21) стоит то наименьшее значение гибкости стержня, при котором формула Эйлера |
||||||||||||
λ |
lim |
= |
π 2 E |
|
|
|
|
|
|
|||
|
σA |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
еще применима, т. е. предельная гибкость |
|
|
|
, зависящая только от физико-механических |
|
|||||||
|
|
|
|
|
|
|
||||||
характеристик материала стержня - его модуля упругости и предела пропорциональности. Например, для дерева
λlim ≈110 , для чугуна - λlim ≈ 80 , для сталей - обычноλlim ≈100 . Однако для сталей с повышенным значением предела пропорциональности предельная гибкость уменьшается; так, некоторые легированные стали
обладают λlim ≈ 60 ÷70 .
Итак, при выполнении условия (2.9.21) расчет критических сил и напряжений можно проводить по
формулам Эйлера (2.9.18) - (2.9.19). Для стержней же с гибкостью меньше предельной, λ < λlim , действительные критические силы и напряжения значительно меньше тех значений, которые получаются из
(2.9.18) - (2.9.19). К примеру, при гибкости стального стержня, равной λ = 50 < λlim , в соответствии с (2.9.19)
имеем σlim ≈ 8 104 Н / см2 , что намного превышает не только предел пропорциональности, но даже пределы прочности и текучести большинства сталей. В таких случаях критические параметры можно определять по
эмпирическим формулам, одна из которых носит имя Ясинского:
σlim = a −bλ , |
(2.9.22) |
где a и b - некоторые определяемые экспериментально коэффициенты, зависящие от физико-химических свойств материала.
Формула Ясинского справедливая для пластичных материалов, т.е. материалов с гибкостью
λ′ < λ < λlim . На основании анализа многочисленных экспериментальных данных установлено, что для сталей
λ′ = 0,4λlim ; для цветных металлов - λ′ = 0,25λlim . При гибкости λ < λ′ напряжение σlim полагается
постоянным и равным пределу текучести σr .
Рис. 2.9.5 |
На рис. 2.9.5 приведен график критических напряжений, т. е. зависимость σlim =σlim (λ) . Из рисунка видно, что на участке λ < λ′ напряжение σlim имеет постоянное значение; участок λ′ < λ < λlim
описывается формулой Ясинского (2.9.22); при λ > λlim критическое напряжение определяется по формуле Эйлера (2.9.19).
В заключении следует отметить, что решение задачи устойчивости в общем виде и для любой твердотельной модели может быть выполнено методом конечных элементов.
