Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет — учебно-научно-производственный комплекс (бывш. ОрелГТУ)

Предмет:

Детали машин и основы конструирования

Файл:

Основы проектирования машин / ГЛАВА 2

.5.pdf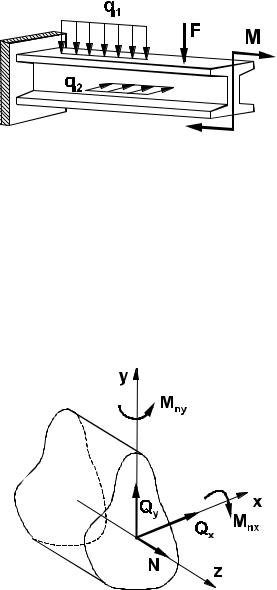

Скачиваний:

Добавлен:

01.05.2014

Размер:

318.14 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ГЛАВА 2.5. ИЗГИБ

Изгибом называется такой вид деформации, при котором под действием силовых факторов, вызывающих поперечное смещение оси бруса, наблюдается изменение кривизны его продольной оси. В результате продольные слои бруса нагружаются неравномерно: одни из них увеличивают первоначальную длину (удлиняются), в то время как другие - уменьшают (укорачиваются). На рис. 2.5.1 приведен пример одного из бесчисленного множества таких

нагружений. Здесь брус нагружается действующими в разных плоскостях распределенными силами q1 и q2 ,

поперечной сосредоточенной силой F и внешним моментом изгиба M .

Рис. 2.5.1

Внутренние силовые факторы. Вследствие изгиба в любом поперечном сечении бруса возникают напряжения, которые в общем случае представляют собой результат совместного действия поперечных

(касательных) Qx , Qy и нормальной N сил, а также моментов изгиба M nx и M ny (рис. 2.5.2). Как обычно, внутренние силовые факторы находятся методом сечений (см. главы 2.1 - 2.4). В соответствии с этим методом

абсолютные значения соответствующих проекций внутренних и внешних силовых факторов равны между собой.

Силы будем считать положительными, если они направлены вдоль координатных осей. Положительные направления моментов изгиба соответствуют правосторонней системе координат. Согласно этому, за положительное направление момента относительно оси принимаем такое его направление, при котором поворот системы координат выполняется против часовой стрелки, если наблюдать из конца вектора, определяющего положительное направление рассматриваемой оси.

Рис. 2.5.2

Сдвигающие нагрузки Qx и Qy вызывают напряжения, величинами которых на практике можно пренебречь по сравнению с напряжениями от других силовых факторов. Основными при таком нагружении, как

правило, являются напряжения, появляющиеся из-за действия моментов изгиба. Брус, у которого вследствие действия внешних нагрузок возникают в основном напряжения изгиба, как уже упоминалось во введении, называется балкой. Балками можно моделировать отдельные детали и элементы металлоконструкций. Плоскость, в которой лежит изогнутая ось балки, называется плоскостью изгиба, а плоскость действия силовых факторов - плоскостью нагружения. Если плоскости нагружения и изгиба совпадают, то имеет место плоский прямой изгиб (в противном случае изгиб считается неплоским).

а)

Рис. 2.5.3

Следует отметить, что механическая конструкция способна воспринимать внешнюю нагрузку, только если на нее наложены связи, выполненные в форме опор. Наличие опор при расчетах заменяется реакциями, которые зависят от вида этих опор. Как правило, встречаются следующие варианты закрепления балок: жесткая заделка (рис. 2.5.3a), неподвижная опора (рис. 2.5.3b), подвижная в осевом направлении опора (рис. 2.5.3c) и т. д. Жесткая заделка исключает любую подвижность, а число степеней свободы при этом становится равным нулю. Неподвижная опора ограничивает линейные перемещения, допуская угловые. Шарнирно-подвижная опора, кроме угловых, допускает также перемещения в направлении оси балки. Любое ограничение перемещения в плоском

случае нагружения вызывает либо реактивные силы Ra и Rr , либо реактивный момент M R , величины которых можно определить из уравнений статики. Если число неизвестных реакций превышает число статических

уравнений равновесия, т. е. балка статически неопределима, то следует добавить еще условие совместности деформаций.

Внешние силовые факторы, приложенные к балке, могут быть представлены в виде: сосредоточенных сил; сил, распределенных по длине или по площади; сосредоточенных либо распределенных моментов изгиба, а иногда и вращения.

В качестве примера рассмотрим один из простейших случаев нагружения: двухопорная балка длиной l ,

один конец которой неподвижен, а другой шарнирнозакреплен, нагружается сосредоточенной силой F (рис. 2.5.4a). Неизвестные внутренние силовые факторы, действующие в текущем сечении, определим методом

сечений. Для этого мысленно разрежем балку в месте расположения рассматриваемого сечения нормальной к оси плоскостью и рассмотрим равновесие одной из образовавшихся частей, заменяя действие другой внутренними силовыми факторами.

Построим графики зависимости внутренних силовых факторов от координаты расположения поперечного сечения (эпюры). Отметим, что эпюра моментов традиционно изображается со стороны сжатых слоев балки.

Рис. 2.5.4

Очевидно (рис. 2.5.4а), что нагружение балки представляет собой систему параллельных сил, для которой справедливы статические уравнения равновесия. Первое уравнение получается как результат суммирования

активных и реактивных сил (в общем случае их количество равно k ), а второе представляет собой уравнение моментов этих сил относительно одной из опор, например, опоры B :

∑k	Fi = 0 ∑k		M i = 0
i=1	;	i=1		,
или, в нашем случае,
RA + RB = F ;			RAl − Fb = 0 .		(2.5.1)
Решив систему (2.5.1), найдем реакции в опорах:
	RA =	Fb	RB =	Fa
	RA =	l ;	RB =	l .	(2.5.2)
		l ;		l .	(2.5.2)

Если за начало координат принять точку A , то момент изгиба в сечении балки, расположенном на расстоянии z , с учетом (2.5.2) имеет вид


Qy = RA =	Fb	M nx = RA z =				Fbz
Qy = RA =	l	M nx = RA z =			a +b ,		0 ≤ z < a ;
	l	,			a +b ,		0 ≤ z < a ;
		Qy = RA − F = −				Fa
		Qy = RA − F = −				l ,
						l ,
M nx = RA z − F(z −a) =			F(a2	+ ab −az)
M nx = RA z − F(z −a) =				a +b			, a ≤ z < a +b .
				a +b			, a ≤ z < a +b .

Результаты полученных зависимостей (2.5.3) и позволяют построить эпюры поперечных сил Qy (z)

моментов изгиба M nx (z)(рис. 2.5.4b-c).

(2.5.3)

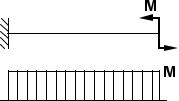
Рис. 2.5.5

Используем метод сечений для расчета внутренних силовых факторов в случае действия распределенной нагрузки q (рис. 2.5.5). Уравнения статики для выделенного элемента можно представить в виде

Qy −(Qy +dQy ) −qdz = 0
		,
M nx −(M nx + dM nx ) + qdz	dz	+(Qy + dQy )dz = 0
M nx −(M nx + dM nx ) + qdz		+(Qy + dQy )dz = 0
2		.	(2.5.4)

Если пренебречь в (2.5.4) величинами второго порядка малости, получим

dQy	= −q		dM	nx	= Qy
dz	= −q				= Qy
dz		, dz				.	(2.5.5)

С помощью дифференциальных уравнений (2.5.5) можно провести полный анализ изгиба балки (бруса).

Напряжения, вызванные изгибом. Задача расчета бруса, нагруженного моментами изгиба, в общем случае достаточно сложна, но решения сильно упрощаются, если использовать применительно к изгибу гипотезу плоских сечений. Предположим, что взаимное влияние слоев в поперечном направлении отсутствует, оси координат совпадают с направлением главных осей, а начало системы координат - с положением центра тяжести сечения. Согласно гипотезе плоских сечений поперечные сечения после деформации (параллельного смещения

сечения на расстояние δz и дальнейшего поворота в двух плоскостях на углы ϕx				и	ϕy относительно осей x и
y	соответственно) остаются плоскими, а перемещение	δxy	произвольной точки сечения с координатами			(x, y)
равно
	δxy	=δz	+ϕx y +ϕy x			(2.5.6)
			.			(2.5.6)

Если в поперечном сечении присутствует только изгибающий момент, то такой случай нагружения называется чистым изгибом (рис. 2.5.6). В частном случае плоского чистого изгиба из (2.5.6) имеем

Рис. 2.5.6

δxy =ϕx y	(2.5.7)
.

Рассмотрим этот случай более подробно. Выделим участок бруса площади A , на котором действует

только изгибающий момент M nx . Выделенный элемент после приложения внешнего момента деформируется (рис. 2.5.7). При этом внешние волокна бруса растягиваются, а нижние сжимаются, т. е. мы имеем дело с плоским

нагружением.

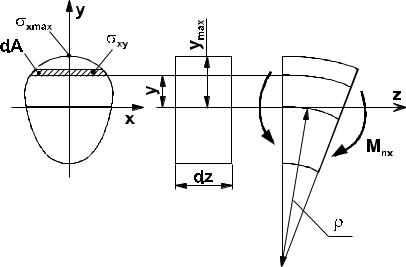
Рис. 2.5.7

Ось бруса, вдоль которой волокна не меняют длины после нагружения, называется нейтральной осью. Остается предположить, что положение нейтральных осей совпадает с направлением главных. Определить значение наибольших нормальных напряжений можно из уравнения равновесия отсеченной части. Для этого на

расстоянии y выделяем перпендикулярно оси бруса элемент площадью dA , на который будут действовать

только нормальные напряжения σ xy . Расстояние y представляет собой длину перпендикуляра, опущенного из текущей точки до рассматриваемой оси. Элементарный момент площадки относительно оси записывается в виде

			dM nx			=σxy ydA			(2.5.8)
								.	(2.5.8)
	Для того чтобы получить полный момент внутренних сил, необходимо просуммировать элементарные
моменты (2.5.8):
			M nx		= ∫dM nx
						A		.	(2.5.9)
	Если наибольшие нормальные напряжения σ x max			приложены на расстоянии					ymax , то согласно гипотезе
плоских сечений имеем
			σ xy	=		σ	x max
			y	=		ymax .			(2.5.10)
			y			ymax .			(2.5.10)
	Уравнение равновесия (2.5.9) с учетом (2.5.10) принимает вид
		M nx =			σx max			I x
		M nx =			ymax			I x
					ymax			,	(2.5.11)
Ix	= ∫y2dA
где	A	- осевой момент инерции ( 2.3.4) выделенного сечения.
	Если ввести в рассмотрение осевой момент сопротивления, равный

Wx =	1	∫y2dA

	ymax A		,	(2.5.12)

то из (2.5.11) получаем окончательное выражение для максимальных напряжений, возникающих под действием момента M nx :

σ	x max	=	M nx
	x max		Wx .	(2.5.13)
			Wx .	(2.5.13)

По аналогии с (2.5.9) - (2.5.10) можно записать выражение для наибольших напряжений при приложении момента M ny , а именно

σ y max =	M ny		Wy =		1	∫	x	2	dA
	Wy
				x
		;		x					.	(2.5.14)
		;			max A				.	(2.5.14)

В общем случае нагружения нормальное напряжение в текущей точке поперечного сечения определяется по формуле

σ		=	F	+	M	nx	y	+	M ny x
	z		z			nx
			A		I x				I y

										.	(2.5.15)
										.	(2.5.15)

В заключение заметим, что методы решения, основанные на гипотезе плоских сечений, дают удовлетворительные результаты для широкого круга инженерных приложений. Если же требуется проводить более точные расчеты, включая и расчеты местных напряжений, то следует использовать методы теории упругости (см далее главу 3.1 ).

Дифференциальное уравнение изогнутой оси бруса. В качестве примера рассмотрим брус, один

конец которого жестко закреплен, а к другому приложен момент изгиба M (рис. 2.5.6), что соответствует случаю чистого изгиба. Деформированное состояние бруса изображено на рис. 2.5.8. Если первоначальная длина

выделенного элемента dz , то растянутые слои, находящиеся на расстоянии y от нейтральной оси, получат

удлинение ∆dz . Величину напряжения, возникающего при этом удлинении, можно определить с помощью закона Гука (2.1.2):

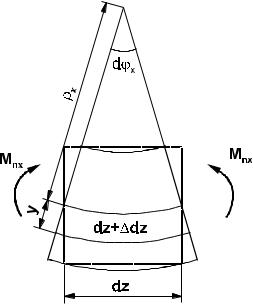
Рис. 2.5.8

		σ x		= E ∆dz
						dz ,			(2.5.16)
причем из рисунка видно, что
	dz = ρx dϕx ,					∆dz = ydϕx ,			(2.5.17)
где ρx - радиус кривизны оси. Подставляя (2.5.17) в (2.5.16) и учитывая (2.5.13), запишем выражение для
определения кривизны K x :
	K	x	=	1		=	M nx
		x		ρ	x		EI	x .	(2.5.18)
					x			x .	(2.5.18)
K y	имеем
Аналогично для	имеем

K	y	=	1	=	M ny
			ρy		EI y	.

С другой стороны, из дифференциальной геометрии известно, что кривизна линии K связана с поперечным перемещением u (прогибом) формулой

K =	1	=		u′′
	ρ		(1	+u′2 )3/2

				.

Для малых деформаций (а все полученные выше решения справедливы для случая упругого

деформирования, когда при малых перемещениях пластические деформации отсутствуют) величиной u′2 сравнению с единицей можно пренебречь, тогда

(2.5.19)

(2.5.20)

по

K =	1	= u′′
	ρ
		.	(2.5.21)

Подставляя (2.5.21) в (2.5.18) - (2.5.19), получим уравнение изогнутой оси бруса:

d 2ux

M nx

d 2uy

M ny

dz2

EI y

dz2

EI x

;

(2.5.22)

Радиус кривизны линейно связан с величиной угла поворота сечения ϕ . В общем случае углы поворота

сечений равны

∆ϕx =

∆z

∆ϕy =

M ny ∆z

EI y

EI x

;

(2.5.23)

Рассмотренные до сих пор варианты изгиба относились к случаю так называемого прямого изгиба, при котором внешний момент совпадал по направлению с одной из главных осей поперечного сечения. В случае, если это условие не выполняется, изгиб называется косым. При косом изгибе внешний момент необходимо представить в виде проекций на направление главных осей, а расчеты прочности следует выполнять так же, как и для случая прямого изгиба.

К задаче прямого изгиба можно свести и задачу расчета бруса, нагруженного внецентренной нагрузкой растяжения - сжатия. Внецентренным называется такой случай осевого нагружения, когда точка приложения осевой силы не совпадает с центром тяжести стыка. При этом осевую нагрузку можно перенести в центр тяжести сечения и, кроме осевой силы, добавить, по правилам механики, изгибающий момент. Далее следует разложить момент на составляющие относительно главных осей, что и сводит задачу внецентренного нагружения к расчету прямого изгиба.

Касательные напряжения от поперечных сил. Проведенное выше рассмотрение проводилось в предположении, что в поперечных сечениях бруса возникают только нормальные напряжения, что совершенно справедливо при чистом изгибе. Однако в отдельных случаях, в частности, при поперечном изгибе, пренебрежение поперечной нагрузкой может привести к существенным погрешностям, что вынуждает учитывать и касательные напряжения.

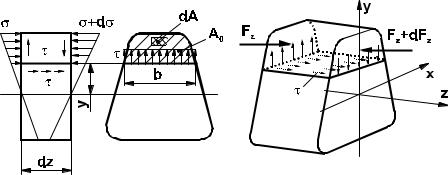
Рассмотрим брус при поперечном изгибе. Выделим элемент объема толщиной dz , текущей шириной b и

приложим к нему сдвигающую силу Qy (рис. 2.5.9). Очевидно, что по закону парности касательных напряжений величины напряжений сдвига в поперечном и продольных сечениях равны. Для расчета нормальных σ и касательных τ напряжений мысленно разделим этот элемент на две части продольным сечением,

расположенным на расстоянии y от нейтрального слоя, и рассмотрим равновесие одной из отсеченных частей площадью A0 . Равнодействующая Fz нормальных сил в левом сечении выделенной части элемента равна

Рис. 2.5.9

= ∫∫σ dA

или, учитывая, что согласно (2.5.15) можно записать

σ =

yM nx

I x

получаем

M nx

∫∫ydA =

M nx Sz0

I x

(2.5.24)

где y

Sz0 = ∫∫ydA

- текущая ордината площадки dA , а выражение

представляет собой статический момент

площади поперечного сечения отсеченной части фигуры относительно нейтральной оси.

Аналогично для равнодействующей нормальных сил в левом сечении имеем

Fz + dFz = ∫∫(σ + dσ)dA =

(M nx + dM nx )Sz0

I x

(2.5.25)

Разность этих сил уравновешивается касательными силами, возникающими в продольном сечении

выделенного элемента. Если предположить, что касательные напряжения распределены по ширине b сечения равномерно, то

dM nx Sz0

=τ bdz

I x

(2.5.26)

откуда с учетом (2.5.5) окончательно получаем так называемую формулу Журавского:

τ =

Qy Sz0

I xb .

(2.5.28)

Используем соотношение (2.5.28) для расчета распределения касательных напряжений по высоте бруса

прямоугольного поперечного сечения площадью A = bh , нагруженного действующей вдоль оси

y поперечной

силой

(рис. 2.5.10). Для точек, имеющих текущие ординаты

, имеем

Sz0 =

− y2

= bh

;

12 .

(2.5.29)

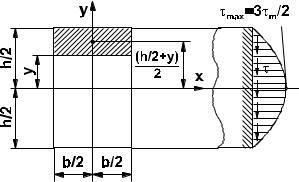
Рис. 2.5.10

После подстановки (2.5.29) в (2.5.28) находим

	6Qy h2				2
τ =				− y

	bh	3	4
	bh		4			.	(2.5.30)
						.	(2.5.30)

Из (2.5.30) видно, что наибольшие касательные напряжения имеют место на нейтральной линии (при y = 0 ),

τ	max	=	3Qy	=	3	τ	m ,
			2A		2			(2.5.31)

τ		=	Qy
	m		A - среднее значение касательного напряжения.
где

Формула Журавского применима также для определения касательных напряжений в тонкостенных брусьях незамкнутого профиля (тонкостенным будем считать сечение, у которого отношение его толщины к периметру

удовлетворяет неравенствуδ / l ≥10 ). Для случая тонкостенного открытого контура касательные напряжения направлены по касательной к средней линии контура. Можно считать, что по толщине контура они не меняются. В

остальном методы расчета касательных напряжений не отличаются от методов, описанных выше. В качестве примера рассмотрим тонкостенный незамкнутый профиль, который изгибается относительно оси x под действием

вертикальной поперечной силы Qy , параллельной оси y . Картина распределения касательных напряжений по

длине тонкостенного незамкнутого сечения, рассчитанная с помощью (2.5.28), показана на рис. 2.5.11. Видно, что
τmax	=	(4b + h)hQy

		8I x	, имеют место в местах, расположенных на нейтральной
наибольшие напряжения, равные

оси в непосредственной близости к центру тяжести.

1 / 21 2 > Следующая >>>

Соседние файлы в папке Основы проектирования машин

#
01.05.2014298.62 Кб65ГЛАВА 2.11.pdf
#
01.05.2014173.73 Кб62ГЛАВА 2.12.pdf
#
01.05.2014271.23 Кб62ГЛАВА 2.2.pdf
#
01.05.2014191.23 Кб61ГЛАВА 2.3.pdf
#
01.05.2014461.33 Кб62ГЛАВА 2.4.pdf
#
01.05.2014318.14 Кб62ГЛАВА 2.5.pdf
#
01.05.2014338.57 Кб62ГЛАВА 2.6.pdf
#
01.05.2014304.13 Кб68ГЛАВА 2.7. НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ.pdf
#
01.05.2014282.97 Кб66ГЛАВА 2.8.pdf
#
01.05.2014297.19 Кб61ГЛАВА 2.9.pdf
#
01.05.2014250.52 Кб66ГЛАВА 3.1. ОБЩИЙ СЛУЧАЙ РАСЧЕТА НАПРЯЖЕННО - ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ.pdf