
Основы проектирования машин / ГЛАВА 2
.2.pdf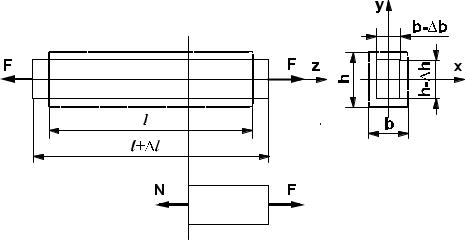
ГЛАВА 2.2. РАСТЯЖЕНИЕ (СЖАТИЕ) СТЕРЖНЕВЫХ МОДЕЛЕЙ |
Простейшим случаем силового воздействия является центральное нагружение стержня внешней |
нагрузкой, вызывающей его растяжение или сжатие (под центральным понимается такое нагружение, при |
котором точка приложения силы совпадает с центром тяжести сечения). В дальнейшем растяжению предписываем |
знак плюс (+), а сжатию - минус (-). Такое нагружение приводит либо к удлинению стержня (в случае растяжения), |
либо к его укорочению (в случае сжатия). Растяжение (сжатие) прямых стержней - достаточно простой вид |
напряженного состояния, который легко реализовать при лабораторных испытаниях. Поэтому этот тип |
напряженного состояния является базовым, к которому можно привести и другие варианты напряженных |
состояний. В этой связи на нем следует остановиться более подробно. |
Рис. 2.2.1 |
Деформации. Рассмотрим однородный стержень прямоугольного поперечного сечения площадью A |
= bh и длиной l , к торцам которого приложены внешние растягивающие силы F (рис. 2.2.1). |
Воспользовавшись методом сечений, легко установить, что во всех поперечных сечениях стержня возникнут |
одинаковые нормальные внутренние силы N , равные по абсолютной величине силе F , N = F . Сила N |
является равнодействующей элементарных внутренних нормальных сил σ dA, распределенных по площади |
поперечного сечения A . Закон распределения нормальных напряжений σ по сечению устанавливается с |
помощью гипотезы плоских сечений: плоские поперечные сечения стержня при упругом растяжении (сжатии) |
смещаются параллельно исходным положениям, оставаясь при этом плоскими. Поскольку согласно гипотезе |
плоских сечений в однородном стержне внутренние силы распределены по любому сечению равномерно, то |
нормальные напряжения растяжения σ во всех точках текущего сечения должны быть одинаковыми и равными |
σ = N / A . |
Нормальное нагружение приводит к осевому удлинению стержня на величину ∆l . Отношение абсолютного |
продольного удлинения ∆l стержня к его первоначальной длине l называется относительной продольной |
деформацией, или относительным продольным удлинением εz : |
ε |
z |
= ∆l |
|
|
l . |
(2.2.1) |
|
|
|
Удлинение стержня приводит также к уменьшению его поперечных размеров, что, в свою очередь характеризуется относительными поперечными деформациями εx и εy :

ε |
x |
= − ∆b |
ε |
y |
= − ∆h |
|
|
b ; |
|
h . |
(2.2.2) |
||
|
|
|
|
|||
|
|
|
|
|
εx = εy |
. |
Отметим, что для изотропных материалов справедливо равенство |
||||||
Закон Гука. Один из фундаментальных законов механики - |
закон Гука, устанавливающий линейную |
|||||
зависимость между нормальным напряжением σ |
и относительным удлинением ε |
- для центрального |
||||
растяжения (сжатия) формулируется в виде |
|
|
|
|
|
|
|
|
|
σ = Eε , |
(2.2.3) |
||
где E - коэффициент пропорциональности, который называется модулем упругости, или модулем Юнга, а фактическая его величина зависит от механических свойств материала.
Важной характеристикой прочности материала является также коэффициент Пуассона µ . Величина этого коэффициента определяется абсолютным значением отношения поперечной деформации к продольной,
|
µ = abs( |
εx ) = abs( |
εy |
) |
|
|||||
|
|
|
||||||||
|
|
|
εz |
|
|
|
εz , |
(2.2.4) |
||
где abs(x) - абсолютное значение числа x . Численное значение µ для большинства металлов лежит в |
|
|||||||||
пределах 0,25 ≤ µ ≤ 0,3 . |
|
|
|
|
|
|
|
|
|
|
Закон Гука можно записать в другой форме. Из (2.2.3) и (2.2.4) следует, что |
|
|||||||||
ε |
z |
= σ z |
ε |
x |
= ε |
y |
= −µσ z |
|
||
|
E , |
|
|
|
|
E . |
(2.2.5) |
|||
|
|
|
|
|
|
|
|
|||
Очевидно, что растяжение в направлении приложения нормальной силы вызывает удлинение в этом направлении и сжатие в перпендикулярном. Вот почему для случая нормального нагружения в трех взаимно перпендикулярных плоскостях соотношения для расчета относительных удлинений с учетом (2.2.3) принимают вид
εx = σEx − µ(σEy + σEz ) ,
εy = |
σ y |
− µ( |
σ |
x + |
σ |
z ) |
|
E |
|
|
|
||||
|
|
E |
E , |
(2.2.6) |
|||
εz = σEz − µ(σEx + σEy ) .
Выражение (2.2.6) получило название обобщенного закона Гука.
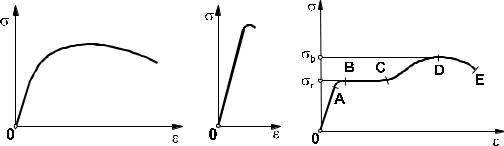
Рис. 2.2.3 |
Рис. 2.2.4 |
Рис. 2.2.2 |
Линейная зависимость, определенная законом Гука, справедлива только для области упругих деформаций и нарушается при появлении признаков пластического деформирования (напомним, что под пластическим деформированием понимается такой случай нагружения, при котором деформированное состояние тела не возвращается в исходное после снятия внешней нагрузки). Для того чтобы разобраться в характере разрушения и найти количественные характеристики прочности материала, его испытывают на растяжение (сжатие). На рис. 2.2.2 изображена типичная кривая, полученная при испытании на растяжение образцов из низколегированных сталей.
Здесь на участке OA сохраняется прямая пропорциональная зависимость, а координаты точки A определяют
предел пропорциональности. Участок BC характеризуется появлением пластических деформаций, которые растут даже без приложения нагрузки. Это явление называют текучестью материала, а напряжение,
соответствующее точке C , - пределом текучести σr . На участке CD напряжение возрастает и в точке D достигает максимального значения. Дальнейшее удлинение приводит к разрушению материала. Напряжение,
соответствующее точке D , носит название предела прочностиσb . Для материалов из высоколегированной стали нет явно выраженной площадки текучести, а потому используется понятие условного предела текучести
(рис. 2.2.3), за который принимают напряжения, при которых остаточная деформация равна ε = 0,002 . Для хрупких материалов явление текучести вообще не имеет место, а кривая растяжения имеет вид, показанный на
рис. 2.2.4.
Допускаемые напряжения и условие прочности. Очевидно, что, имея результаты испытаний материала на растяжение (сжатие), можно определить границы возможного нагружения, или, как их называют на
практике, допускаемые напряжения по текучести σar и прочности σab , величины которых рассчитываются по формулам
σ |
ar |
= σr |
σ |
ab |
= σb |
|
|
nr |
|
nb , |
|
||
|
|
, |
|
(2.2.7) |
где nr , nb - коэффициенты запаса статической прочности (подробнее о коэффициентах запаса см. в главе 2.7 ).
Одним из важнейшим критерием расчета любой механической конструкции является условие прочности. Оно считается выполненным, если фактически действующее напряжение не превышает допускаемое. Поэтому условие прочности имеет вид:
• |
по пределу текучести - |
σ ≤σar ; |
|
• |
по пределу прочности - |
σ ≤σab . |
(2.2.8) |
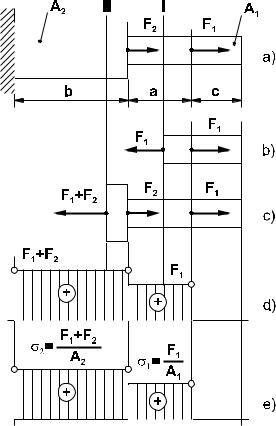
Рис. 2.2.5 |
Распределение нормальных напряжений и осевых сил. Растяжение (сжатие) характеризуется величинами нормальных напряжений, возникающих от действия внешних нагрузок. Поскольку напряжения меняются по длине стержня, то для того чтобы иметь полную информацию об его напряженном состоянии, необходимо построить график распределения нормальных напряжений по длине. Такой график называется эпюрой. Для построения эпюр напряжений растяжения и растягивающих сил можно воспользоваться методом сечений ( глава 2.1 ). На рис. 2.2.5a изображен жестко закрепленный одним концом стержень, состоящий из двух участков с
различными поперечными сечениями, который нагружен парой центральных сил F1 и F2 . Площади поперечных
сечений обозначим через A1 и A2 . Как уже упоминалось выше, для нахождения внутренних усилий в некотором текущем сечении необходимо мысленно разрезать брус в этом сечении и рассмотреть равновесие отсеченной
части. Проделав эту процедуру дважды - для сечений I и II (рис. 2.2.5b,c) - легко построить эпюры усилия растяжения (рис. 2.2.5d) и нормального напряжения (рис. 2.2.5e).
Напряжения в наклонных сечениях. Испытания на растяжение (сжатие) помогают также сделать вывод относительно характера процесса разрушения. Для этого рассмотрим напряжения, возникающие на
наклоненной под углом α к оси площадке бруса, растянутого продольной силой F (рис. 2.2.6). Равнодействующая внутренних сил в этом наклонном сечении направлена вдоль оси стержня и равна внешней
растягивающей силе F . Представим эту равнодействующую в виде суммы проекций Nα и Qα на два взаимно-перпендикулярных направления (в плоскости сечения и перпендикулярно к нему),

Рис. 2.2.6
Nα = F cosα , Qα = F sinα .
Если площадь поперечного сечения бруса обозначить через A , то площадь наклонной площадки равна
Aα = A/ cosα , а напряжения на этой площадке -
σα = |
Nα |
= |
|
F |
cos2 α =σ cos2 |
α |
|||
Aα |
|
||||||||
|
|
|
A |
|
|
|
, |
||
|
|
|
|
|
|
|
|
|
|
|
τα |
= |
Qα |
= |
1 |
σ sin 2α |
|
||
|
Aα |
2 |
|
||||||
|
|
|
|
, |
(2.2.9) |
||||
|
|
|
|
|
|
|
|
||
где σ = F / A . Напряжения σα и τα являются соответственно нормальными и касательными напряжениями в наклонном сечении.
Нормальные напряжения σα , действующие на наклонной площадке, согласно (2.2.9) достигают
максимальной величины при α = 0 , причем σmax =σ . Заметим, что при этом значении угла касательные напряжения отсутствуют. Площадки, на которых действуют только нормальные напряжения, называются
главными площадками, а сами эти напряжения - главными напряжениями. Таким образом, расчет прочности стержней в условиях упругого растяжения следует проводить по нормальным напряжениям в поперечных сечениях.
Вызывающие относительный сдвиг слоев материала касательные напряжения τα , как следует из (2.2.9),
максимальны при α =π / 4 и α = 3π / 4 , τmax =σ / 2 . При этом нормальные напряжения в этих сечениях по величине равны касательным.
Эксперименты показали, что поверхности разрушенных при растяжении (сжатии) стержней, как правило,
наклонены под углом α =π / 4 , поэтому именно наибольшие касательные напряжения можно с уверенностью

назвать главной причиной разрушения материалов.
При α =π / 2 (т. е. на продольных площадках) отсутствуют как нормальные, так и касательные напряжения. Это означает, что продольные слои стержня не взаимодействуют между собой.
Решение статически неопределимых задач при растяжении (сжатии). Рассмотренные выше методы определения внутренних силовых факторов далеко не всегда оказываются достаточными для решения всего многообразия задач растяжения (сжатия) механических стержневых конструкций. В инженерной практике часто встречаются так называемые статически неопределимые системы, у которых имеется большое число наложенных связей. В этом случае для определения внутренних силовых факторов (реакций) одних уравнений статического равновесия оказывается недостаточно. Разность между числом реакций и числом возможных независимых уравнений равновесия называется степенью статической неопределимости. Найти все неизвестные силы (или, как говорят, раскрыть статическую неопределимость) можно, дополнив систему уравнений статики - например, условиями совместности деформаций (подробнее о методах решения статически неопределимых задач будет сказано в главе 2.6 ).
Рис. 2.2.7
Рассмотрим принцип составления уравнений совместности деформаций на простом примере нагружения стержня, аналогичного изображенному на рис. 2.2.5a, только жестко заделанного с обеих сторон (рис. 2.2.7a). Для
решения задачи устраним внешние опоры, заменив их действие силами реакции X1 и X 2 , и рассмотрим равновесие стержня (рис. 2.2.7b). Ясно, что данная система однократно статически неопределима, поскольку две
реакции опор не могут быть найдены из одного уравнения статического равновесия:
F1 + F2 − X1 − X2 = 0 .
Уравнение совместности деформаций должно выражать тот очевидный факт, что в условиях жесткого закрепления общее удлинение стержня, т. е. смещение одного из торцов относительно другого, равно нулю:
F2b |
+ |
F1a |
+ |
F1b |
− |
X1 (a + c) |
− |
X1b |
= 0 |
|
EA |
EA |
EA |
EA |
EA |
||||||
2 |
|
|
|
. |
||||||
|
|
1 |
|
2 |
|
1 |
|
2 |
Решая систему полученных уравнений, имеем
X1 |
|
(F1 |
+ F2 )b |
|
F1a |
|
|
(a + c) |
|
b |
|
|
|
|
|
|
= |
+ |
|
/ |
+ |
|
|
|
|
|
|
||||||
|
|
A1 |
|
|
|
X |
|
= F + F − X |
|
|||||||
|
|
|
A2 |
|
A1 |
A2 |
; |
2 |
1 . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|||
Другой пример статически неопределимой стержневой системы из трех стержней одинаковых сечений,
нагруженных вертикальной силой F , приведен на рис. 2.2.8. Уравнения равновесия в этом случае имеют вид

|
|
Рис. 2.2.8 |
|
|
|
|
|
|
X 2 |
= X 3 |
; |
F − X |
1 |
− 2 X |
2 |
cosβ = 0 |
. |
|
|
|
|
|
||||
Для того чтобы записать условие совместности перемещений, нужно рассмотреть деформированное состояние данной стержневой системы, которое характеризуется смещением узловой точки на некоторую величину
δ1 = OO′ . Будем считать, что деформации малы, т. е. угол OO′B2 = OO′B3 = β . Очевидно, что при этом перемещения боковых стержней связаны с перемещением центрального выражением
δ2 = δ3 = B2O′ = B3O′ = δ1 cos β
или
|
|
|
|
|
|
|
|
|
|
|
X2 l |
|
= |
X1l |
cosβ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
EAcos β |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
EA |
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение этих уравнений дает |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
X2 = |
|
|
|
|
F cos2 β |
|
|
X1 = |
|
|
F |
|
|
|||||||
|
|
|
|
|
1 −2 cos3 β |
; |
1 |
−2 cos3 β |
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
b) |
|
Рис. 2.2.9 |
Потенциальная энергия деформации. Рассмотрим стержень длиной l с постоянным поперечным сечением A , испытывающий чисто осевое нагружение силой F (рис. 2.2.9a). Внешняя сила совершает работу
WF , величина которой численно равна потенциальной энергии U , накопленной стержнем. Работа внешней силы, в свою очередь, равняется площади под кривой, описывающей зависимость деформации от нагрузки. Поскольку
такая зависимость при отсутствии пластических деформаций, как следует из закона Гука, линейна (рис. 2.2.9b), то
для работы текущей силы |
Fm |
на элементарном перемещении |
d(∆l) |
стержня имеем |
|
|
|
||||
|
|
dWF = Fm d(∆l). |
(2.2.10) |
||
Суммарная работа внешней силы F на упругом перемещении ∆l ( ∆l |
- абсолютное удлинение стержня), |
||||
вообще говоря, определяется интегрированием (2.2.10) по всем элементарным участкам, но в данном случае вследствие прямой пропорциональности между силой и перемещением численно равна площади треугольника
OM1M :
WF =U = |
1 |
F∆l |
|
2 |
|
||
|
. |
(2.2.11) |
Отметим, что в дальнейшем при вычислении работы внешней силы в условиях упругого нагружения
коэффициент 1/ 2 будем ставить без подробных объяснений. Подставляя в (2.2.11) выражение для ∆l из закона Гука (2.2.3), с учетом (2.2.1) получаем
|
U = |
F 2l |
|
|
|
|||
|
2EA . |
(2.2.12) |
||||||
|
|
|
||||||
Если внутренняя сила N меняется вдоль стержня, то потенциальная энергия деформации равна |
||||||||
U = ∫l |
dU |
dU = |
N 2 dz |
|
||||
2EA . |
||||||||
0 |
|
; |
|
|
|
|||
Конечный результат интегрирования зависит от конкретного вида зависимости N = N(z). |
||||||||
|
F |
Fy |
и |
F |
действуют в трех |
|||
Вариант нагружения, при котором нормальные силы |
x , |
|
z |
|||||
взаимно-перпендикулярных направлениях, называется трехосным растяжением (сжатием). Рассмотрим элемент объема в виде параллелепипеда dV = dxdydz , по граням которого действуют нормальные напряжения σ x ,
σ y , σ z (рис. 2.2.10). Для того чтобы определить энергию деформации, накопленную параллелепипедом,
воспользуемся выражением (2.2.10). Если перемещения граней обозначить как ∆dx, ∆dy и ∆dz , то энергия dU элементарного объема может быть рассчитана по формуле
dU = |
1 |
(F ∆dx + F |
∆dy + F ∆dz) |
|
|
||||
|
2 |
x |
y |
z |
|
|
|
, |
|
или

dU = |
1 |
(σxεx +σ yεy +σzεz )dxdydz |
|
|||||||||
2 |
|
|||||||||||
|
|
|
. |
(2.2.13) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.2.10
Подстановка в (2.2.13) выражений для |
εx ,εy |
и |
ε |
z из (2.2.6) окончательно дает |
|||
|
|
||||||
dU = |
1 |
[σx |
2 +σ y |
2 +σz |
2 |
−2µ(σxσ y +σxσz +σ yσz )]dxdydz |
|
2E |
|
||||||
|
|
|
|
|
|
. (2.2.14) |
|
