
Основы проектирования машин / ГЛАВА 2
.6.pdfГЛАВА 2.6. МЕТОДЫ РАСЧЕТА ДЕФОРМИРОВАННОГО СОСТОЯНИЯ УПРУГИХ СИСТЕМ
Действующая на тело внешняя нагрузка, как известно, приводит к его деформированию и последующему появлению внутренних напряжений (глава 2.1 ). Величины перемещений точек тела, вызванных действием внешних сил, определяют деформированное состояние механической системы, которое в свою очередь может существенно влиять на ее работоспособность.
Кроме перемещений, в практике проектирования используют понятие жесткости. Жесткость как физическое понятие представляет собой способность тела сопротивляться внешнему деформированию и численно равна нагрузке, которая вызывает единичное перемещение. Величина, обратная жесткости называется податливостью. Податливость характеризует способность тела перемещаться (деформироваться) под действием внешнего силового воздействия. Единицей измерения податливости служит перемещение точки тела под действием единичной силы.
Очевидно, что расчет жесткости напрямую связан с определением перемещений рассматриваемых точек детали. При этом следует различать природу возникновения деформаций. Если при нагружении детали деформация распределена по всему объему, то ее можно считать объемной. Имеют место также деформации контактные, которые в отличие от объемных локализованы внутри малых по сравнению с размерами тела объемах и быстро затухают. Необходимо однако отметить, что такое деление деформаций на объемные и контактные является условным.
Внемногочисленных частных случаях объемные и контактные деформации можно рассчитать аналитическими методами. Но для решения задачи расчета полей перемещений в деталях произвольной геометрической формы используются исключительно численные методы. Для реализации численных методов разработаны компьютерные программы, которые позволяют получить полную картину деформированного состояния детали.
Вэтой главе рассмотрены некоторые из аналитических приемов расчета перемещений, каждый из которых можно эффективно применять при решении ряда конкретных задач. Численные методы будут изложены ниже в главе 3.3 .
Определение перемещений методом интегрирования уравнения изогнутой оси балки.
После приложения к телу внешней нагрузки его точки перемещаются. Обычно величины упругих перемещений считаются малыми по сравнению с геометрическими размерами деформируемых тел. Это условие положено в основу дальнейших расчетов.
Рассмотрим эти перемещения на примере консольной балки длиной l с односторонней внешней заделкой (рис. 2.6.1). К свободному концу балки приложена сосредоточенная сила F , которая и вызывает деформации ее
точек. Прогиб балки в текущем сечении обозначим как δ . Выделим элемент объема балки длиной dz , находящийся на расстоянии z от закрепленного конца. Деформированное состояние в текущем сечении балки
|
Kz = |
1 |
|
|
ρ |
ρ |
z ) ее изогнутой оси. Согласно (2.5.18) искомую |
||
описывается радиусом кривизны z (или кривизной |
|
|
||
кривизну можно определить как |
|
|
|
|
K |
z |
= |
1 |
= |
M nx |
|
|
||
|
|
ρ |
z |
|
EI |
x , |
(2.6.1) |
||
|
|
|
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
M nx = F(l − z). |
(2.6.2) |
||||||||
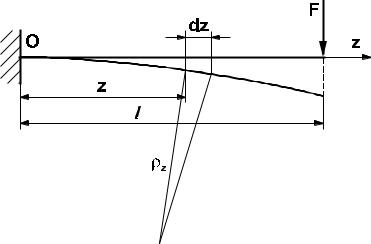
Рис. 2.6.1
Подставляя (2.6.1) и (2.6.2) в уравнение изогнутой оси балки (2.5.22), получаем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2δ |
= |
|
F(l − z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.6.3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Решение дифференциального уравнения (2.6.3) можно получить последовательным интегрированием. |
|||||||||||||||||||||||||||||||||||||||||||||
Однократное интегрирование (2.6.3) дает |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
dδ |
|
|
|
|
|
Fl |
dz − |
|
|
Fzdz |
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
|
lz − |
|
|
|
|
+C |
|
||||||||||||||||||||||
|
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
EI x |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
∫ EI x |
∫ EI x |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
(2.6.4) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
После повторного интегрирования уравнения (2.6.4) получаем выражение для нахождения перемещений |
|||||||||||||||||||||||||||||||||||||||||||||
точек в зависимости от их текущих координат: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
F |
|
|
|
z |
2 |
|
|
|
|
|
|
|
F |
|
|
|
|
lz |
2 |
|
|
|
|
z |
3 |
|
|
|
|
||||||||||||
|
|
|
|
δ = ∫ |
lz − |
|
dz + ∫C1dz = |
|
|
|
|
|
|
|
− |
|
|
|
+ C1z + C2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
EI x |
|
|
|
2 |
|
|
|
|
|
EI x |
2 |
|
|
|
|
|
|
6 |
. |
(2.6.5) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Постоянные интегрирования C1 и C2 |
можно определить, используя условия на границе: |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
dδ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ = |
0, |
|
= 0 |
при z = 0 . Из первого граничного условия получаем C2 |
|
= 0 , а из второго - C1 = 0 . После |
||||||||||||||||||||||||||||||||||||||||
dz |
|
|||||||||||||||||||||||||||||||||||||||||||||
подстановки найденных постоянных в (2.6.5) окончательно запишем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
2 |
|
|
|
|
z |
3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ = |
|
|
|
lz |
|
|
|
− |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
6 |
|
. |
|
|
|
(2.6.6) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Перемещение закрепленного конца балки соответствует z = l , следовательно, для этого конца из (2.6.6)
имеем
δ = |
Fl3 |
|
3EI x . |
|
|
|
(2.6.7) |
В качестве второго примера рассмотрим задачу расчета балки, установленной на двух опорах и нагруженной так, как это показано на рис. 2.5.4a и 2.6.2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.6.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Изгибающие моменты, действующие на участках a и b , определяются формулой (2.5.3). Тогда, |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
интегрируя уравнение изогнутой оси балки (2.6.3), получаем на участке длиной |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dδ |
|
|
|
|
|
Fb |
|
|
|
|
|
Fb |
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
= |
|
|
|
|
|
|
zdz = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ C |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫lEI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
x |
|
|
|
|
lEI |
|
x |
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
(2.6.8) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
δ |
= |
|
|
Fb |
|
z2 |
|
dz + |
|
C dz |
= |
|
|
Fb |
|
|
|
z3 |
|
+ C z + C |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∫lEI |
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
lEI |
x |
|
|
6 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
(2.6.9) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
а на участке длиной b - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dδ |
2 |
|
|
|
|
|
|
Fb |
|
|
|
|
|
|
|
F(z −a) |
|
|
|
|
|
|
Fb z2 |
|
|
|
|
F(z −a)2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
zdz |
+ |
|
|
|
|
|
|
|
|
dz = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
+ C3 |
|
|||||||||
|
|
|
dz |
∫lEI |
x |
∫ |
|
|
EI |
x |
|
|
lEI |
x |
|
|
|
2 |
|
|
|
|
2EI |
x |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, (2.6.10) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Fb z2 |
|
|
|
|
|
F(z |
− a)2 |
|
|
|
|
|
|
|
|
Fb z3 |
|
|
|
|
|
F |
|
|
(z − a)3 |
|
|
|
|
||||||||||||||||||||||||||
δ |
|
= |
|
|
|
|
|
|
|
|
dz − |
|
|
|
|
|
|
|
|
|
|
dz + |
|
C dz |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
+ C |
z + C |
|
||||||||
2 |
∫lEI |
|
|
|
|
∫ 2EI |
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|||||||||||||||||||||||||
|
|
x |
|
|
2 |
|
|
|
x |
|
|
|
|
1 |
|
|
|
|
lEI |
x |
|
|
|
6 |
|
|
|
|
|
EI |
x |
6 |
|
3 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.(2.6.11) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Для нахождения конечных зависимостей по расчету перемещений и углов поворота следует определить значения произвольных постоянных, используя очевидные условия на границах.
•Условие 1: δ1 = 0 при z = 0 , тогда из (2.6.9) следует C2 = 0 ;
|
|
dδ1 |
= |
dδ2 |
|
|
• |
Условие 2: |
dz |
dz |
при z = a , откуда с учетом (2.6.8) и (2.6.10) получаем C3 |
= C1 ; |
|
• |
Условие 3: |
δ1 |
= δ2 при z = a , тогда с помощью (2.6.9), (2.6.11) и равенства C3 = C1 имеем |
|||
|
C4 = 0 ; |
|
|
|
|
|
•Условие 4: δ2 = 0 при z = l , следовательно, используя (2.6.11), получаем
|
Fb l3 |
− |
|
|
F |
|
(l −a)3 |
+C3l = 0 C3 = − |
|
|
Fb |
|
|
(l2 −b2 ) |
|
|||||||||||||||||||||||||||||
|
lEI x |
|
|
|
6 |
|
|
|
|
6lEI x |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
EI x |
|
|
6 |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||
С учетом вычисленных констант из (2.6.9) и (2.6.11) окончательные формулы для расчета перемещений |
||||||||||||||||||||||||||||||||||||||||||||
приобретают вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
= |
Fbz |
(z2 − l2 +b2 ) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
6lEI x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
(2.6.12) |
|||
|
|
|
|
|
|
|
|
|
δ2 = |
|
|
Fbz |
|
(z2 −l2 +b2 ) − |
F |
|
|
(z −a)3 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
6lEI x |
|
EI x |
6 . |
|
|
|
(2.6.13) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Углы поворота текущего сечения на соответствующих участках согласно (2.6.8) и (2.6.10) равны |
|
|||||||||||||||||||||||||||||||||||||||||||
|
dδ |
|
|
|
|
|
Fb z2 |
|
|
|
Fb |
|
|
|
|
|
|
|
|
|
Fb |
|
|
|
l2 |
|
|
b2 |
|
|
||||||||||||||
|
1 |
|
= |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
(l2 −b2 ) |
= |
|
|
|
|
z2 − |
|
|
+ |
|
|
|
|
|||||||||||
|
|
|
lEI x 2 |
|
|
|
6lEI x |
|
2lEI x |
3 |
3 |
|
||||||||||||||||||||||||||||||||
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; (2.6.14) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dδ |
2 |
|
|
|
Fb |
|
|
|
|
l2 |
|
|
|
b2 |
|
|
F(z −a)2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
z2 − |
|
|
|
+ |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
3 |
|
3 |
|
|
2EI x |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2lEI x |
|
|
|
|
|
|
|
|
. |
|
(2.6.15) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Практический интерес представляет случай, когда внешняя нагрузка приложена симметрично относительно
опор. Тогда справедливо равенство z = a = b = l / 2 . При этом, например, средняя точка между опорами перемещается на расстояние
δ |
= |
Fl3 |
|
|
|
|
|
||
1 |
|
48EI x , |
|
|
|
|
(2.6.16) |
||
а угол поворота сечения, как и следовало ожидать, в рассматриваемой точке равен
dδ1 |
= 0 |
|
dz |
|
|
. |
(2.6.17) |
Описанный выше метод расчета перемещений можно применять только для ограниченного круга достаточно простых задач, тогда как подобный подход для более сложных случаев приводит к большим техническим трудностям. Более универсальными являются энергетические методы.
Расчет перемещений энергетическими методами. Рассмотрим равновесие тела, нагруженного системой внешних силовых факторов Fi (рис. 2.1.1). При приложении внешней нагрузки каждая точка тела перемещается в новое положение (рис. 2.1.3). Обозначим перемещения в точках приложения сил черезδi . Если принадлежащая телу точка приложения силы Fi перемещается на расстояние dδi в направлении действия Fi
(такое перемещение называется возможным), следовательно, эта сила совершает работу dWi |
, равную |
|||||||||||||||
|
|
dWi = Fi dδi . |
|
|
|
(2.6.18) |
||||||||||
В результате совершенной работы в объеме тела возникают внутренние напряжения, приводящие к |
||||||||||||||||
увеличению потенциальной энергии U деформации на величину dUi : |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
dU |
|
= |
∂ U |
dδ |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
i |
|
|
|
∂δ |
i |
|
|
(2.6.19) |
||||
|
|
|
|
|
|
|
|
|
|
i |
. |
|
|
|||
Поскольку приращение энергии деформаций dUi обеспечивается только работой dWi , т. е. левые части |
||||||||||||||||
(2.6.19) и (2.6.18) равны, то, приравнивая между собой их правые части, запишем |
|
|
|
|
||||||||||||
|
|
|
|
F = |
|
∂ U |
|
|
|
|
|
|||||
|
|
|
|
|
∂δ |
|
|
|
|
|||||||
|
|
|
|
i |
|
|
|
|
(2.6.20) |
|||||||
|
|
|
|
|
|
|
|
|
|
i . |
|
|
|
|||
Если рассматривать возможные приращения на других направлениях, то после аналогичных вычислений |
||||||||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F = |
∂ U |
|
F = |
|
∂ U |
|
F = |
∂ U |
|
|
||||||
∂δ |
|
|
∂δ |
|
|
|
|
∂δ |
|
|||||||
1 |
2 |
|
|
2 ,..., |
i |
(2.6.21) |
||||||||||
|
1 |
, |
|
|
|
|
|
|
i . |
|||||||
Из (2.6.21) следует, что величина внешней нагрузки, вызвавшей перемещение i - ой точки тела, равна частной производной потенциальной энергии по данному перемещению. Это утверждение (т. н. первая теорема
Кастилиано) может быть положено в основу расчета перемещений твердых деформируемых тел. Решение (2.6.21), полученное на основе анализа внутренней энергии деформированного тела, представимо и в иной форме:
если на тело действует система внешних сил F1 , F2 ,..., Fi , то, вычисляя частные производные от потенциальной энергии по силам, имеем
δ = |
∂ U |
|
δ |
|
= |
∂ U |
|
δ |
= |
∂ U |
|
|
∂ F |
|
∂ F |
∂ F |
|
||||||||
1 |
|
2 |
|
i |
|
(2.6.22) |
||||||
|
1 , |
|
|
|
2 ,..., |
|
|
i . |
||||
Выражение (2.6.22) представляет собой аналитическую запись второй теоремы Кастилиано.
Применим описанный выше метод к расчету перемещений свободного конца консольной балки, жестко закрепленной другим концом (рис. 2.6.1). Перемещение свободного конца (без учета поперечных сил), как следует из (2.6.22) и (2.5.33), равно
|
|
∂ U |
|
∂ |
l |
M 2 |
dz |
|
∂ |
l |
F 2 (l − z)2 dz |
|
Fl3 |
|
|
δ |
= |
|
= |
|
∫ |
nx |
|
= |
|
∫ |
|
= |
|
|
|
∂ F |
∂ F |
2EI x |
∂ F |
2EI x |
3EI x |
|
|
||||||||
|
|
|
0 |
|
0 |
|
, |
(2.6.23) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
что совпадает с (2.6.7).
Необходимо однако отметить, что в произвольном случае операция вычисления перемещений, основанная на непосредственном применении второй теоремы Кастилиано, может быть достаточно сложной технически. Более часто используется другой энергетический подход, являющийся модификацией вышеописанного - метод единичной нагрузки, или метод Мора. Рассмотрим его применительно к плоскому случаю чистого изгиба.
Дифференцирование выражения (2.5.33) в общем виде дает
|
|
∂ U |
|
|
|
∂ |
|
∫ |
M 2 dz |
= ∫ |
M |
|
∂ M nx |
dz |
|
||
δi = |
|
|
|
= |
|
|
|
nx |
nx |
|
|
|
|||||
|
∂ F |
∂ |
F |
2EI |
EI |
|
∂ F |
|
|||||||||
|
|
|
i |
|
|
|
|
i |
|
|
x |
|
x |
|
i |
. |
(2.6.24) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M1x |
= |
∂ M nx |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∂ |
F |
|
и |
M |
nx - изгибающие моменты, обусловленные |
||||||||||||
Введем следующие обозначения: |
|
|
|
i |
|
|
|||||||||||
единичной силой и полной внешней нагрузкой соответственно. Отметим, что единичную нагрузку нужно приложить так, чтобы ее направление совпадало с направлением искомого перемещения. Тогда (2.6.24) переписывается в виде
δi = |
∫ |
M nx M1x dz |
|
|
|
EI |
|
|
|
||
|
|
|
|
|
|
|
|
|
x |
. |
(2.6.25) |
Из (2.6.25) видно, что расчет перемещений сводится в конечном итоге к вычислению интегралов. А поскольку вычисление интегралов представляет собой простейшую численную процедуру, которая может быть легко реализована на компьютере, то этот метод и получил широкое распространение. Проиллюстрируем применение метода Мора на нескольких примерах.
1) Определим перемещение конца консольно закрепленной балки (рис. 2.6.1), пользуясь формулой (2.6.25). Для этого запишем выражения для двух изгибающих моментов: от рабочей нагрузки, который равен
M nx = F(l − z), и от единичной нагрузки, M1x = (l − z). Отсюда, как и следовало ожидать, получаем
l |
F(l − z) |
2 |
dz |
|
Fl3 |
|
|||
δ = ∫ |
|
= |
|
||||||
|
|
|
3EI |
|
|
|
|||
0 |
EI |
x |
|
|
|
x . |
(2.6.26) |
||
|
|
|
|
|
|||||
2) При произвольном нагружении, понимая под δi как линейное, так и угловое возможные перемещения, по аналогии с (2.6.25) имеем
|
|
|
l |
N |
Ndz |
l |
M |
x1 |
M |
nxF |
dz |
l |
M y1M nyF dz |
l |
M |
t1 |
M |
dz |
|||||
|
|
|
δi = ∫ |
1 |
|
+ ∫ |
|
|
|
+ ∫ |
|
|
|
+ ∫ |
|
|
t |
|
|
|
|||
|
|
|
EA |
|
|
EI x |
|
EI y |
|
|
|
EI p |
|
|
|
||||||||
|
|
|
0 |
o |
|
|
|
0 |
|
0 |
|
|
|
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
N |
, N |
- единичная и результирующая осевые нагрузки в текущем сечении; |
M |
x1 , |
M y1 |
и |
M nxF |
, |
|
|||||||||||||
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
- единичные и результирующие изгибающие моменты относительно одноименной оси в текущем сечении;
(2.6.27)
M nyF
M t1 , M t - единичный и результирующий крутящие моменты текущего сечения; A - площадь поперечного сечения балки.
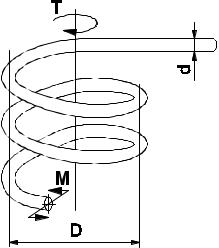
Рис. 2.6.3
3) Рассмотрим цилиндрическую пружину кручения диаметром D с числом витков i , имеющую круглое поперечное сечение диаметром d (рис. 2.6.3). Приложим к такой пружине некоторый внешний момент вращения
T . Тогда в ее поперечном сечении возникнет реактивный момент M = M nx ≡T , вызывающий появление напряжений изгиба, наибольшее нормальное значение которых, согласно (2.5.13), равно
σ |
x max |
= |
M nx |
= |
32T |
|
|
|
|
Wx |
π d 3 |
(2.6.28) |
|||
|
|
|
|||||
|
|
|
|
. |
|||
Деформированное состояние пружины характеризуется углом закручивания ϕ , т. е. относительным углом |
|||||||
поворота сечения. Для определения угла ϕ можно использовать формулу (2.6.25), полагая в ней M1x |
=1. |
||||||
Если пренебречь наличием всех иных напряжений, кроме напряжений изгиба, то при приложении внешнего момента для угла закручивания с учетом (2.3.9) получаем
πDi M |
1x |
M |
nx |
dz |
πDi Tdz |
|
π TDi |
|
64TDi |
|
|
|||||
ϕ = ∫ |
|
|
|
= ∫ |
|
= |
|
|
= |
|
|
|
|
|
||
|
EI x |
|
EI x |
|
EI x |
d |
4 |
E |
|
|
||||||
0 |
|
|
0 |
|
|
|
|
. |
(2.6.29) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Полная потенциальная энергия. Полная потенциальная энергия П любой механической системы, как известно, численно равна работе, совершенной всеми действующими на систему силами, если система
перейдет из деформированного состояния в исходное недеформированное. При этом действующими на систему силами являются как внешние нагрузки с потенциальной энергией W , так и внутренние реактивные силы,
потенциальной энергией которых является энергия деформации U .
Рассматривая переход системы от деформированного состояния к исходному недеформированному, будем считать, что точка приложения нагрузки Fi перемещается на величину δi , причем сама внешняя сила Fi
остается в процессе перехода постоянной. Работа всех k внешних сил в этом случае равна
W = −∑k |
Fiδi |
|
|
i=1 |
|
. |
(2.6.30) |
Тогда |
|
|
|
Π =U +W =U −∑k |
Fiδi |
|
|
|
i=1 |
. |
(2.6.31) |
Знак минус в (2.6.31) берется потому, что работа внешних сил и потенциальная энергия деформаций имеют различные направления. Если продифференцировать (2.6.31) по одному из возможных перемещений δi , получим
|
∂ Π |
= |
∂ U |
|
− F |
|
|
|
|
|
|
. |
|
(2.6.32) |
|||
|
∂δi |
∂δi |
|
|||||
|
|
|
|
|
i |
|
|
|
Подставляя в (2.6.32) выражение (2.6.20), имеем |
|
|
|
|
|
|
||
|
|
|
|
|
∂ Π |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂δ |
|
(2.6.33) |
|
|
|
|
|
|
i |
|
. |
|
Полная потенциальная энергия механической системы является ее важной характеристикой. Поскольку, как следует из (2.6.33), первые производные от полной энергии находящейся в равновесии системы по каждому из возможных перемещений оказываются равными нулю,
∂ Π |
= 0 |
|
∂ Π |
= 0 |
|
∂ Π |
= 0 |
|
|
|
|
|
|
|
|
|
|||
∂δ |
, |
∂δ |
2 |
|
∂δ |
(2.6.34) |
|||
1 |
|
|
|
, ,,, i |
. |
||||
то это означает, что в этом положении энергия системы достигает своего экстремального значения (в данном случае - минимума). Вывод, который следует из выражения (2.6.34), обосновывает одно из фундаментальных положений механики, и в частности, механики деформированного тела - так называемый принцип наименьшего
действия, согласно которому можно утверждать, что в условии равновесия деформированное тело принимает такое положение, при котором его полная потенциальная энергия имеет минимальное значение. Это утверждение можно отнести также и к геометрии деформированного состояния. В процессе деформации каждая точка тела занимает такое положение, при котором его полная потенциальная энергия минимальна, причем это положение является единственно возможным.
Определение перемещений статически неопределимых стержневых систем. Механическая стержневая конструкция, как считается статически неопределимой, если число внутренних силовых факторов (реакций) превышает число возможных независимых уравнений статического равновесия (см. главу 2.2 ). Исходя из определения балка, изображенная на рис. 2.6.4a, однократно статически неопределима. Если в этой статически неопределимой системе удалить одну из опор, например, среднюю (рис. 2.6.4b), то она становится статически определимой.
a)
b)
Рис. 2.6.4
Стержневые системы следует разделять на геометрически замкнутые и геометрически разомкнутые. Такое деление связано с особенностями статической неопределимости. Например, стержневая система, образованная замкнутой цепью жестко связанных элементов, представляет собой статически неопределимую рамную конструкцию (рис. 2.6.4с).
В общем случае раскрыть статическую неопределимость помогают приемы, в основу которых положены методы расчета деформаций. Для того чтобы систему из статически неопределимой преобразовать в статически
определимую, необходимо отбросить лишние связи, заменив их неизвестными реакциями X1 , X 2 ,..., X k . Величины этих реакций подбираются исходя из граничных условий. Для абсолютно жестких опор в качестве
граничного можно использовать, к примеру, условие равенства нулю перемещений точек расположения опор в направлениях соответствующих реакций. Кроме этого, допустимо утверждать, что при использовании метода сечений для замкнутого контура относительное перемещение точек приложения внутренних силовых факторов также равно нулю. Если использовать принцип суперпозиции (независимого действия сил), то аналитически условие равенства относительных перемещений запишется в виде системы линейных уравнений
δ1 X 1 |
+ δ1 X 2 |
+ δ1 X 3 |
+ . . + δ1F |
= 0 |
|
|
|
|||||
δ2 X 1 |
+ δ2 X 2 |
+ δ2 X 3 |
+ . . + δ2 F |
= 0 |
|
|
|
|||||
|
|
|
||||||||||
|
. |
. |
. |
. |
. |
. . . . |
|
. |
. . |
|
|
|
|
|
|
|
|
||||||||
δ |
kX 1 |
+ δ |
kX 2 |
+ δ |
+ . . + δ |
kF |
= 0 |
|
|
|
||
|
|
|
ik 3 |
|
|
|
|
. |
(2.6.35) |
|||
|
|
|
|
|
|
|
|
|
|
|
||
Здесь δ iX j и δ iF , i, j =1,K, k - перемещения в направлении реакции |
Xi , обусловленные силой |
|||||||||||
X j и внешними силами F соответственно. Представим перемещение δ iX j |
как произведение |
|
|
|||||||||
|
|
|
|
δ iX |
j = δij X j , |
|
|
|
|
(2.6.36) |
где δ ij - перемещение в направлении силового фактора |
Xi , вызванное действием единичной |
j -ой силы. В |
||||||||
этих обозначениях систему уравнений (2.6.35) можно переписать в виде |
|
|
|
|
|
|||||
δ11 X1 |
+ δ12 X 2 |
+ δ13 X 3 |
+ . . + δ1F |
= 0 |
|
|
||||
δ21 X1 |
+ δ22 X 2 |
+ δ23 X3 |
+ . . + δ2 F |
= |
0 |
|
|
|||
|
|
|||||||||
. |
. |
. |
. |
. |
. . . . |
. |
. |
. |
|
|
|
|
|||||||||
δk1 X1 |
+ δk 2 X2 |
+ δk 3 X3 |
+ . . + δkF |
= |
0 |
|
|
|||
|
. (2.6.37) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Решение системы уравнений (2.6.37) относительно реакций опор X1 , X 2 ,..., X k |
позволяет определить |
|||||||||
величины неизвестных реакций. Таким образом, раскрытие статической неопределимости свелось к расчету нагрузок в опорах. Такой метод получил название метода сил. Этот метод не единственный, но он является наиболее распространенным. В частности, метод сил широко используется при расчете металлоконструкций произвольной геометрической формы.
Практическое применение метода расчета статически неопределимых систем рассмотрим на примере рамы, состоящей из двух независимых участков CB и BA одинаковой длины a с постоянным поперечным
сечением (2.6.5a). Участок CB нагружен распределенной нагрузкой q . Эта рамная конструкция оказывается дважды статически неопределимой, так для определения неизвестных реакций опор не хватает двух уравнений.
Отбросим одну из опор, как показано на рисунке. Для того чтобы получить статически определимую конструкцию,
вместо отброшенной опоры следует приложить неизвестные реакции X1 |
и X 2 (рис. 2.6.5b), которые согласно |
|||||||||
(2.6.37) определяются из системы уравнений |
|
|
|
|
|
|
||||
|
|
|
|
δ11 X1 |
+ δ12 X 2 |
+ δ1F |
= 0 |
|
|
|
|
|
|
|
δ21 X1 |
+ δ22 X2 |
+ δ2 F |
= |
|
|
|
|
|
|
|
0 |
. |
(2.6.38) |
||||
|
|
|
|
|
|
|
|
|
||
Коэффициенты |
δij |
, |
i, j =1,2 |
уравнения (2.6.38), которые представляют собой перемещения, |
|
|||||
|
|
|
||||||||
вызванные единичными силами, можно определить методом Мора, записав выражения для изгибающих моментов от этих силовых факторов. При этом для упрощения записи индекс ” n ” в обозначении внутреннего изгибающего
момента будем опускать. Так, M1X 1 и |
M1X 2 - изгибающие моменты от единичной нагрузки, приложенные в |
направлениях силовых факторов X1 и |
X 2 соответственно. Графическое представление зависимости этих |
изгибающих моментов от координаты z текущего сечения приведено на рис. 2.6.5 c,d.
