
Основы проектирования машин / ГЛАВА 2.7. НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ
.pdf
ГЛАВА 2.7. НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ. ТЕОРИЯ ПРЕДЕЛЬНЫХ НАПРЯЖЕННЫХ СОСТОЯНИЙ
Напряженное состояние в точке. Внешние силы , приложенные к телу, вызывают появление в нем напряжений и деформаций. Для того чтобы можно было судить о статической прочности тела,
нагруженного произвольной системой силовых факторов, необходимо описать напряженное состояние в каждой его точке, т. е. определить совокупность напряжений, возникающих во множестве площадок, проходящих через исследуемые точки.
В общем случае напряженное состояние каждой точки деформированного тела можно описать, используя метод сечений (см. главу 2.2 ).
Рис. 2.7.1
Для анализа напряженного состояния тела в произвольной точке A выделим шестью сечениями в ее
окрестности элементарный параллелепипед с гранями (рис. 2.7.1). Полное напряжение, возникающее в каждой секущей площадке, произвольно направлено в пространстве, но в любом случае его можно представить в
виде проекций на три взаимно перпендикулярных оси, одна из которых совпадает с направлением нормали к поверхности грани, а две другие лежат в ее плоскости. Напряжение, нормальное к поверхности, называется нормальным, в то время как два других - касательными. Вращением элемента объема его грани можно разместить так, что к ним будут приложены только нормальные напряжения, а их касательные составляющие станут равными нулю. Таким образом, грани элемента будут совпадать с главными площадками, а действующие на них напряжения
–с главными напряжениями. Эти три главных напряжения полностью характеризуют напряженное состояние точки,
аего расчет в общем виде сводится к определению этой тройки напряжений.
Определение местоположения главных площадок при произвольном характере нагружения - процесс непростой, требующий дополнительных вычислений. Однако на практике почти всегда положение одной из главных площадок в заданной точке можно указать заранее. Тогда две другие главные площадки, разумеется, выбираются из множества перпендикулярных к первой. Этот прием существенно облегчает решение задачи определения главных напряжений.
a) |
b) |
c) |
Рис. 2.7.2
Если в окрестности какой-либо точки тела действуют все три главных напряжения, то имеет место трехосное нагружение, а соответствующее напряженное состояние в этой точке называется объемным (рис. 2.7.2
a). Когда же напряжения на одной из граней равны нулю, то напряженное состояние становится плоским (рис. 2.7.2 b). Наконец, в случае простейшего вида деформации (например, растяжения или сжатия), при котором только одно из главных напряжений отлично от нуля, наблюдается линейное напряженное состояние (рис. 2.7.2 с).
Рис. 2.7.3
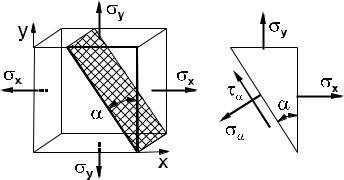
Рассмотрим наклонную секущую площадку, расположенную под углом α (рис. 2.7.3). Вне зависимости от угла наклона эта площадка будет параллельна одной из главных осей (в данном случае оси z ). На
рассматриваемой площадке кроме нормальных напряжений σα действуют также и касательные напряженияτα . Выделенный элемент будет находиться в равновесии, если суммы сил в проекциях на направления нормали и
касательной к площадке будут равны нулю, а именно
σα Aα = σx Ax cosα +σy Ay sin α ,
|
|
|
|
|
τα Aα = σx Ax |
sinα −σy Ay cosα |
(2.7.1) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
||
где Ax , Ay , Aα - площади соответствующих граней, причем |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Ay = Axtgα |
A |
= A / cosα |
. |
(2.7.2) |
|||||
|
|
|
|
|
|
, |
α |
x |
|
|
|
|||
С учетом (2.7.2) из (2.7.1) получаем |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
σα |
= σx cos2 α +σy sin |
2 α |
|
|
|||||
|
|
|
|
|
|
|
|
|
, |
|
|
|||
|
|
|
|
|
τα = (σx −σy ) sinα cosα |
|
(2.7.3) |
|||||||
|
|
|
|
|
|
|
|
|
. |
|
||||
|
|
|
|
|
|
|
cos2 α = |
|
1 |
(1 + cos2α) |
|
|||
Пользуясь известными тригонометрическими соотношениями |
2 |
, |
||||||||||||
|
|
|
|
|||||||||||
sin2 α = |
1 |
(1−cos2α) |
sinαcosα = |
1 |
sin2α |
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
||||||
2 |
|
и |
|
, преобразуем далее (2.7.3) к виду |
|
|||||||||
σα = |
1 |
(σ x +σ y ) + |
1 |
(σ x −σ y )cos2α |
||
|
2 |
|
|
|
2 |
, |
|
|
τα = |
1 |
(σ x |
−σ y )sin2α |
|
|
|
|
2 |
|
|
. |
Из (2.7.4) ясно, что наибольшие касательные напряжения τα max достигаются при значении α = |
π |
2 |
равны
(2.7.4)
и
|
|
|
|
|
|
|
τα max = |
1 |
(σx −σ y ) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
(2.7.5) |
|
Переобозначим главные напряжения |
σ |
σ y |
в порядке возрастания как |
σ |
1 и |
σ |
3 . Исключив из (2.7.4) |
|||||||||||
|
x и |
|
|
|
||||||||||||||
угол α , получим выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
(σα − |
σ1 +σ3 )2 |
+τα 2 = (σ1 −σ3 )2 |
, |
(2.7.6) |
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|||
которое в координатах σα , τα |
|
|
|
|
|
|
|
|
τ |
α max |
= σ1 −σ3 |
|
||||||
представляет собой уравнение окружности радиуса |
|
|
|
2 |
с |
|||||||||||||
|
|
|
|
|
||||||||||||||
|
σ |
|
+ |
σ |
3 ; |
τα = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
σα = |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
центром в точке |
|
|
|
|
|
|
. Полученный круг называется кругом Мора. Пример такого круга |
|||||||||||
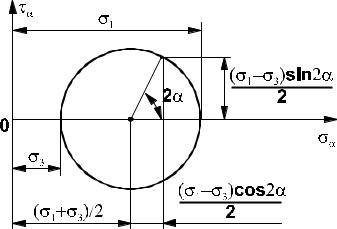
для семейства площадок, параллельных главной площадке наибольшего напряженияσ2 , представлен на рис. 2.7.4.
Рис. 2.7.4 |
Использование кругов Мора позволяет легко определить величины нормальных и касательных напряжений, приложенных к наклонным площадкам. При такой геометрической интерпретации ясно, что каждой секущей площадке, наклоненной под определенным углом, соответствует точка на круге Мора. Текущие напряжения на
площадке, наклоненной под углом α , равны координатам точки, которая лежит на пересечении этого круга с
прямой, проведенной под углом 2α (рис. 2.7.4).
Рассмотренный выше подход к описанию плоского напряженного состояния наклонной площадки,
находящейся в плоскости оси z , можно распространить и на площадки, лежащие в других плоскостях. Очевидно, что каждая из этих площадок характеризуется парой главных напряжений, а напряженное состояние на любой
наклонной площадке в случае трехосного нагружения определяется совокупностью трех кругов напряжений (рис. 2.7.6). Можно доказать, что координаты точек заштрихованной области равны нормальным и касательным напряжениям на произвольно ориентированных площадках.
Обобщенный закон Гука и потенциальная энергия деформации. Рассматривая нормальные нагружения и нагружения сдвига, можно выявить зависимость между компонентами напряженного (напряжениями
σ и τ ) и деформированного (линейными ε и угловыми γ деформациями) состояний и тем самым записать выражение для обобщенного закона Гука (см. 2.2.6 - 2.4.12). Применительно к случаю плоского напряженного
состояния закон Гука записывается в виде
εx |
= |
1 |
|
|
(σx − µσ y ) |
||||||||||
|
E |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
ε |
|
= |
|
(σ |
|
|
− µσ |
|
) |
||||||
|
|
E |
|
|
|
|
|||||||||
|
y |
|
|
|
|
|
y |
|
|
|
x |
|
|||
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
|
|
ε |
|
= − |
|
(σ |
|
+σ |
|
) |
|||||||
z |
|
E |
x |
y |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
γ xy |
= |
τxy |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
G |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Для случая объемного напряженного состояния имеем
εx = |
|
1 |
|
[σx − µ(σ y +σz )] |
|
|
|
||||||
|
E |
|
|
||||||||||
|
|
|
|
|
[σ y − µ(σx +σz )] |
|
|
|
|||||
|
|
|
|
1 |
|
|
|
||||||
εy = |
|
|
|
|
|||||||||
E |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
[σz − µ(σx +σ y )] |
|
|
|
||||
εz = |
|
|
|
|
|
||||||||
|
E |
|
|
|
|||||||||
|
τxy |
|
|
τyz |
|
τ |
|
|
|||||
γ xy = |
|
, |
|
γ yz = |
, γ zx = |
zx |
|
||||||
|
|
|
|
|
|
|
|
|
|||||
G |
|
|
G |
|
G |
||||||||
|
|
|
|
|
|
|
, |
||||||
где
(2.7.7)
(2.7.8)
εx = ∆dx εy = ∆dy |
εz = |
∆dz |
|
|||||
|
dx |
; |
dy |
; |
dz . |
(2.7.9) |
||
Относительная объемная деформацияεV элемента объема dV = dxdydz равна |
|
|||||||
∆dV = |
(dx +∆dx)(dy +∆dy)(dz +∆dz) |
|
|
|||||
εV = dV |
|
|
dxdydz |
, |
(2.7.10) |
|||
или, с учетом (2.7.9), |
|
|
|
|
|
|
||
|
εV |
= (1+εx )(1+εy )(1+εz ) |
(2.7.11) |
|||||
|
|
|
|
|
|
. |
|
|
Обозначим через V объем тела до, а через V1 - после деформации. Выполнив в правой части (2.7.11) |
||||||||
операцию умножения и отбросив члены выше первого порядка, получаем выражение для относительного |
|
|||||||
изменения объема θ , |
|
|
|
|
|
|
||
θ = |
V1 −V |
|
= |
εV V −V |
= εV −1 = εx +εy +εz |
|
||
V |
V |
|
||||||
|
|
|
. |
(2.7.12) |
||||
Потенциальная энергия деформации элемента объема в общем случае нагружения, как известно, равна сумме элементарных работ всех сил, распределенных по поверхности этого объема, т. е.
dU = |
1 |
(σxεx +σ yεy +σzεz +τxyγ xy +τyzγ yz +τzxγ zx )dxdydz |
|
2 |
|||
|
. (2.7.13) |
Выражая в (2.7.13) деформации через напряжения по формулам (2.7.8), запишем
|
1 |
2 |
|
|
2 |
|
2 |
|
|
|
1 |
2 |
2 |
2 |
|
|
dU = |
|
[σx |
|
+σy |
|
+σz |
−2µ(σyσz +σzσx +σxσy )]+ |
|
(τyz |
+τzx |
+τxy |
) dxdydz |
||||
2E |
|
|
2G |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.7.14) |
или в главных напряжениях |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
dU = |
|
1 |
[σ1 |
2 +σ2 |
2 +σ3 |
2 −2µ(σ2σ3 +σ3σ1 +σ1σ2 )]dxdydz |
||||||||
|
|
2E |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. (2.7.15) |
|||
Очевидно, что полная потенциальная энергия определится суммированием энергий элементарных объемов:
U = ∫dU
V |
. |
(2.7.16) |
Теория предельных напряженных состояний. Как известно, механическое состояние тела главным образом определяется напряжениями, возникающими вследствие его нагружения. При малых действующих силах материал проявляет упругие свойства, а при повышении нагрузки у него появляются необратимые пластические деформации, величины которых растут по мере увеличения внешних силовых факторов. Пластические деформации характерны только для пластичных материалов, к которым следует отнести большинство сталей, используемых в производстве машин. Пластическое деформирование приводит вначале к взаимному смещению слоев металла, затем происходит зарождение трещин и, наконец, наступает разрушение,
или потеря прочности.
Состояние, при котором внутренние изменения в металле приводят к его разрушению, называется
предельным напряжением, или предельным напряженным состоянием. Под предельным напряженным состоянием хрупких материалов понимается начало их разрушения, а пластичных - возникновение необратимых пластических деформаций. Вывод о надежности любой проектируемой конструкции следует делать на основании сопоставления максимальных напряжений, которые могут возникнуть в наиболее опасной точке, и предельно допустимых для данного материала. Предельное напряженное состояние детали или конструкции является той границей, за которой недопустима их эксплуатация. Надежность работы оказывается тем выше, чем дальше от предельного состояния уровень фактических напряжений внутри материала детали. Это обстоятельство говорит о важности расчета параметров, характеризующих предельное напряженное состояние рассматриваемого объекта.
Для численной характеристики статической прочности обычно используют понятие запаса прочности. На решении этой проблемы следует остановиться более подробно.
За коэффициент запаса данного напряженного состояния принимается число, показывающее, во сколько раз нужно увеличить все параметры напряженного состояния, чтобы оно стало предельным. Важным понятием при расчетах на прочность является понятие равнопрочности. Два разнотипных напряженных состояния считаются равнопрочными, если они вызывают равную вероятность статического разрушения, т. е. равны коэффициенты запаса этих состояний. Фактическое напряженное состояние тела можно сравнивать, например, с одноосным растяжением (сжатием), так как этот вид деформации является наиболее доступным и простым испытанием. Напряжение растяжения, которое вызывает в образце такую же вероятность разрушения, что и фактическое
напряженное состояние, называется эквивалентным. Эквивалентное напряжение σe является функцией главных напряжений, что можно коротко записать в виде
|
|
|
|
|
σe |
= f (σ1 ,σ2 ,σ3 ) . |
(2.7.17) |
Очевидно, что наиболее опасной является такая точка элемента конструкции, в которой эквивалентное |
|||||||
напряжение σe достигает максимального значения. Условие прочности в таком случае записывается в |
|
||||||
следующем виде: |
|
|
|
|
|
||
σ |
e |
≤ σb |
=σ |
ab |
|
|
|
|
nb |
|
|
|
|
||
• |
|
|
- |
для хрупких материалов; |
(2.7.18) |
|
|
σ |
e |
≤ σr |
=σ |
ar |
|
|
|
|
nr |
|
|
|
|
||
• |
|
|
- |
для пластичных. |
(2.7.19) |
|
|
σab σar |
nb nr |
Здесь σab и σar - допускаемые напряжения по пределам прочности и текучести соответственно, nb и nr
- коэффициенты запаса прочности и текучести, σb и σr - пределы прочности и текучести.
Однозначно сформулировать критерии равнопрочности не удается, поэтому существует несколько теорий, которые взаимно дополняют друг друга и могут быть применены для различных материалов и условий их нагружения. Например, для хрупких материалов рекомендуется использовать теорию наибольших нормальных напряжений (наибольших растягивающих деформаций). Эти рекомендации сформулированы на основе многочисленных лабораторных испытаний образцов, изготовленных из разных материалов.
Рассмотрим последовательно каждую из существующих теорий, определяющих предельное состояние, и укажем границы их рационального применения. Читателя не должно удивлять то обстоятельство, что различные теории при описании предельного состояния приводят к разным результатам - это еще раз говорит о приближенности гипотез прочности.
Гипотеза наибольших нормальных напряжений (первая теория прочности). Согласно первой теории прочности, два напряженных состояния считается равнопрочными, если равны их наибольшие напряжения растяжения,
σe =σ1 . |
(2.7.20) |
Эта гипотеза основывается на том очевидном факте, что наибольшее влияние на процесс разрушения оказывают максимальные главные напряжения, которые вызывают разрыв межмолекулярных связей. Два других главных напряжения при этом в расчет не принимаются. Как показали лабораторные испытания, наличие других главных напряжений может существенно повлиять на прочность. Однако в том случае, если другие главные напряжения много меньше максимальных, эта гипотеза может быть с успехом использована, но только при расчетах деталей из хрупких материалов. Для остальных же случаев ее применение необоснованно.
Гипотеза наибольших нормальных деформаций (вторая теория прочности). Если предположить,
что разрушение происходит в результате отрыва, вызванного чрезмерным уровнем относительного удлинения, то можно сформулировать вторую теорию прочности, согласно которой условие равнопрочности выполняется в том случае, когда равны относительные линейные деформации
εe = ε1 , |
(2.7.21) |
где εe и ε1 - линейные деформации растяжения при эквивалентной и наибольшей рабочей нагрузках |
|
соответственно. Уравнение второй теории прочности, записанное через напряжения, принимает вид |
|
σe =σ1 − µ(σ2 +σ3 ) . |
(2.7.22) |
Как видно из (2.7.22), при определении эквивалентных напряжений учитываются все напряжения, а не только главные. Второй теорией можно описывать прочность некоторых неметаллических материалов. Однако эта теория, как и первая, не имеет достаточного экспериментального подтверждения. Ее применение дает лучшие результаты для хрупких материалов.
Гипотеза наибольших касательных напряжений (третья теория прочности). Теория наибольших касательных напряжений используется для описания прочности пластических материалов, к каковым, как уже говорилось выше, относится большинство металлов. Для хрупких материалов эта гипотеза не применима.
Основанием для формулировки гипотезы наибольших касательных напряжений является предположение,
что при растяжении цилиндрические образцы разрушаются по площадкам, наклоненным под углом в π / 4 . Как было показано в главе 2.2 , на этих же площадках действуют наибольшие касательные напряжения. Согласно
теории наибольших касательных напряжений два напряженных состояния являются равнопрочными, если равны их наибольшие касательные напряжения, т. е.
σe =σ1 −σ3 = 2τ . |
(2.7.23) |
Здесь под τ понимается максимальное значение касательного напряжения (2.7.5).
Главный недостаток гипотезы наибольших касательных напряжений заключается в том, что при ее использовании не учитывается влияние средних главных напряжений, которые так или иначе участвуют в процессе
разрушения. Например, пренебрежение напряжениямиσ2 , как показали испытания, в отдельных случаях может
привести к ошибке порядка (10 ÷15)% , что необходимо помнить при выборе значений коэффициентов запаса прочности.
Энергетическая гипотеза (четвертая теория прочности). Очевидно, что при нагружении тела внешней нагрузкой увеличивается его потенциальная энергия. Казалось бы, при определенном уровне потенциальной энергии должно произойти разрушение. Однако, как следует из результатов экспериментов, при нагружении образца одинаковой сжимающей силой в трех взаимно перпендикулярных плоскостях даже при неограниченном возрастании внутренней потенциальной энергии разрушения материала все же не происходит. Можно сказать, что в этом случае изменение объема не приводит к изменению формы. Следовательно, опасное состояние связано не с энергией изменения объема, а с энергией формоизменения. В соответствии с энергетической теорией два напряженных состояния считаются равнопрочными, если они имеют одинаковые энергии формоизменения. Достоинством этой теории является то, что при расчетах учитываются все главные
напряжения. Погрешность вычислений по этой теории не превышает 15% .
Рассмотрим деформацию элементарного кубика (рис. 2.2.10). В общем случае нагружения полная потенциальная энергия деформации кубика dU складывается из энергия формоизменения dU f и энергии изменения объема dUV , так что
|
|
dU f |
|
= dU −dUV |
. |
|
|
(2.7.24) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Как было показано в (2.2.13), в терминах главных напряжений полная потенциальная энергия деформации |
|||||||||||||
кубика dU равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
dU = |
1 |
(σ ε |
1 |
+σ |
2 |
ε |
2 |
+σ |
3 |
ε |
3 |
)dxdydz |
|
|
|
||||||||||||
2 |
1 |
|
|
|
|
. |
(2.7.25) |
||||||
|
|
|
|
|
|
|
|
|
|
||||
Форма элемента не изменится только в том случае, если напряжения, приложенные к его граням, равны |
|||||||||||||
между собой. Тогда можно записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
σ1 =σ2 =σ3 =σm , |
|
ε1 = ε2 = ε3 = εm , |
|
||||||||||
σm = (σ1 +σ2 +σ3 ) / 3, |
|
εm = (ε1 +ε2 +ε3 ) / 3 , |
(2.7.26) |
||||||||||
причем полная энергия деформации становится равной энергии изменения объема, dU = dUV . Выражение (2.7.25) с учетом (2.7.26) приводится к виду
|
|
|
|
|
dUV |
= |
|
1 |
(3σmεm )dxdydz |
|
|||
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
. |
(2.7.27) |
|||
|
Подстановка (2.7.25) и (2.7.27) в (2.7.24) дает выражение для расчета энергии формоизменения элемента |
||||||||||||
объема: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dU f = |
1 + µ |
[(σ1 −σ2 )2 |
+(σ2 −σ3 )2 |
+(σ3 −σ1 )2 |
]dxdydz |
||||||
|
|
|
|||||||||||
|
|
|
6E |
|
|
|
|
|
|
|
|
. (2.7.28) |
|
|
Для одноосного напряженного состояния, при котором |
σ1 = σe, σ2 = σ3 |
= 0 |
||||||||||
|
|
|
|
|
|
|
, энергия изменения |
||||||
формы |
dU f |
, согласно (2.7.28), равна |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
dU f |
= |
|
1 + µ |
σe dxdydz |
|
|||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
3E |
. |
(2.7.29) |
||
Приравнивая правые части (2.7.28) и (2.7.29), находим
|
|
|
|
|
|
σe = |
1 |
(σ1 −σ2 )2 |
+(σ2 −σ3 )2 +(σ3 −σ1 )2 |
|
|||
|
|
|
|
|
|
|
2 |
|
|
|
|
. |
(2.7.30) |
Переход в (2.7.30) от главных напряжений к текущим дает |
|
|
|
|
|||||||||
|
|
|
σe |
= 1 |
(σ x −σ y )2 |
+(σ y −σ z )2 +(σ z −σ x )2 +6(τ2yz +τ2zx +τ2xy ) |
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
. |
(2.7.31) |
|
В частном случае плоского напряженного состояния (одноосное растяжение со сдвигом), когда |
|
||||||||||||
σ x =σ y = 0 |
σ |
z |
=σ |
, |
τ xy |
=τ zx = 0 τ zy =τ |
, выражение (2.7.31) переписывается в виде |
|
|||||
, |
|
|
|
, |
|
|
|||||||
|
|
|
|
|
|
|
|
σ |
e |
= |
σ2 +3τ2 |
(2.7.32) |
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
Если далее положить в (2.7.32) σ = 0, т. е. рассматривать напряженное состояние в форме чистого |
|||||||||||||
сдвига, то получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ = |
|
1 |
σe ≈ 0,577σe |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
. |
(2.7.33) |
Поскольку первые признаки пластического деформирования появляются тогда, когда эквивалентные напряжения становятся равными пределу текучести, то значение предела текучести при сдвиге можно рассчитывать по формуле
τr = |
1 |
σr ≈ 0,577σr |
|
|
3 |
, |
(2.7.34) |
что хорошо согласуется с экспериментальными данными. Эксперименты показали, что первые пластические
деформации появляются в материале при напряжениях, равных (0,56 ÷0,6)σr , то есть теория энергии формоизменения наиболее близка к экспериментальным данным и может быть использована для описания
прочности упруго - пластических материалов. Отметим, что, согласно (2.7.23), теория наибольших касательных напряжений приводит к результату
τr = 0,5σr , |
(2.7.35) |
близкому к (2.7.34), но менее точному.
В заключение следует заметить, что все вышеописанные теории прочности неприменимы к анизотропным материалам, прочность которых, помимо всего прочего, зависит от направления приложения внешней нагрузки.
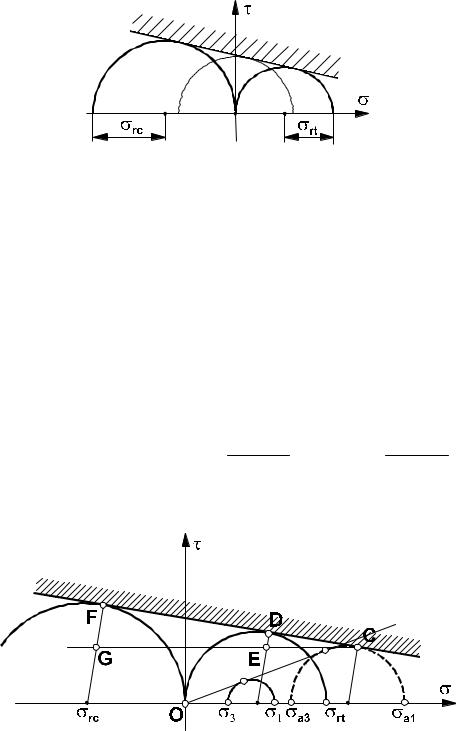
Теория предельных состояний (теория Мора). Как уже говорилось, наиболее простым с точки зрения практической реализации является испытание материалов на растяжение (сжатие). В случае предельного
растяжения можно ограничиться напряжением, равным значению предела текучести при растяжении σrt , а в
случае предельного сжатия - пределом текучести при сжатииσrc . Круги Мора, соответствующие этому случаю, изображены на рис. 2.7.5. Все остальные напряженные состояния будут находиться внутри этих двух предельных.
Логично предположить, что граница предельного состояния совпадает с огибающей двух предельно допустимых, и она линейна. Случаи фактического нагружения будут считаться безопасными с точки зрения прочности, если их наибольшие напряжения не превосходят граничных значений.
|
Рис. 2.7.5 |
|
|
|
|
|
|
|
Поскольку фактическое нагружение характеризуется двумя главными наибольшими напряжениями σ1 и |
||||||||
σ3 , то, полагая коэффициент запаса равным n , можно с помощью (2.7.18) - (2.7.19) определить предельные |
||||||||
значения σa1 и σa3 этих напряжений: |
|
|
|
|
|
|
|
|
|
|
σa1 = nσ1 ; |
σa 3 = nσ3 . |
|
|
(2.7.36) |
||
Предельный круг Мора на рис. 2.7.6 изображен пунктиром. Проведя из точки C горизонталь, запишем |
||||||||
|
|
|
DE = |
FG |
|
|
|
|
|
|
|
CE |
CG . |
|
|
(2.7.37) |
|
Очевидно, что величины отрезков DE , |
FG , CE и CG можно представить в виде |
|
|
|||||
DE = |
σrt − σa1 −σa3 |
FG = |
σrc − σa1 −σa3 |
|
||||
|
2 |
2 |
; |
|
2 |
2 |
; |
|
CE = |
σa1 +σa3 |
− σrt |
CG = |
σa1 +σa3 |
+ |
σrc |
|
|
|
2 |
2 |
; |
|
2 |
|
2 . |
(2.7.38) |
|
Рис. 2.7.6 |
|
|
|
|
|
|
|
Тогда, подставляя (2.7.38) в (2.7.37) и разрешая пропорциональное уравнение относительно предела |
||||||||
текучести при растяжении, получаем |
|
|
|
|
|
|
|
|
σ |
rt |
= σ |
a1 |
− |
σrt |
σ |
a3 |
|
|
σ |
rc |
|
|||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
. |
(2.7.39) |
|
Значение коэффициента запаса при этом, как следует из (2.7.36), определяется выражением
|
|
n = |
|
|
σrt |
|
|
|
|
||
|
|
|
|
|
σrt |
|
|
|
|
||
|
|
σ |
1 |
− |
σ |
3 |
|
|
|||
|
|
σ |
rc |
|
(2.7.40) |
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
. |
|||
Коэффициент запаса прочности для эквивалентного растяжения |
|
|
|
|
|
|
|
||||
|
|
|
|
n = |
σrt |
|
|
|
|
||
|
|
|
|
|
|
σe |
. |
|
|
(2.7.41) |
|
Так как коэффициенты запаса рассматриваемого и эквивалентного напряженных состояний по |
|
||||||||||
определению равны, то имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
σe =σ1 − kσ3 , |
(2.7.42) |
||||||||
k = |
σrt |
σrt |
|
|
|
|
|
σbt |
|
||
где |
σrc . Для хрупких материалов вместо |
σrc следует брать отношение σbc . |
|
||||||||
Теорию Мора рекомендуется использовать, если материалы по-разному работают на растяжение и сжатие. В том случае, когда механические характеристики при растяжении и сжатии совпадают, то результаты расчета по теориям Мора и наибольших касательных напряжений, как это следует из (2.7.42), приводят к одинаковым результатам. Недостатком обеих этих теорий является то, что эквивалентное напряжение рассчитывается без
учета главного напряжения σ2 .
