54. Система линейных однородных уравнений.

Согласно определению 4.2 запишем однородную систему линейных уравнений.

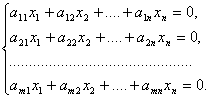     (7.1).

 

Однородная система всегда совместна, так как всегда имеется тривиальное решение.

Согласно общей теории, если  , то единственным является тривиальное решение.

Если же  , то решений бесконечно много, и все они, кроме одного, нетривиальные.

 

Теорема 7.1 (о нетривиальных решениях однородной системы)

Однородная линейная система с квадратной матрицей  имеет нетривиальное решение тогда и только тогда, когда определитель системы равен нулю.

 

Доказательство

По теореме Крамера (5.1)   тогда и только тогда, когда система с квадратной матрицей имеет единственное решение (т.е. векторы – столбцы системы (7.1) – линейно зависимы). В случае если задана система линейных однородных уравнений, это решение – тривиальное  (0,0,…0). Значит, нетривиальные решения имеются тогда и только тогда, когда   (т.е. решений системы бесконечное множество).

 

Любое решение СЛОУ выражается в виде линейной комбинации

 векторов (если  ):

 

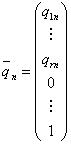, …,  .           (7.2)

Покажем, что вектора   – линейно независимы. Для этого составим матрицу   из их координат:

.

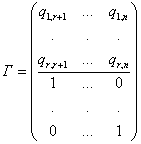Ниже черты расположен минор порядка  , отличный от нуля         столбцов матрицы   линейно независимы.

Следовательно, вектора   – линейно независимы, т.е. эти вектора образуют базис подпространства.

 

Определение 7.1

Всякая линейно независимая система   решений системы линейных однородных уравнений  называется фундаментальной системой решений.

 

Замечание 1. Отличный от нуля минор матрицы порядка  , такой, что всякие миноры порядка   и выше, (если такие имеются) равны нулю, называется базисом.

Итак, общее решение СЛОУ:

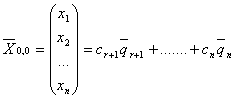                   (7.3),

где   - фундаментальная система решений,

 - произвольные постоянные.

55. Эквивалентные системы уравнений. Элементарные преобразования уравнений системы. Метод Гаусса.

Две системы, множества решений которых совпадают, называются эквивалентными или равносильными (совпадение множеств решений означает, что каждое решение первой системы является решением второй системы, и каждое решение второй системы является решением первой).

Две несовместные системы считаются эквивалентными.

Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Эквивалентными преобразованиями являются: а) умножение обеих частей уравнения на число, отличное от нуля, б) прибавление к одному уравнению другого уравнения. Очевидно, что прибавление к одному уравнению другого уравнения, умноженного на какое-либо число, также является эквивалентным преобразованием. Эквивалентность преобразований а) и б) читателю предлагается доказать самому. Также читателю предлагается доказать самому, что с помощью преобразований а) и б) можно получить новую систему, которая будет отличаться от исходной только тем, что в новой системе два любых уравнения исходной системы переставлены местами.

  К элементарным преобразованиям относятся:

            1)Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.

            2)Перестановка уравнений местами.

            3)Удаление из системы уравнений, являющихся тождествами для всех х.

Пусть исходная система выглядит следующим образом

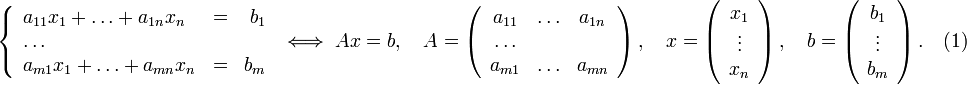
Матрица A называется основной матрицей системы, b — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

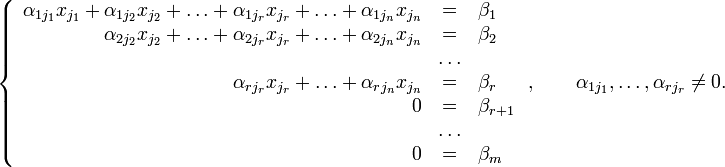
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных  ^[3].

Тогда переменные   называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число  , где i > r, то рассматриваемая система несовместна.

Пусть   для любых i > r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом   ( , где   — номер строки):

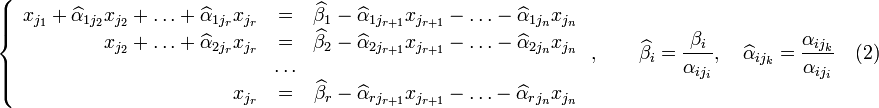, где 

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

56. Собственные значения и собственные векторы квадратной матрицы с действительными элементами.

Определение 10.2. Квадратная матрица называется симметрической, если  , то есть если равны элементы матрицы, симметричные относительно главной диагонали.

     Свойства собственных чисел и собственных векторов симметрической матрицы:

1)       Все собственные числа симметрической матрицы действительные.

Доказательство (для n = 2).

Пусть матрица А имеет вид: 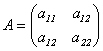 . Составим характеристическое уравнение:

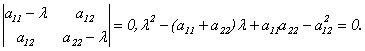                            (10.2)        Найдем дискриминант:

 следовательно, уравнение имеет только действительные корни.

2)       Собственные векторы симметрической матрицы ортогональны.

Доказательство (для n = 2).

Координаты собственных векторов   и   должны удовлетворять уравнениям:

 Следовательно, их можно задать так:

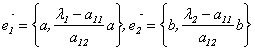. Скалярное произведение этих векторов имеет вид:

 По теореме Виета из уравнения (10.2) получим, что   Подставим эти соотношения в предыдущее равенство:   Значит,  .

 

Замечание. В примере, рассмотренном в лекции 9, были найдены собственные векторы симметрической матрицы и обращено внимание на то, что они оказались попарно ортогональными.

 

Определение 10.3. Матрицей квадратичной формы (10.1) называется симметрическая матрица 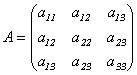  .                                              (10.3)

Таким образом, все собственные числа матрицы квадратичной формы действительны, а все собственные векторы ортогональны. Если все собственные числа различны, то из трех нормированных собственных векторов матрицы (10.3) можно построить базис в трехмерном пространстве. В этом базисе квадратичная форма будет иметь особый вид, не содержащий произведений переменных.

 

57. Алгебраическая форма комплексного числа. Арифметические операции над комплексными числами.

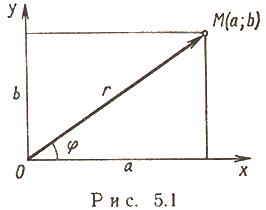
  Обозначения, терминология 

где i - мнимая единица; a - действительная часть: a = Re z; bi - мнимая часть: b = Im z; числа вида bi - чисто мнимые; плоскость Oxy - комплексная плоскость; ось Ох - действительная ось; ось Oy - мнимая ось;

       - число, сопряженное числу z = a + bi;

       - модуль комплексного числа;   либо  , - аргумент комплексного числа z (главное значение аргумента);

Arg z - множество аргументов числа z:

     Действия над комплексными числами 

     Если   то:

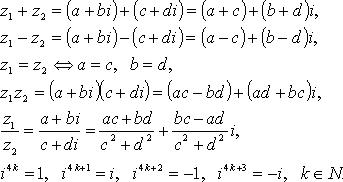
58. Тригонометрическая форма комплексного числа.

где r - модуль;   - агрумент комплексного числа.

     Если   то: