12. Линейная зависимость и линейная независимость векторов.

Линейной комбинацией n векторов a1, а2,..., an будем называть сумму произведений этих векторов на произвольные вещественные числа, т.е. выражение вида

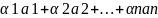
где а1, а2, ..., an — какие угодно вещественные числа.

Определение 1. Векторы а1 а2, ..., an называются линейно зависимыми, если найдутся такие вещественные числа а1 а2, ..., an, из которых хотя бы одно отлично от нуля, что линейная комбинация векторов а1 а2, ..., an с указанными числами обращается в нуль, т.е. имеет место равенство = 0

Векторы а1 а2, ..., an, не являющиеся линейно зависимыми, будем называть линейно независимыми.

Дадим другое определение линейно независимых векторов, основанное на логическом отрицании содержания определения 1.

Определение 2. Векторы а1 а2, ..., an называются линейно независимыми, если равенство нулю их линейной комбинации возможно лишь в случае, когда все числа 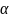1 2, ..., n равны нулю.

13. Линейные комбинации двух векторов.

14. Линейные комбинации трех и четырех векторов.

15. Понятие базиса. Аффинные координаты.

16. Проекция вектора на ось и её основные свойства.

17. Скалярное произведение двух векторов. Геометрические свойства скалярного произведения.

18. Скалярное произведение двух векторов. Алгебраические свойства скалярного произведения.

19. Скалярное произведение двух векторов в декартовой прямоугольной системе координат. Следствия.

20. Векторное произведение двух векторов. Геометрические свойства векторного произведения. Следствия.

21. Векторное произведение двух векторов. Алгебраические свойства векторного произведения. Следствия.

22. Векторное произведение двух векторов декартовых прямоугольных координатах. Следствия.

23. Смешанное произведение трех векторов. Геометрический смысл смешанного произведения.

24. Смешанное произведение трех векторов в декартовых прямоугольных координатах.

25. Вычисление определителя третьего порядка при помощи “правила треугольника”.

26. Двойное векторное произведение. Теорема о двойном векторном произведении.

27. Прямая на плоскости: общее уравнение прямой, неполные уравнения прямой.

28. Прямая на плоскости: уравнение прямой “в отрезках”, каноническое уравнение прямой.

29. Прямая на плоскости: уравнение прямой, проходящей через две различные точки, параметрические уравнения прямой.

См 28

30. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых, заданных общими уравнениями.

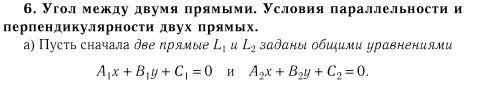
31. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых, заданных каноническими уравнениями.

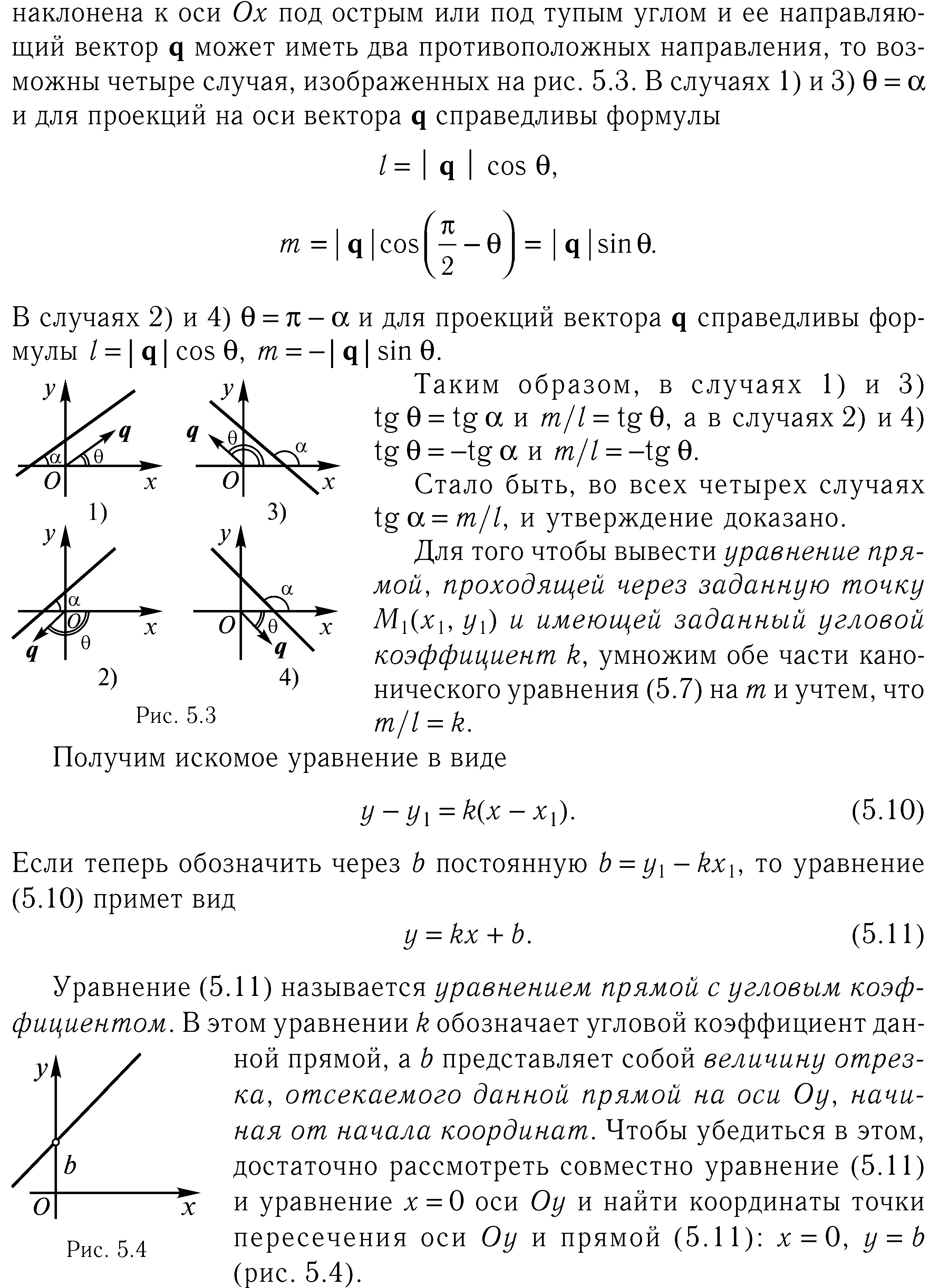
32. Уравнение прямой на плоскости с угловым коэффициентом, угол между двумя прямыми и условия параллельности и перпендикулярности прямых, заданных уравнениями с угловыми коэффициентами.

33. Нормированное уравнение прямой на плоскости, отклонение точки от прямой, нормирующий множитель.

34. Пучок прямых на плоскости. Теорема о пучке прямых на плоскости.

35. Некоторые задачи на прямую, расположенные на плоскости.

36. Правило Крамера для случаев, когда n=2 и n=3, где n-число неизвестных, m=n – число уравнений.

Системой однородных линейных уравнений называется система вида

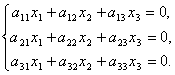
Ясно, что в этой случае  , т.к. все элементы одного из столбцов в этих определителях равны нулю.

Так как неизвестные находятся по формулам  , то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.

Теорема. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы Δ ≠ 0.

Итак, если определитель Δ ≠ 0, то система имеет единственное решение. Если же Δ ≠ 0, то система линейных однородных уравнений имеет бесконечное множество решений.