
- •Список вопросов, выносимый на экзамен, за 1 семестр
- •1. Параллельное и ортогональное проектирование.
- •2. Декартовы координаты на прямой.
- •3. Декартовы координаты на плоскости.
- •4. Декартовы координаты в пространстве.
- •5. Полярная система координат.
- •6. Цилиндрическая система координат.
- •7. Сферическая система координат.
- •9. Деление отрезка в данном отношении.
- •12. Линейная зависимость и линейная независимость векторов.
- •Примеры.
- •Линейные операции над матрицами.
- •Перемножение матриц.
- •Обратная матрица.
- •50. Ранг матрицы.
- •54. Система линейных однородных уравнений.
- •Доказательство
- •Определение 7.1
- •55. Эквивалентные системы уравнений. Элементарные преобразования уравнений системы. Метод Гаусса.
Перемножение матриц.
Выше было указано, что сложение матриц накладывает условия на размерности слагаемых. Умножение матрицы на матрицу тоже требует выполнения определенных условий для размерностей сомножителей, а именно: число столбцов первого множителя должно равняться числу строк второго.
Определение
3.6. Произведением
матрицы А размерности m
p и
матрицы В размерности ![]() называется
матрица С размерности
называется
матрица С размерности ![]() ,
каждый элемент которой
,
каждый элемент которой ![]() определяется
формулой:
определяется
формулой: ![]() Таким
образом, элемент
представляет
собой сумму произведений элементов i-й cтроки
матрицы А на соответствующие элементы j-го
столбца матрицы В.
Таким
образом, элемент
представляет
собой сумму произведений элементов i-й cтроки
матрицы А на соответствующие элементы j-го
столбца матрицы В.
49. Обратная матрица.
Обратная матрица.
Определение
3.7.
Квадратная матрица А называется вырожденной,
если ![]() ,
и невырожденной,
если
,
и невырожденной,
если ![]() .
.
Определение
3.8.
Квадратная матрица В называется обратной к
квадратной матрице А того же порядка,
если АВ
= ВА = Е.
При этом В обозначается ![]() .
.
Рассмотрим условие существования матрицы, обратной к данной, и способ ее вычисления.
Теорема 3.2. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.
Доказательство.
1) Необходимость:
так как ![]() то
то ![]() (теорема
3.1), поэтому
(теорема
3.1), поэтому ![]()
2) Достаточность: зададим матрицу в следующем виде:
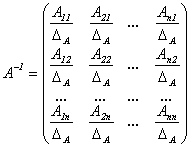 .
.
Тогда
любой элемент произведения ![]() (или
(или ![]() ),
не лежащий на главной диагонали, равен
сумме произведений элементов одной
строки (или столбца) матрицы А на
алгебраические дополнения к элементам
друго столбца и, следовательно, равен
0 (как определитель с двумя равными
столбцами). Элементы, стоящие на главной
диагонали, равны
),
не лежащий на главной диагонали, равен
сумме произведений элементов одной
строки (или столбца) матрицы А на
алгебраические дополнения к элементам
друго столбца и, следовательно, равен
0 (как определитель с двумя равными
столбцами). Элементы, стоящие на главной
диагонали, равны ![]() Таким
образом,
Таким
образом,
= .
Теорема доказана.
.
Теорема доказана.
Замечание. Сформулируем еще раз способ вычисления обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.
Пример.
Найдем
матрицу, обратную к 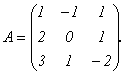
![]() следовательно,
матрица А невырожденная. Найдем
алгебраические дополнения к ее элементам:
следовательно,
матрица А невырожденная. Найдем
алгебраические дополнения к ее элементам:
![]() Не
забудем, что алгебраические дополнения
к элементам строки матрицы
А образуют в обратной матрице столбец с
тем же номером. Итак,
Не
забудем, что алгебраические дополнения
к элементам строки матрицы
А образуют в обратной матрице столбец с
тем же номером. Итак, 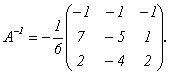 Можно
убедиться, что найденная матрица
действительно удовлетворяет
определению
Можно
убедиться, что найденная матрица
действительно удовлетворяет
определению ![]() Найдем
Найдем

Тот же результат получим и при перемножении в обратном порядке.
50. Ранг матрицы.
Для того что бы найти ранг матрицы можно использовать метод окаймления миноров. Суть его заключается в нахождении миноров, начиная с низших и двигаясь к более высоким порядкам. Если миноры более высоких порядков, например n+1 равны 0, при условии, что минор n-го порядка не равен 0, то ранг будет равен n.
На наш взгляд более простым является метод приведения матрицы к треугольному виду. И если в задании не указано, каким именно методом нужно искать, то предпочтительнее использовать именно данный способ. Наш онлайн калькулятор путем элементарных преобразований делает все элементы, стоящие ниже главной диагонали равными нулю. К элементарным преобразованиям относятся:
- перестановка двух параллельных рядов матрицы;
- умножение всех элементов какого-либо ряда на число отличное от нуля;
- прибавление ко всем элементам ряда соответствующих элементов параллельного ряда умноженных на одно и то же число.
Далее подсчитываем количество нулевых строк в матрице и отнимаем от общего числа строк. Полученное значение и будет рангом матрицы.
Для примера произведем расчет для матрицы 3×3
67 |
32 |
-2 |
-1.5 |
-1.4 |
10 |
14 |
12 |
5 |
На первом этапе отнимем первую строку от нижних, при этом добъемся что бы в первом столбце элементы начиная со второго стали равными нулю. Для этого умножим на -0.022 и 0.209. В итоге получим ниже приведенную матрицу.
67 |
32 |
-2 |
0 |
-0.684 |
9.955 |
0 |
5.313 |
5.418 |
Аналогичные действия проделаем со второй строкой. Умножим на -7.773
67 |
32 |
-2 |
0 |
-0.684 |
9.955 |
0 |
0 |
82.799 |
Так как количество нулевых строк равно нулю, а общее количество строк равно трем, то ранг матрицы равен: rang|A|=3-0=3
51. Элементарные преобразования матрицы.
Элементарными преобразованиями матрицы являются следующие преобразования:
умножение строки матрицы на число, отличное от нуля
прибавление к одной строке матрицы другой строки
перестановка строк между собой
вычеркивание (обнуление) одной из двух одинаковых строк
транспонирование матрицы.
Эти же операции, применяемые для столбцов матрицы, также являются элементарными преобразованиями. С помощью элементарных преобразований можно любой строке (или столбцу) матрицы прибавить линейную комбинацию остальных строк (или столбцов).
Элементарные преобразования не меняют ранга матрицы. Элементарные преобразования обратимы. Обозначение A ~ Bуказывает на то, что матрица A может быть получена из B путём элементарных преобразований (или наоборот).
52. Система линейных неоднородных уравнений (общий случай: m=n). Терема Кронекера-Капелли.
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
|
(1) |
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1].
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2). |
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называетсянеопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Теорема Кронекера-Капелли |
Для
того чтобы система m неоднородных
линейных уравнений с n неизвестными
была совместной, необходимо и достаточно,
чтобы Доказательство необходимости. Пусть система (1.13) совместна, то есть существуют такие числа х1=α1, х2=α2, …, хn=αn, что
Вычтем
из последнего столбца расширенной
матрицы
ранг
которой в результате элементарных
преобразований не изменится и Доказательство достаточности.
Пусть
Это означает, что остальные строки матрицы могут быть получены как линейные комбинации первых r строк, то есть m-r строк матрицы можно представить в виде сумм первых r строк, умноженных на некоторые числа. Но тогда первые r уравнений системы (1.13) самостоятельны, а остальные являются их следствиями, то есть решение системы первых r уравнений автоматически является решением остальных уравнений. Возможны два случая. 1. r=n. Тогда система, состоящая из первых r уравнений, имеет одинаковое число уравнений и неизвестных и совместна, причем решение ее единственно. 2. r<n. Возьмем первые r уравнений системы и оставим в левых частях этих уравнений первые r неизвестных, а остальные – перенесем вправо:
«Свободным» неизвестным xr+1, xr+2, …, xn можно придать какие угодно значения. Тогда соответствующие значения получают неизвестные x1, x2, …, xr. Система (1.13) и в этом случае совместная, но неопределенная. Замечание. Отличный от нуля минор порядка r, где r<n, будем называть базисным минором. Неизвестные х1, х2, …, хr так же называют базисными, остальные – свободными. Систему (1.16) называют укороченной. Если свободные неизвестные обозначить хr+1=c1, хr+2=c2, …, хn=cn-r, то базисные неизвестные будут от них зависеть, то есть решение системы m уравнений с n неизвестными будет иметь вид X = (x1(c1, …, cn-r), x2(c1, …, cn-r), …, xr(c1, …, cn-r), c1, c2, …, cn-r)T, где значок Т означает транспонирование. Такое решение системы называется общим. |
53. Система линейных неоднородных уравнений (общий случай: m=n). Правило Крамера. Метод обратной матрицы.
…
|

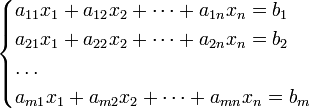
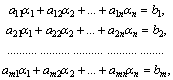 (1.15)
(1.15)

 (1.16)
(1.16)