- •Общая характеристика и обзор систем компьютерной математики*
- •Обзор возможностей системы Mathcad*
- •Концепции обработки документа в Mathcad*
- •Типы данных. Элементы входного языка Mathcad*
- •Выполнение базовых вычислений в MathCad, примеры
- •Работа с дискретными переменными в MathCad, примеры
- •Стандартные и пользовательские функции в MathCad, примеры
- •Обработка векторов и матриц в MathCad, примеры
- •Создание программных фрагментов в MathCad, примеры
- •Создание двумерных графиков в MathCad, графики кусочно-непрерывных функций
- •Редактирование и форматирование графиков в MathCad
- •Модуль 2. Численные методы
- •Численные методы решения уравнений*
- •Аппроксимация и интерполяция данных, основные определения*
- •Метод наименьших квадратов*
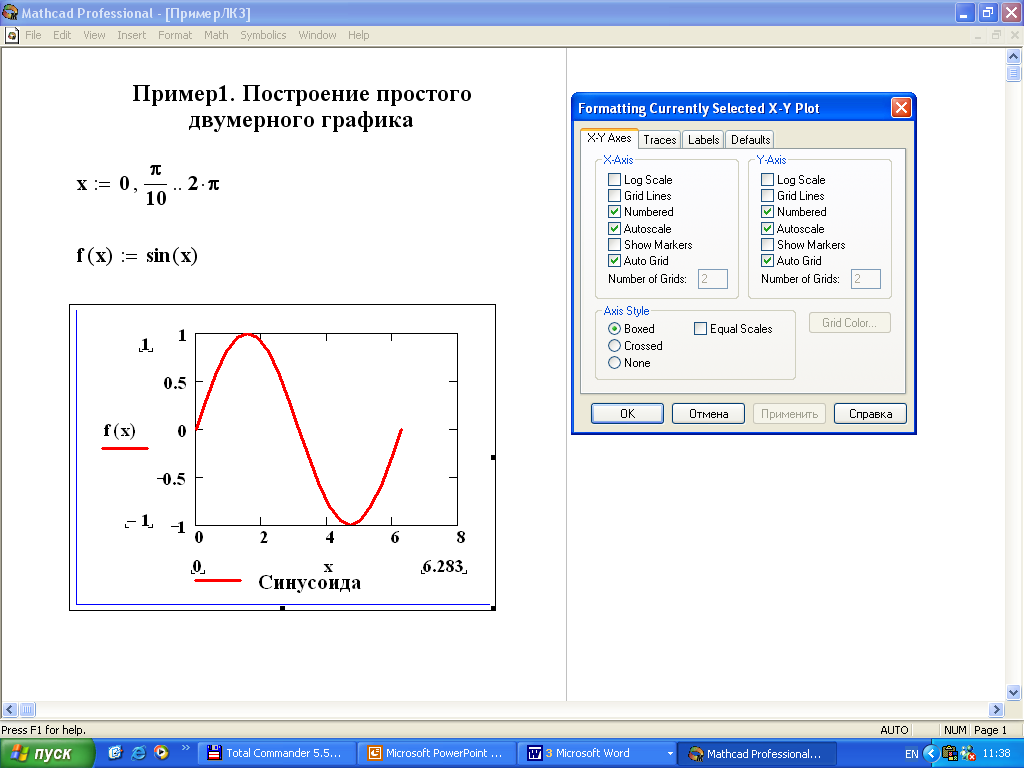
Создание двумерных графиков в MathCad, графики кусочно-непрерывных функций
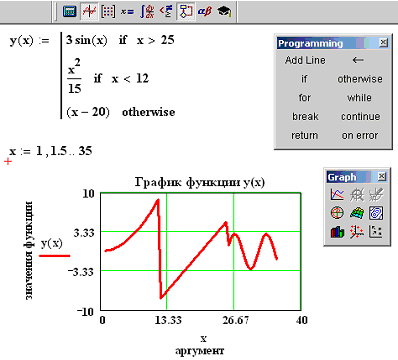
Редактирование и форматирование графиков в MathCad
|
Log Scale (Лог. масштаб) — установка логарифмического масштаба; Crid Lines (Линии сетки) — установка линий масштабной сетки; Numbered (Пронумеровать) — установка цифровых данных по осям; Autoscale (Автомасштаб) — автоматическое масштабирование графика; Show Markers (Нанести риски) — установка фоновых линий по осям; Auto Grid (Автосетка) — автоматическая установка масштабных линий; Nunber of Grids (Число интервалов) — установка заданного числа масштабных линий. Boxed (Рамка) — оси в виде прямоугольника; Crossed (Репер) — оси в виде креста; None (Ничего) — отсутствие осей;
|
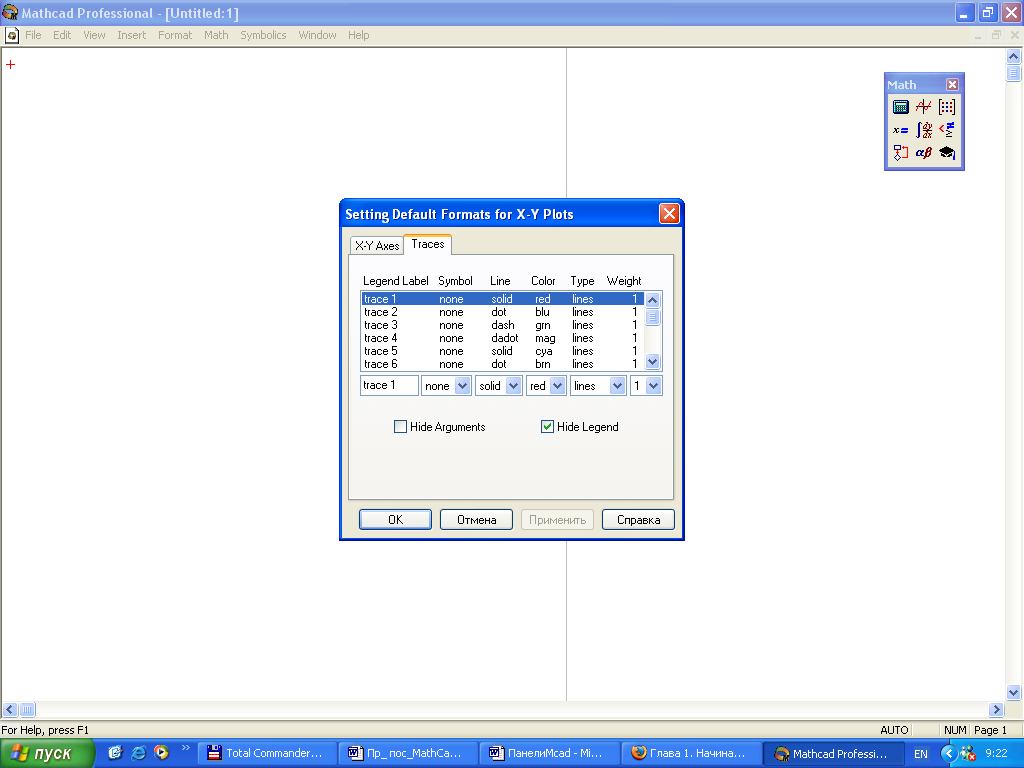
При форматировании линий графика выбирается закладка Traces в окне форматирования, вид окна форматирования линий приведен ниже.
|
Legend Label (Имя кривой) — указание названий линий в легенде графика; Symbol (Маркер) — установка символа отметки базовых точек графика; Line (Линия) — установка типа линий; Color (Цвет) — установка цвета линии и базовых точек; Type (Тип) — тип графиков; Weight (Толщина) — толщина линий. Hide Argument — скрываются обозначения математических выражений по осям графика; Hide Legend — скрываются обозначения имен кривых графика. |
Обработка внешних файлов в Mathcad
Символьные вычисления в MathCad
Модуль 2. Численные методы
Определение численных методов. Классификация численных методов*

Численные методы решения уравнений*
Метод простой итерации
В основе метода заложено понятие сжимающего отображения. Определим терминологию:
Говорят, что функция
![]() осуществляет
сжимающее отображение на
осуществляет
сжимающее отображение на
![]() ,
если
,
если
Тогда основная теорема будет выглядеть так:
|
Теорема Банаха (принцип сжимающих отображений). Если — сжимающее отображение на , то:
|
|
Поясним смысл
параметра
![]() .
Согласно теореме
Лагранжа имеем:
.
Согласно теореме
Лагранжа имеем:
![]()
Отсюда следует,
что
![]() .
Таким образом, для сходимости
метода достаточно, чтобы
.
Таким образом, для сходимости
метода достаточно, чтобы
![]()
.........
и так далее, пока
![]()
[править] Применительно к СЛАУ
Рассмотрим систему:
![]()
Для неё итерационное вычисление будет выглядеть так:

Сходимость
метода будет осуществлять
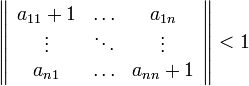
Следует отметить, что для оценки сходимости вычисляется не определитель матрицы, а норма матрицы. Поэтому в данном случае поставлены двойные вертикальные черты, а не одинарные.
[править] Алгоритм
Условие
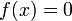 преобразуется
к виду
преобразуется
к виду
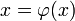 ,
где
,
где
 —
сжимающая
—
сжимающаяЗадаётся начальное приближение и точность
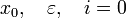
Вычисляется очередная итерация
Если , то
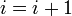 и
возврат к шагу 3.
и
возврат к шагу 3.Иначе
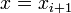 и
остановка.
и
остановка.
Численные методы решения систем уравнений*
Решения матричных уравнений.
Матричные уравнения решаются при помощи обратных матриц. Уравнение решается следующим образом. Пусть матрица А - невырожденная (D ? 0), тогда существует обратная матрица А-1. Умножив на нее обе части матричного уравнения, имеем А-1(АХ) = А-1В. Используя сочетательный закон умножения, перепишем это равенство в виде
(А-1А) Х = А-1В.
Поскольку А-1 А = Е и ЕХ = Х, находим:
Х = А-1В.
Такимобразом, чтобы решить матричное уравнение, нужно:
1. Найти обратную матрицу А-1.
2. Найти произведение обратной матрицы А-1 на матрицу столбец свободных членов В, т. е А-1В.
Пользуясь определением равных матриц, записать ответ.
При этом собственно нахождение обратной матрицы - процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому напрактике чаще применяют численные методы решения систем линейных уравнений.
К численным методам решения систем линейных уравнений относят такие как:метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над расширенной матрицей системы. А в методе Крамера - с определителями системы, образованными по специальному правилу.
Метод Крамера.
При решении систем линейных уравнений по методу Крамера последовательно выполняется следующий алгоритм:
1. Записывают систему в матричном виде (если это еще не сделано).
2. Вычисляют главный определитель системы:
3. Вычисляют все дополнительные определители системы:
4. Если главный определитель системы не равен нулю, то выполняют пункт 5. Иначе рассматривают вопрос о разрешимости данной системы (имеет бесчисленное множество решений или не имеет решений). Находят значения всех неизвестных по формулам Крамера для решения системы n линейных уравнений с n неизвестными, которые имеют вид:
Методы численного интегрирования*
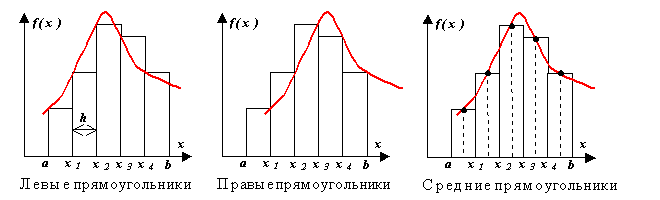
Метод прямоугольников.
Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.
Метод трапеций.
Аппроксимация в
этом методе осуществляется полиномом
первой степени. Суть метода ясна из
рисунка.

Метод Симпсона.
П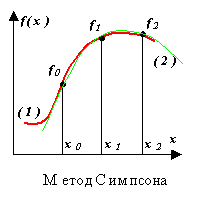 одынтегральная
функция f(x) заменяется интерполяционным
полиномом второй степени P(x) –
параболой, проходящей через три узла,
например, как показано на рисунке ((1) –
функция, (2) – полином).
одынтегральная
функция f(x) заменяется интерполяционным
полиномом второй степени P(x) –
параболой, проходящей через три узла,
например, как показано на рисунке ((1) –
функция, (2) – полином).