Простейшие типы точек покоя
Исследуем расположение траектории в окрестности точки покоя x=0
y=0
Система 2-ух линейных однородных уравнений с постоянными коэффициентами
(7.8)
0
Ищем решение в виде
x=
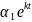y=
Для получения корней характеристического уравнения :
= 0
-
(
+
) k + (-
+
)
= 0
с точностью до постоянного множителя
определяемого из одного из уравнений
(7.9)
Рассмотрим следующие случаи :
Случай :
R ;
R
(7.10)
и
При k= и при k=
и произвольная постоянная
< 0 < 0
X=0 y=0
Асимптатично устойчивы
Так как точки лежащие в любой δ – окрестности начальные координаты при достаточно большом t переходе в точке лежащей в ε – окрестности начальной координаты
На рисунке (7.1) изображено расположение траектории для точки покоя данного типа – устойчивый узел.
Случай :
Траектории те же , направление другое
Точка покоя не устойчива, так как точки близкие к началу координат
0 0
Случай :
0 < 0
x=
y=
(7.11)
Однако существует движение приближенное к началу координат :
x=
y =
y=
x
Движение (7.11) проходит по прямой y= x
t ∞ t -∞
Точка покоя такого вида называется Седлом
Корни характеристического уравнения
= P
q
0
(7.12)
Здесь возникли следующие случаи
Случай 1) = P p<0 q 0
p<0
Второй множитель ограничен
p=0 - траекторией замкнутых кривых
(p<0)
Превращающееся замкнутые кривые в спирали асемптатично приближены к началу координат
Фокус отличается от узла тем, что касательные к траектории не стремятся ни к какому приделу при t ∞
Случай 2) = P p 0
q 0
Этот случай переходит в предыдущий при замене t на –t
Поэтому траектории те же но движение в другую сторону
Точка покоя не устойчива - не устойчивый фокус
Траектория – замкнутые кривые , содержащие внутри себя точку покоя называется центром рисунка (7.4)
Она устойчива, но асимптатичной устойчивости нету
Случай 3) : =
= < 0
x(t)
= (
+
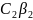t)
y(t)
= (
+
t)
Не исключена
возможность того , что
- произвольные константы
Точка покоя асемптатично устойчива так как 0
Точка покоя – узел
Устойчивый узел – дикритический узел
= 0
Замена t на -1 сводится к приводящему случаю только движения по траектории будут в противоположную сторону
Точки покоя - неустойчивый узел
Исчерпаны все возможности так как случай =0 исключают условия =0
=0
0
Решение (7.7) имеет вид :
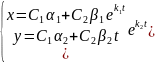
Получаем семейство параллельных прямых
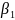(y-
)
=
(x-
)
0
При е стремящемуся к бесконечности движение происходит приближаясь к точке покоя
При
0
движение происходит в обратном
направлении и точка покоя x
y неустойчива
Случай 4)
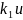=0
и
2)Общее решение имеет вид:
+ t
+
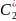t
и
линейная комбинация const
и
x
y