Случай :
корни характеристического уравнения действительны и различны
,
Є R
(i=
)
Один из коэффициентов может считаться = 1
Для
корня
системы частное решение :
:
=
*
=
=
:
=
*
=
=
:
=
*
=
=
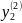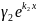
Можно показать, что эти функции создают фундаментальную систему :
=
+
+
=
+
+
=
+
+
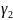Случай :
Корни характеристического уравнения различные и среди них есть комплексные
= a+ ib
= a- ib
R
+
+
x
+
=0
Вид частного решения в этой системе определяется также как и в случае 1
Замечание : вместо полученного частного решения можно взять их линейные комбинации
cos bx ,
sin bx
Корень a- i b не дает новых решений
Характеристическое уравнение имеет корень k ;
Кратность m (m =2,3)
а)
m=
2
= (A
+
)
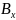= (C +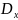
)
= (E +
)
m=3
= (A +
)
= (D +
)
= (G +
)
Это решение зависит от ’m’ производной постоянных A, B, C ,…, N определяемых методом неопределенного коэффициента
Выразить все коэффициенты через ’m’ полагается один из них равен 1, a остальные =0
Получится ’m’ линейно независимое частное решение системы (6.5)
§ 7 Понятие об устойчивости оду и систем оду Понятие о фразовом пространстве ду
В Евклидовом пространстве с прямоугольными координатами … решение системы :
= (t) = (t)
= (t, ,…, ) (i=1 , .., n) (7.1)
скорость
точки
;
…
При интегрировании (7.1)
= F
(t,
x)
(7.1a)
Динамическая система (7.1) определенная в заданный момент времени t в пространстве ,…, поле скоростей
Если векторно – функциональная зависимость явно то t векторные траектории могут не пересекаться
Если f не зависит от t , то поле скоростей стационарно.
Рассмотрим t как параметр полученный на фазе имеющей семейство окружностей с центром в начале координат
= F(t, x) (7.1a)
Фиксируя получим определенную траекторию
Причем различные присущи различным движениям
Фаза траектории состоит из 1 точки О которая называется точкой покоя (7.2)
Устойчивость по Ляпунову
При математическом описании различных процессов происходит некоторое округление , так как мы не учитываем факторы незначительно влияющие на процесс.
Возможно, что не учитываемые факторы сильно влияют на процесс, меняя его количественную и качественную характеристику
Во многих случаях можно указывать условия, при которых упрощение не возможно
Пусть некоторое явления описываются системой ДУ :
=
( t,
)
(
)
=
o
(i=
)
(7.3)
Если
решение
не
только устойчивое но и удовлетворяет
условию:
lim
│
(t)
-
=0
(7.5)
t
∞
│
(
)
-
│
<
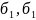>0
- асимптатичная
устойчивость
Заметим
, что из условия (7.5) не следуете
устойчивость решения
=
)
Из устойчивости решения не следует- его асимптатичности
Исследование на устойчивость решения системы (7.3) может быть сведено к исследованию на устойчивость тривиального решения
Тогда система (7.3)
=
(t)
(i
=
=
(t)
(i
=
(7.6)
=
+
(t,
+
(t),
+
,…,
+
(t))
(7.7)
Решение = (t) уравнения (7.7), которое мы исследовали на устойчивости в силу замены = - I (t) соответствует тривиальному решению (7.7)
Поэтому мы будем исследовать на устойчивости точку покоя, расположенную в начале координат.
Условия устойчивости точки покоя : =0 (i= )
Устойчивость в смысле Ляпунова если для каждой ε 0 можно подобрать δ; (ε) такое, что
То
есть траектория начальная точка
которой находится в точке
окрестности начальной координаты при
t
T
не выходит за пределы ε – окрестности
начальной координаты.