§ 3 Линейные обыкновенные дифференциальные уравнения
ЛОДУ п-го порядка – уравнение линейной относительности неизвестной функции и её производной и значит имеющий вид:
+
(x)
+ … +
(x) *
+
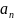(x) y= ϕ (x) (3.1)
Если правая ϕ (x)≡0 то уравнение называется линейным однородным
Поскольку , однородно относится неизвестная функция y и её y’
Если
коэффициент
ни в одной точке некоторого отрезка
a
то разделим на
приведем к виду
+
(x)
+ … +
(x) y’ +
(x) y = 0 (3.2)
=-
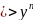Лоду 2-го порядка
Рассмотрим линейное дифференциальное уравнение 2-го порядка
+
(x)
y’
+
(x)
y
0 (3.3)
Решения
Устанавливается некоторыми свойствами его решения
Теорема :
Если функции = (x)
=
(x)
являются частными решениями (3.3) то решение этого уравнения является функция
y=
(x) +
(x) (3.4)
= const
= const
Подставляем
функцию y=
(x)
+
(x)
’
+
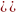(x)
)
=
+
(x)
+
(x)
+
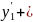
(x)
+
(x)
=
(
)
+
(
+
(x)
+
(x)
=
= 0 +0=0
решение уравнения (3.3)
и – решение уравнения (3.3)
Т.
О. функция y=
– является решением (3.3)
функция (3.4) содержит произвольную const : и
Но не непонятное является ли это общим решением
Введем
понятие линейной
зависимая функции:
функция
и
называется линио независимой на
интервале (a
;b)
если равенство
+
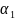= 0 (3.5)
и
– некоторые числа
Выполняется тогда когда = =0
Если хоть одно из чисел или отлично от нуля и выполнится равенство (3.5) , то функция и называется линейно зависимыми
Функция и линейно зависима только тогда, когда их отношение = const
= с = const
R
Например : = =3
=
=
= const
линейно зависима
Функция
=
и
=
= ≠ const линейно независима
Определить является ли данная формула линейно зависима можно с помощью определителя Вронского
Для 2-ух
дифференциальных функций
вронскиан имеет вид:
w
(x)
=
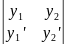
Теорема 3.2 : Если дифференциальная функция (x) и (x)
Линейно зависима на интервале от a до b то определитель Вронского на этом интервале = 0
Доказательство :
Поскольку
+
= 0 либо
0
=и -
Поэтому
для
w
(x) =
= 0
Теорема 3.3 :
Если функции (x) и (x) линейно независимы решения уравнения (3.3) на (a ;b) , то определитель Вронского не обращается в ноль
Из (3.2) и
(3.3) следует, что Вронскиан не равен
0 ни в одной точке от (a
;b)
, тогда когда частное решение линейно
не зависимо
Совокупность
2-ух
линейно не зависимых на (a
;b)
частных решений :
(x) , (x)
ЛОДУ 2-го порядка определяет фундаментальную систему решений уравнений
решение можно получить как комбинацию y= (x) + (x)
Теорема 3.4 :
Если 2 частных решения (x) и (x) ЛОДУ (3.3) образуют фундаментальную систему на (a ;b) то общее решение этого уравнения является :
Функция = (3.6)
и - произвольная постоянная
Доказательство :
По теореме (3.1) функция (3.6) является решением уравнения (3.3) можно доказать, что это решение общее, то есть что из него можно получить единственное частное решение удовлетворяющее условию :
y (
y’
(
(3.7)
Подставим в условие (3.7) решение (3.6) получим систему :
y ( , y’ (
=
(
+
(
=
(
+
(
= W (
Так как
решение (y.1)
и (y.2)
образует фундаментальную систему
решений и
(a
,b)
то по теореме (3.3)
W ( 0
по этому система уравнения имеет единственное решение :
=
=
=
=
y = + (единственная в силу теоремы единственности)
Уравнение (3.3) удовлетворяет начальным условия (3.7)
На основе теоремы (3.40 общее решение уравнения y’’+y=0
Является функция y= sinx+ cosx
Линейно однородные дифференциальные уравнения n-го порядка
Полученный результат можно обобщить на ЛОДУ n- го порядка , имеет вид :
+
(x)
+
(x)
+ … +
(x) y = 0 (3.8)
Если функция
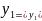(x)
,
(x)
…
(x)
является частным решением уравнением
(3.8) , то и функция
y
+ … +
- является его решением
Функции
называется линейно не зависимыми на
(a
;b)
, если равенство :
+
+ ….. +
= 0
Выполняется
если все
=0 (i = 1 ,
)
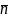В противном
случае функция
линейно зависима
Определитель Вронского имеет вид :
W(x)
=
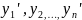
Частный случай решения
уравнение (3.8) образует фундаментальную
систему , если :
W (x) 0 , x (a ; b)
Общее решение ЛОДУ (3.8) имеет вид: y +
+
где
,
- образующаяся фундаментальная
система решения