§8 Уравнения в частных производных Основные понятия
Дифференциальные уравнения с частными производными – дифференциальные уравнения , в которых неизвестная функция зависит более чем от одной переменной
Многие физические явления описываются дифференциальными уравнениями с частными производными
Например :
+
+
= n (x, y,
z) - описание распространения
светового луча в неоднородной среде с
показателем преломления
n (x, y, z)
Уравнение
=
- 2 порядок
Описывает температуру плавления стержня
=
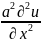- 2 порядок
Явление колебания струны
Уравнение Лапласа
+
+
= 0
Удовлетворяет потенциалу поля в области не содержащей заряд поля
Линейные и Квазилинейные уравнения частных производных
Линейные неоднородные уравнения или квазилинейные уравнения первого порядка в частных производных называется уравнение вида
(
+
(
+
(
= z(
(8.1)
Это уравнение линейное относительно производной но может быть изменено относительно не известной z.
Если правая часть 0 а коэффициент не зависит от z , то уравнение (8.1) называется линейно однородным
Рассмотрим более подробно квазилинейные уравнения с 2-умя независимыми переменными
P
(x, y, z)
+ Q (x, y, z)
= R (x, y, z) (8.1a)
Функцию P, Q, R будем считать не прерывной в рассматриваемой области изменённой переменой и не обращающейся в ноль одновременно
Рассмотрим
непрерывное поле
:
=
P
(x,
y,
z)
+ Q
(x,
y,
z)
1 + n
(x,
y,
x)
Векторные линии поля , то есть линии, касательно которых в каждой точке имеют направления
=
dx +
dy +
dz ,
-
=
Поверхность целиком содержащая векторные линии, или хотя бы одну общую точку с поверхностью называется векторной поверхностью
Векторные
поверхности характерны тем, что вектор
направлен по нормали к поверхности.
В
точке поверхность ортогональна полю
,
то есть :
( * ) =0 (8.2)
Если векторная поверхность
+ -
и условие (8.2) принимает вид :
P (x, y, z) * + Q (x, y, z) = R (x, y, z) (8.3)
Если векторная поверхность задаётся:
U (x, y, z) = 0
+
-
И уравнение (8.2) приобретает вид :
P
(x,
y,
z)
*
+ Q
(x,
y,
z)
+ R
(x,
y,
z)
= (8.4)
Так как векторные поверхности могут быть составлены из векторных линий
То интегрирование уравнения (8.3) или (8.4) сводиться к интегрированию системы обыкновенных дифференциальных уравнений векторных линий
Составим систему дифференциальных уравнений векторных линий :
- = (8.5)
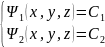
из 2-ух параметрических
семейств векторных линий
Называется характеристиками уравнения (8.3) или (8.4) произвольным способом параметрического семейства
Устанавливая какую – нибудь зависимость Ф ( ) = 0 тогда параллелограмм и
Исключение из системы :
Ф- произвольная функция (непрерывная)
Найдем интеграл квадратного уравнения (8.3) зависящего от произвольной функции
Если требуется найти не произвольный вектор поверхностного поля
= P (x, y, z) + Q (x, y, z) + R (x, y, z)
А поверхностный проход через заданную линию определяется уравнением
То функция (8.6) уже не будет произвольной , определяемая присутствием исключений x, y, z из системы
(x, y, z) =
(x, y, z) =
Которые должны одновременно удовлетворять в задней линии =0 , =0
Через которую мы проводим характеристики определяемые уравнениями :
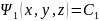
Заметим, что задание станет неопределяемым если задание меньше (x, y, z) = 0
(x, y, z) = 0 является характеристикой , т.к. в этом случае эту линию можно включить в различные однопараметрические семейства характерные тем самым получим различные интегралы появляющееся через эту линию.
Система дифференциальных уравнений с частными производными 1-го порядка
Во многих областях науки встречаются системы величин, которые связаны между собой не одним, а сразу несколькими соотношениями , рассматривается задача Коши для систем из двух уравнений с двумя начальными условиями
+ 8
=0
+ 2
=0
∞ < x < +∞
0 < t < ∞
(x,
0) = f(x)
(x,
0) = d(x)
Эта задача может соответствовать определению давления и плотности , как формула u пространствует координатам x и времени t
(x, 0) = f(x) - давление
(x, 0) = d(x) - плотность
x - координат
t – время
Запишем систему уравнений в матричной форме
+
=
+ A
=
(8.7)
A =
=
=
=
Введение новой неизвестной функции v = с помощью преобразования u = pv , где p- матрица , по столбцам которой стоят собственные векторы матрицы А.
Собственные числа матрицы А являются корнями уравнения :
det (A – λ E)=0
или
= 0
– 16 = 0
= 4
= - 4
Найдём собственный вектор соответствующий собственному значению = 4 из системы
(A – E) ( ) = 0
=
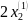
=1
=2 =>
P=
= - 4
=
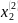= 1,
= - 2
P=
*
=
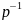
det p= 4
AP
=
=
=
= B
Оказалось,
что после замены переменных по формуле
u=pv
для определения v
получится очередная простая система
2 уравнения относительно новых
, после того по формуле pv
находится искомая формула
но сначала вычислим, как выглядит
система для определения v
продифференцируем обе части соотношения
u=pv
получаем :
= p
= p
(8.8)
Теперь подставим соотношения (8.8) в системе :
+ A = 0
+ A│
= 0 │*
+
A
=0
+ B
=
0 (8.9)
Раньше мы уже видели , что B
Заменим (8.9) в развернутой форме :
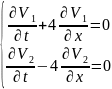(8.10)
Получилась система из 2х не связанных уравнений которые решаются независимо их решениями будут :
=
x- 4t =
= ϕ (x-4t)
:
=
x-+4t =
= ϕ (x+4t)
Для получения общего решения нужно выполнить по формуле : u=pv
= =
(x, t) =
(x, t) =
Решается задание Коши :
│2
Φ(x) = (f(x)+2y(x))
Ψ(x)= (2f(x)- f(x)) =>
Ответ :
(x, t) =
(f(x-4t)+2y(x-4t))-
(2y(x+4t)-f(x+4t))
(x, t) = (2y(x-4t)-f(x-4t)+ (2d(x+4t)-f(x+4t))
Замечание : часто численные методы ориентируются на решение систем уравнений , а значит многие программы для компьютера написаны так чтобы решить систему уравнений первого порядка, поэтому приходится преобразовывать свое уравнение высшего порядка в систему первого порядка.