§ 2 Дифференциальное уравнение 1-го порядка

Обыкновенное дифференциальное уравнение 1-го порядка первой степени можно разрешить относительно к производной представляя в виде (1.7). Простейший пример такого уравнения:

= 1(х)

В этом случае:

y=

Содержит произвольную постоянную, которая может быть определенна если известно первоначальное значение:

y( ) =

Тогда y= +

Вообще при некотором ограничении на функцию f(x)=y уравнение:

= f (x, y)

также имеет одинаковое решение удовлетворяющее условию :

y ( ) =

а его общее решение зависит от одной произвольной постоянной

Уравнение с раздельной переменой

Дифференциальное уравнение вида:

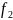(y) d y= (x) dx (2.1)

называется уравнением с раздельными переменными

Функции (x) и (y) будем считать непрерывными, если y – решение, то после подстановки его в (2.1) и интегрируя, получим:

Уравнение (2.2)и (2.1) – равносильны

Может получиться так, что интегралы нельзя выразить в элементарной функции. Однако, в этом случаи мы будем считать задачу интегрирования дифференциального уравнения (2.1) выполненной, поскольку мы сведём её к нахождению данного неопределенного интеграла (квадратуры) .

Если надо выделить частное решение, удовлетворяющее условия:

y = (

то оно очевидно определяется уравнением:

=

которое получится из:

= + С

Воспользовавшись начальными условиями: y = (

Уравнение вида:

В котором коэффициент при дифференциале распадается на множители зависимые только от x и от y , называется дифференциальным уравнением с разделёнными переменными и после деления на:

приводит к уравнению с разделенными переменными

dx = dy

При деление на (y) * (x) могут потеряться частные решения, обращающие в ноль произведение (y) * (x)

Уравнения , приводящее к уравнениям с разделенными переменными

Некоторое уравнение путем замены переменных можно подвести к уравнению с разделенными переменными.

a и b –постоянные числа , которые заменой:

z = ax + by

приводят к уравнению с разделенными переменными

f (x)

= dx

x = + C

Пример : = 2k + y

z = 2x + y

= 2 + z

= dx

Ln (z + 2) = x + C

z = - 2 + e ˄

2 x + y = -2 +

y = -2 -2x +

К уравнению с разделёнными переменными приводит и однородное дифференциальное уравнение 1-го порядка:

= f ( )

z = y = x z

x =

Напомним , что функция ϕ (x , y) называется однородной степени k

4 (tx , ty ) = ϕ (x , y)

Правая часть однородного уравнения , является однородной функцией переменных x и y нулевой степени однородности.

Поэтому уравнение вида :

M (x, y) dx + N (x , y) dy = 0

Будет однородным если M (x , y) и N (x , y) является однородной функцией (x , y) одинаковой степени однородности, то есть в этом случае

Уравнение такого вида преобразуется в однородное уравнение путем переноса из начала координат в точку пересечения ( ) переменных

Действия в новых координатах

x = x -

y = y -

Свободный член = 0

Коэффициент при текущей координате остается неизменным , а производная :

и уравнение (2.3) преобразится к виду:

)

или ) = ϕ (

и является Однородным Уравнением

Этот метод не применим если эти прямые:

x + 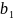y + = 0 - параллельные

x + y + = 0

на = c

= k

И уравнение (2.3) может быть записано в виде : f (

которое с заменой

z = , преобразованное уравнение в уравнении с разделом переменной .

Линейные Уравнения 1-го порядка.

Линейные Дифференциальные Уравнения 1-го порядка -линейное уравнение относительно неизвестной функции и её производной

Линейное уравнение имеет вид :

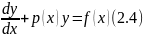
Где p(x) и f (x) непрерывное функции от x в той области в которой требуется проинтегрировать уравнение (2.4)

Если f(x) ≡ 0 , то уравнение (2.4) – линейное однородное

В линейном однородном уравнении:

Интегрируя получим :

ln │y│ = > 0

y = C e -

при делении на y мы потеряем решение y=0. Однако его можно включить в общее решение (2.5) позволив C=0

Для интегрирования неоднородного линейного уравнения (2.4) может быть применен метод вариации произвольного постоянной (М . Лагранжа) :

Интегрируя однородное уравнение, его решение имеет вид (2.5) ;

потом чтобы найти общее решение (2.4) , позволим константе C быть функцией f (x) , то есть

y = C (x) C (x) p(x) *

и подставляем в исходное неоднородное уравнения (2.4)

* -C (x) p (x) + p(x) C (x) = f(x)

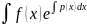C (x) = * dx

y (x) = * * dx (2.6)

В конкретном случае не целесообразно пользоваться формулой (2.6)

А нужно делать вычисления по Методу Лагранжа

Ищем решение по Методу Лагранжа

C(x) =

Ответ: y=( 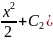* x

Множества дифференциальных уравнений могут быть сведены к линейным

Например уравнение Бернулли :

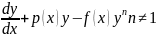
Замена :

Z =

Дифференцируя получим :

(1 – n )

и подставляя в (2.7) получим линейное уравнение

+ p (x) z = f (x)

Уравнение Риккати

В общем случае не интегрированно в квадратурах

Однако если известно одно частное решение , то уравнение Риккати можно свести к уравнению Бернулли

Для этого положим сделаем замену:

y =

+ p(x) + p (x) z + q (x) * + q (x) * 2 z + q (x) = f (x)

+ p(x) z + 2q (x) z +q(x) = 0

+z (p (x) + 2q (x) ) + q (x) =0

n=2 Бернули