Интегрирование лнду п-го порядка (n постоянным коэффициентом и правой частью специального вида
Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка
+
(x)
+
(x)
+ … +
(x)y
=
(x)
, …,
(x)
, f(x)
, x
(а, в) = f(x)
+ (x) + … + (x)y = 0
Теорема (5.3) : ( О структуре общего решения ЛНДУ n-го порядка)
Общее решение y ЛНДУ n-го порядка = сумме частного решения НУ и общего решения ОУ
y=
может быть найдено если известно общее решение ОУ
=
+
+ … +
y(x) – частное решение образующее фундаментальную систему решений ОУ
+
+ … +
= 0
+
+ … +
= 0
+
+ … +
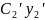= 0
+
+ … +
= f (x)
Однако для ЛНДУ n-го порядка с постоянными коэффициентами , правая часть f(x) которая имеет специальный вид, можно найти методом неопределенных коэффициентов
Метод подбора частного решения для уравнения :
y’’ + + … + y = f (x) R
§6 Системы дифференциального уравнения
Основные понятия
Для решения многих задач в математике , физике , техники , биологии не редко требуется несколько функций
Нахождение этих функций может привести к нескольким дифференциальным уравнениям образующих систему
Системой ДУ – называется совокупность дифференциальных уравнений, каждое из которых содержит независимые непеременные, искомые функции и их производные
Общий вид системы ДУ 1-го порядка содержат n искомых функций :
Система ДУ 1-го порядка решают относительно производных, то есть система вида :
=
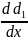(x,
)
=
(x,
)
Число уравнений = числу искомых функций
Часто система уравнения и система уравнения высшего порядка можно привести к нормальным системам вида (6.1)
Уравнение 3- го порядка
y’’’ = f ( x , y , y’ , y’’)
Путем замены : y’ = p y’’ = q
Решение системы (6.1) называется совокупностью из n функций :
удовлетворяет каждому уравнению из этой системы
Вначале условия для (6.1) имеют вид:
(
)
=
(
)
=
….. ,
(
)
=
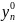(6.2)
Задача Коши для (6.1) :
Нужно найти решение системы (6.1) удовлетворяющее условию (6.2)
Условия существования и единственности решения задач Коши с формулирована в § 3.3 (т 3.6)
Общее решение (6.1) имеет вид :
=
(x,
)
=
(x,
)
Решение получившиеся
из общего из конкретного значения
const
…
называются частными решениями
системы (6.1)
Интегрирование нормальной системы
Одним из основных методов интегрирования нормальной системы ДУ является метод сведения к одному ДУ высшего порядка
Он основывается на следующих положениях :
Возьмем из (6.1) 1-ое уравнение и продифференцируем:
=
+
*
+ … +
*
Подставим значение производной :
,
, … ,
+
+…+
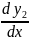Продифференцируем это равенство еще раз и заменив их производную выразим систему (6.1)
=
+
*
+…+
*
=
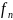
(x,
,…,
)
Соберем полученное уравнение в системе :
= (x, , ,… )
=
(x,
,
…
)
(6.3)
=
(x,
,
,…
)
Из первых (n- 1) - го уравнений системы (6.3) выразим функцию
,
,…
Через x :
x,
…
=
(x,
,
’,
…
)
=
(x,
,
’,
…
)
(6.4)
Найдем значение … подставим в n-ое уравнение (6.3) и получим уравнение n-го порядка
= φ(
x,
,
’,
…
)
= (x, … )
Продифференцируем (n – 1) раз и подставим значения производных
’,…,
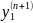в уравнении (6.4)
Найдем функцию :
= (x, … )
= (x, … )
Замечание : система уравнения (6.1) можно решить методом интегрируемых комбинаций
Суть метода : что выполняемые арифметические операции над уравнением получить легко интегрированные уравнения относительно новых переменных
Система ЛДУ с постоянными коэффициентами
Рассмотрим еще 1 метод интегрирования системы (6.1) в случае когда она представлена системой линейного ДУ с носителем коэффициента , то есть :
=
=
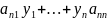
При y=3
=
=
=
j (i, j=
)
= const
=
α
=
β
=
γ
(6.6)
α ,β ,γ, k – const , который надо подобрать так , чтобы функция (6.6) удовлетворяла (6.5)
Подставим (6.6) в (6.5)
αk
=
α
+
β
+
γ
βk
=
α
+
β
+
γ
γk
=
α
+
β
+
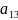γ
α ( -k) + β + γ =0
α+ β( -k) + γ =0
α + β + ( -k) γ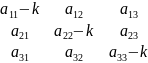=0
=0
Уравнение (6.8) - характеристическое уравнение (6.5)
Раскрыв определитель получим уравнение 3 степени относительно к :
Возможны 3 случая :