2.5 Уравнение в полных дифференциалах

d U = 0

U = C

U (x , y) = C

Может быть , что часть уравнения :

M (x , y) dx + N(x , y ) dy = 0 (2.8)

является полным дифференциалом некоторой функции U (x, y)

d U (x, y) = M (x, y) dx + N (x , y) d y => уравнение (2.8) принимает вид:

d U (x , y) = 0

Если функция y(x) является решением уравнения (2.8) тогда dU (x, y(x)) ≡ 0

U (x, y(x))= c (2.9)

C= const

Если некоторая функция y(x) обращается в тождественное уравнение (2.9) , то дифференциал=0 и наоборот :

d U (x, y (x)) = 0

U (x, y) = C

Для того чтобы левая часть уравнения (2.8) является полным дифференциалом некоторой функции от (x , y) , как известно необходимо условие Эйлера

(2.10)

Если условие Эйлера выполняется, то уравнения (2.8) легко интегрировать

Дифференцируем d U = M d x + N d y

d U=

При вычитание интеграла величина у рассматривается как const

Поэтому c(y) является произвольной функцией y

Для определения C(y) дифференцируем найденную функцию U(x, y) по y

Получим : (

В некотором случае ,когда левая часть (2.8) не является полной дифференциалом, легко удается подобрать функцию умножения на которую, левая часть (2,8) превращается в полный дифференциал то есть :

d U = ϻM dx + ϻN dy

Такая функция ϻ– интегрируемая множеством ϻ(x, y) может привести к появлению постороннего решения , обращающего (x, y) в ноль

Надо подобрать ненулевое решение уравнения:

(2.11)

Вообще задача интегрирования (2.11) ничем нелегче (2.10)

Если считать ϻ – Ф одной переменной будь то x, y, … , то задача упрощается

Например : условие, когда ϻ (x) => - непрерывная функция x =>

Ln M =

M= C * (2.12)

Можно считать c=1, так как нам нужен хоть 1 интегральный множитель

Если 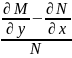является функцией тока x то интегральное множество найдется по уравнению (2.12)

Аналогично можно выписать условия при которых интегральное множество зависит от другой выбранной переменной

Уравнение Лагранжа

Уравнение Клеро

y=x ϕ (y’) + Ψ (y’)

Дифференцируем по x

y’ = p получим :

P= ϕ (P) + x ϕ’ (p) * (2.13) [P- ϕ(p)]

Линейное уравнение относительно x 4

Легко интегрировать методом вариации произвольной постоянной

Получим интеграл

φ ( x, p, c)=0

Уравнение (2.14) и присоединяя к нему y=x ϕ (p)+Ψ (p) получиv уравнение определяемое исполнимые кривые

При делении на , мы потеряем решение, для которого p- const =>

Если p= const ,(2.13) удовлетворяет в случае , если p –ϕ (p) = 0

Отдельно надо рассматривать случаи когда p-ϕ(p)=0 и следовательно при делении на теряется решения p=c , где c – искомое решение

ϕ (y’)≡y’

y= y ϕ (y’)+ Ψ (y’)

y= / y ‘ + Ψ (y’)

Уравнение Клеро

Делаем замену

y’=p

y= xp + Ψ (p)

Дифференцируем по x :

y’= p+ x

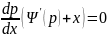
X+Ψ’ (p) = 0

В первом случае :

y=cx + Ψ(c) (2.15) - однопараметрическое семейство интегриральных прямых

В втором случае :

y=cx + Ψ(c) (2.15)

y= xp + Ψ(p) (2.16)

x+ Ψ’ (p)=0

Интегральная кривая, определенная уравнением (2.16) является огибающей семетр. прямых (2.15)

Теорема : ( Существование и Единство решения)

Уравнение

Со времен Эйлера дифференциальное уравнение приближённо решаются численными методами.

Это связанно с тем , что лишь немногие уравнения интегрируются в квадратурах.

Однако для численного решения нужно быть уверенным в существовании решения и его единственности

Для уравнения достаточно условий существования и единственного решения даны в следствие теореме

Теорема 2.1:

Пусть в уравнении (2.17) функция f(x, y) – непрерывна в прямоугольной области D

D: – a x +a

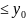– b y +b

И удовлетворяет условия Липшица:

– f ( 1

Где N= const

y=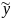 (x)

- H +H

Удовлетворяет условию y ( )=

Где H< min из таких чисел (a; ; )

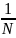M – max f (x, y) в D