Дифференциальные и интегральные уравнения

§ 1 Общие понятия

При изучении химии, физики, экологии часто возникает уравнения связывающие неизвестную функцию и ее производные. Такие уравнения называются дифференциальными уравнениями.

1. dx/dt=-kx—уравнение радиоактивного распада, где k-постоянная распада,

x-количество неразложившегося вещества в момент времени t

Скорость распада dx/dt пропорц. количеству нераспавшегося вещества.

2)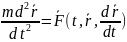 —Уравнение движения точки массой m под действием силы F

Сила равна произведению массы на ускорение.

3)

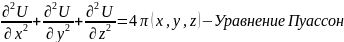
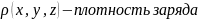
Нахождение неизвестной функции, определенной дифференциальным уравнением, является основной теории дифференциальных уравнений. Если в дифференциальном уравнении неизвестная функция является функция одной переменной, то дифференциальное уравнение называется обыкновенным(ур. 1)и2)). Если неизвестная функция зависит от двух переменных, то уравнение называется уравнением частных производных(ур.(3)).Порядок дифференциального уравнения называется максимальный порядок, входящий в уравнении производной неизвестной функции. Решением дифференциального уравнения называется функция, которая при постановке в дифференциальное уравнение, обращает его в тождество.

Например уравнение радиоактивного распада :

dx/dt=-kx (1.1)

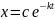(1.2) где c- произвольная постоянная

Уравнение (1.1) не вполне определяет закон распада x=x(t).

Нужно также знать количество вещества x(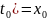 в момент времени

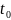
Тогда закон Распада примет вид:

x=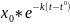

Процесс нахождения решений дифференциального уравнения, называется интегрированием дифференциального уравнения. Не всегда решение находится в явном виде.

При использовании ПО можно решить дифференциальное уравнение приближено с большой плотностью.

Пусть математическая точка движения под действием силы F:

Уравнение Движения : m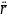 = F(t, 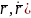(1,3)

Для нахождения закона движения 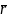(t) необходимо знать начальное положение точки и скорость:

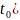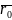( = (1.4)

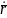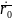( ) = (1.5)

При (1.4) и (1.5) называется Задачей Коши

Вектор уравнения 2-ого порядка (1.3) можно переписать в виде системы 2-ух векторных уравнений 1-го порядка, если рассмотреть скорость v как вторую неизвестную формулу:

=

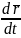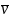
= F (t, , ) (1.6)

Каждое векторное уравнение в трёхмерном пространстве может быть заменено системой из 3-х векторов на оси координат. При интегрировании дифференциального уравнения обычно ставят цель найти все его решения. Например : в уравнение (1.1) все решения получены из решения (1.2) при некотором выборе постоянного C . Решение (1.2) – общее решение уравнения (1.1)

Решение дифференциального уравнения, получившегося из общего решения называется частным. Однако иногда не удаётся включить в общее решение все решения уравнений. Решения не являющееся частными называются особыми.

Говорят, что для дифференциального уравнения поставлена задача, если заданы некоторые дополнительные условия, простые случаи задаются начальные значения искомых функций и её производных. То есть ставиться задача Коши.

Например: в задаче (1.1) задаётся начальное количество веществ 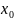, не всегда удаётся найти решение в явном виде.

y=y(x)

Иногда оно задаётся не явно ȹ(x+y)=0 – называется интегральным уравнением. Соответственно при не явном задании общего решения уравнения получится общий интеграл.

Рассмотрим уравнение 1-го порядка разрешенное относительно 1-ой производной. Пусть функция x(y) имеет область определений D ϵ , которое также является определённым уравнением (1.7)

Обычно предполагается , что f непрерывно в D:

y= ϕ (x) xϵ [a; b]

не прерывно и непрерывно дифференцируема на [a; b] такая, что (x, ϕ(x)) ϵ D и выполняется ϕ ‘ (x)= f (x , ϕ(x)) , x ϵ [a, b]

Решение уравнения (1.7) на [a, b]

4) 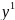=2x

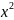y(x)= +c xϵ (-∞; +∞)

y= +2

y= +1

y=

5) = 3

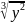
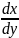= 3 y

* =

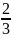
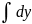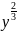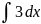
3 y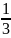 + c =3x

y=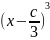

Областью определения является вся плоскость

Заметим, что это уравнение имеет решение y(x)=0, которое нельзя получить из общего выбором константы C.

Геометрическое решение (1.7) y=ϕ(x) соответствует линии лежащей в области D в

и представляет графическую функцию ϕ (x) эта линия - Интегральная линия (1.7)

Так как формула ϕ(x) интегральная линия имеет в каждой точке (x , ϕ(x)) касательную, угловой коэффициент который определяется из уравнения

ϕ ‘ (x)= f (x, ϕ(x))

Очевидно угловой коэффициент можно вычислить в любой точке (x,y) ϵ D не находя самой интегральной кривой.

Выбрав направление векторной касательной, можно сопоставить каждой точке области D некоторой не нулевой векторной_______? так в области D получится направленное поле; и так уравнение (1.7) соответствует в области D векторному полю интегрально направленному.

Задача решения этого уравнения имеет следующею геометрическую интерпретацию:

через каждую точку области D потребуется провести кривую называемую интегральной касательной, в которой каждая точка определяется векторным полем (1.7)

Заметим, что общему решению соответствует семейство кривых , а решение задачи Коши интегрирует кривая проходящая через точку ( , 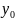) ϵ D

При геометрическом решении уравнения (1.7) можно воспользоваться методом Изоклин.

Изоклины- геометрическое место точки, в каждой точке которой вектор задает направленное поле

f(x, y)= const = k

Различные значения K соответствуют различным изоклинам. B точке пересечения с изоклиной интегрированная линия имеет касательные с угловым коэффициентам K.

6) =

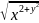
= K

+ =
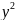