Билет №11

1. Логические функции. Табличное и аналитическое представление логических функций. Таблицы истинности.

1. Формы представления информации.

1) Логическая функция (функция алгебры логики ФАЛ) - функция f(x₁, x₂, … , x_n), принимающая значение , равное нулю или единице на наборе логических переменных x₁, x₂, … , x_n.

Логическую функцию можно задать двумя способами: логической формулой или таблицей истинности. Таблица истинности задаёт значения функции на всех возможных наборах её переменных.

В алгебре логики строго доказывается, что для n переменных количество различных наборов равно2ⁿ ,а количество логических функций для n переменных равно 2 в степени 2ⁿ Рассмотрим все возможные наборы для одной переменной, для двух и трёх переменных.

Для одной переменной таких наборов два:0,1.

Табличное представление логических функций

X1	X2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

1. Конъюнкция (логическое умножение, союз и) – функция f₁(x₁,x₂). Принимает значение истина тогда и только тогда, когда обе переменные истинны. Во всех остальных случаях принимает значение ложь. Обозначается символами: (или знак операции может быть вообще опущен). В общем случае функцию конъюнкция можно определить для n аргументов, т.е. x_1, x_{2, … ,} x_n.

2. Дизъюнкция (логическое сложение, функция ИЛИ) – функция f₇(x_1, x₂). Принимает значение ноль тогда и только тогда, когда оба аргумента равны нулю и принимает значение 1, если хотя бы один аргумент равен 1. Обозначается символом +. В общем случае функцию можно определить для n аргументов.

3. Импликация (следование) х₁ в х₂ функция f₁₃ . Обращается в ноль только в том случае, когда переменная х₁ равна единице, а переменная х₂ равна нулю. Обозначается х₁ х₂.

4. Импликация х₂ в х₁ – функция f₁₁(x₁, x₂). Обращается в ноль тогда и только тогда, когда х₂ равен 1, а х₁ равен 0.

5. Эквиваленция (разнозначность) – функция f₉ (x₁, x₂). Обращается в 1 тогда и только тогда, когда обе переменные одновременно принимают одинаковые значения. Обозначается символами .

6. Исключающее или (сложение по модулю 2), функция f₆ (x₁, x₂). Принимает значение истина в том и только в том случае, когда только один из аргументов равен 1. Обозначается символом .

7. Штрих Шеффера – функция f₁₄ (x₁, x₂). Принимает значение 0 тогда и только тогда, когда оба аргумента одновременно равны 1. Во всех остальных случаях функция равна 1. Обозначается символом /. F₁₄ (x₁, x₂) = x₁ / x_2. Немецкий математик Д. Шеффер на основе этой функции создал алгебру, названную алгеброй Шеффера.

8. Стрелка Пирса (элемент Вебба) – функция f₈ (x₁, x₂). Обозначается символом ↓: f₈ (x₁, x₂) = x₁ ↓ x₂. Математики Ч. Пирс и Д. Вебб независимо друг от друга изучавшие свойства этой функции, создали алгебру, названную алгеброй Пирса (Вебба).

9. Отрицание импликации (коимпликация) х₁ в х₂, функция f₂ (x₁, x₂). Принимает значение 1 тогда и только тогда, когда х₁ равен 1, а х₂ равен 0. Обозначается 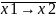, или х₁ х₂. Данную функцию можно рассматривать как функцию запрета со стороны переменной х₂.

10. Отрицание импликации (коимпликация) х₂ в х₁, функция f₄ (x₁, x₂). Принимает значение 1 тогда и только тогда, когда х₂ равен 1, а х₁ равен 0. Во всех остальных случаях значение функции 0. Функцию f₄ (x₁, x₂) можно рассматривать как функцию запрета со стороны переменной х₁.

Оставшиеся шесть логических функций f₀, f₃, f₅, f₁₀, f₁₂, f₁₅ являются либо константами, либо функциями существенным образом зависящие только от одной из переменных х₁ или х₂.

f₀ (x₁, x₂) ≡ 0;

f₁₅ (x₁, x₂) ≡ 1;

f₃ (x₁, x₂) = x₁;

f₅ (x₁, x₂) = x₂;

f₁₂ (x₁, x₂) = ₁;

f₁₀ (x₁, x₂) = ₂.

Аналитическое представление логических функций

Проще выглядит аналитическая запись в виде формул. Но наиболее рациональным является представление логических функций в так называемых нормальных формах. Основу этих формул составляют понятия элементарных конъюнкций и дизъюнкций.

Элементарная конъюнкция (минтерм) образуется конъюнкцией конечного множества логических переменных и их инверсий, например:

Элементарная дизъюнкция (макстерм) образуется дизъюнкцией конечного множества логических переменных и их инверсий, например:

Элементарная конъюнкция принимает единичное значение только при одном из всех возможных наборов входных переменных, а элементарная дизъюнкция принимает нулевое значение только при одном из возможных наборов аргументов и единичное значение при всех других.

Следовательно, минтерм алгебраически представляет собой конъюнкцию аргументов и их инверсий, а макстерм – дизъюнкцию аргументов и их инверсий.

Количество минтермов и макстермов совпадает с количеством возможных наборов аргументов. В таблице 6.2. приведены значения элементарных конъюнкций и дизъюнкций для двух аргументов.

Таблица 6.2. Элементарные конъюнкции и дизъюнкции двух переменных

Значения аргументов			Значения элементарных конъюнкций				Значения элементарных дизъюнкций
X	Y
0	0	0		0	0	1	0	1	1	1
0	1	0		1	0	0	1	1	0	1
1	0	0		0	1	0	1	0	1	1
1	1	1		0	0	0	1	1	1	0

Количество аргументов, образующих элементарную конъюнкцию или дизъюнкцию называется ее рангом. Например, ранг минтерма равен 3.

Если логическая функция представлена дизъюнкцией, конъюнкцией и инверсией, то такая форма представления называется нормальной.

Дизъюнктивная нормальная форма (ДНФ) содержит элементарные конъюнкции, связанные между собой операцией дизъюнкции.

Т.е. нормальная форма – это объединение термов, включающее минтермы переменного ранга.

Количество всех термов, входящих в состав ДНФ равно количеству единичных строк таблицы истинности заданной функции.

Конъюнктивная нормальная форма (КНФ) содержит элементарные дизъюнкции (макстермы), связанные между собой операцией конъюнкции.

Совершенные нормальные формы.

Одну и ту же логическую функцию можно представить различными ДНФ и КНФ. Из всей совокупности нормальных форм выделяют одну ДНФ и одну КНФ, а именно такие формы, которые являются инверсными по отношению друг к другу, т.е. если одна из них равна «1», то другая при этом равна «0», и наоборот. Эти формы называются совершенными нормальными формами.

Дизъюнктивная совершенная нормальная форма (СДНФ) отвечает следующим требованиям:

• в ней нет двух одинаковых элементарных конъюнкций;

• ни одна конъюнкция в ней не содержит одинаковых переменных;

• ни одна конъюнкция не содержит двоичную переменную с ее инверсией;

• все конъюнкции являются элементарными;

• все конъюнкции имеют одинаковый ранг.

Для представления функции в СДНФ может быть использована также операция .

Сформулируем требования, которые предъявляются к операции связывающей элементарные минтермы:

1. Если какой-либо терм = 1, то функция должна быть равна 1.

2. Если какой-либо терм = 0, то функция может быть равна 1.

3. Необходимо, чтобы при значениях термов = 0 функция была равна нулю.

Табличное представление операций отвечающих требованиям имеет вид, представленный в таблицах 6.3. и 6.4.3:

Таблица 6.3. Таблица6.4.

		=+
0	0	0
0	1	1
1	0	1
1	1	1

		=
0	0	0
0	1	1
1	0	1
1	1	0

Любая таблично заданная ФАЛ может быть представлена в следующей аналитической форме:

, где

- элементарный минтерм; знак  обозначает операции +, ;

k – количество наборов, на которых функция равна 1.

Конъюнктивная совершенная нормальная форма (КСНФ) отвечает следующим требованиям:

• в ней нет двух одинаковых элементарных дизъюнкций;

• ни одна дизъюнкция в ней не содержит двух одинаковых переменных;

• ни одна дизъюнкция не содержит переменную вместе с ее инверсией;

• все дизъюнкции имеют один и тот же ранг.

Чтобы определить, какие операции могут связывать элементарные дизъюнкции, изложим следующие требования:

1. Если какой-либо терм = 0, то функция должна быть равна 0.

2. Если все термы = 0, то функция равна 1.

Выполняя эти требования можно привести к операциям конъюнкции и равнозначности (таблица 6.5. и 6.6):

Таблица 6.5. Таблица 6.6.

		
0	0	0
0	1	0
1	0	0
1	1	1

		
0	0	1
0	1	0
1	0	0
1	1	1

Вывод: любая таблично заданная ФАЛ может быть задана в аналитической форме:

, где

знак  обозначает операции  и , k – количество двоичных наборов, для которых =0.

В алгебре логики строго доказывается, что любая логическая функция, кроме , представима в ДСНФ, любая функция, кроме , представима в КСНФ.

Формулы в ДСНФ или КСНФ можно получить по табличному представлению логической функции.

Для образования ДСНФ необходимо выполнить следующие действия:

• по каждому набору двоичных переменных, при котором логическая функция принимает значение 1, составить элементарные конъюнкции;

• в элементарные конъюнкции записать без инверсии переменные, заданные единицей в соответствующем наборе, и с инверсией – переменные заданные нулем;

• соединить элементарные конъюнкции знаком операции дизъюнкции или операции сложение по модулю 2.

• Для образования КСНФ необходимо выполнить аналогичную последовательность действий:

• по каждому набору двоичных переменных, при котором логическая функция принимает значение 0, составить элементарные дизъюнкции;

• в элементарные дизъюнкции записать без изменения переменные, заданные нулем в соответствующем наборе, и с инверсией – переменные заданные единицей;

• соединить элементарные дизъюнкции знаком конъюнкции.

2) Формы представления информации

• Текстовая информация

• Числовая информация [В чистом виде числовая информация встречается редко. Чаще всего используется комбинированная форма представления информации].

• Графическая информация.

• Звуковая информация.