2) Мера информации.

Термин «информация» имеет много определений. В широком смысле

информация — отражение реального мира. Существует определение термина

в узком смысле: информация —любые сведения, являющиеся объектом

хранения, передачи и преобразования. Оба определения важны для по-

нимания процессов функционирования вычислительной машины.

Важный вопрос теории передачи и преобразования информации —

установление меры, количества и качества информации.

Информационные меры, как правило, рассматриваются в трех аспектах:

структурном, статистическом и семантическом.

В структурном аспекте рассматривается строение массивов информации

и их измерение простым подсчетом информационных элементов или

комбинаторным методом. Структурный подход применяется для оценки

возможностей информационных систем вне зависимости от условий их

применения.

При статистическом подходе используется понятие энтропии как меры

неопределенности, учитывающей вероятность появления и информативность

того или иного сообщения. Статистический подход учитывает

конкретные условия применения информационных систем. Семантический подход позволяет выделить полезность или ценность информационного сообщения.

Американский инженер З. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперед заданного множества из N равновероятных сообщений, а количество информации I, содержащейся в выбранном сообщении, определял по формуле:

Формула Хартли

I=log₂N.

Отсюда следует, что 2^I=N.

Рассмотрим пример: допустим нужно угадать число из набора целых чисел от нуля до 63. В соответствии с формулой Хартли количество информации в сообщении о том, какое число угадано равно I=log₂64=6 бит.

Формула Хартли определяет длину двоичного слова (I), которое требуется для кодирования N равновероятных сообщений (объектов, состояний, событий).

Такой подход для определения количества информации назвали вероятностным. Рассмотрим с этой точки зрения формулу Хартли.

Пусть N – число равновероятных событий. Поскольку вероятности появления событий равны, то можно записать р=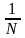 , следовательно N= . Исходя из этого, запишем формулу Хартли в следующем виде:

I=log₂N=log₂(1/p)=-log₂p.

Следует учесть, что не все события могут быть равновероятны.

События можно рассматривать как возможные исходы некоторого

опыта, причем все исходы этого опыта составляют ансамбль, или полную

группу событий. К. Шеннон ввел понятие неопределенности ситуации, воз-

никающей в процессе опыта, назвав ее энтропией. Энтропия ансамбля есть

количественная мера его неопределенности и, следовательно, информативности количественно выражаемая как средняя функция множества вероят-

ностей каждого из возможных исходов опыта.

Формула Шеннона.

I=-(p₁log₂p₁+p₂log₂p₂+…p_Nlog₂p_N),

где р_i – вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.

Итак , в качестве единицы информации условились принять один бит. Это то количество информации, которое необходимо для различения двух равновероятных событий. В вычислительной технике бит (разряд) – это наименьший объем памяти, необходимый для хранения одного из двух чисел «0» или «1».

Билет №6

1. Компьютерное представление вещественных чисел. Нормализованная запись числа. Представление чисел с плавающей точкой.

2. Аналитическое представление функций алгебры логики.

1) Представление чисел с плавающей точкой.

Для представления вещественных чисел в памяти ЭВМ используется формат с плавающей точкой. При этом необходимо помнить, что система вещественных чисел представимых в ЭВМ является дискретной и конечной.

В общем случае любое число N, представляемое в форме с плавающей точкой, является произведением двух сомножителей: 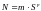. m — мы будем называть мантиссой числа (модуль целой части мантиссы изменяется в диапазоне от 1 до S-1 (включая эти числа), где S- основание системы счисления),

p — целочисленный порядок,

S  основание системы счисления.

Различают нормализованную и экспоненциальную формы записи числа. Если мантисса является правильной дробью, у которой первая цифра после точки отлична от нуля , то число называется нормализованным.

При представлении числа в экспоненциальной форме обязательно присутствует целая часть, содержащая не более одной цифры отличной от нуля, фактически эта форма представления совпадает со стандартной математической формой записи числа.

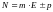
Вещественное число в ПЭВМ представлено в экспоненциальной форме.

Следовательно, при представлении чисел с плавающей точкой необходимо записать в разрядной сетке ЭВМ со своими знаками мантиссу 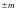и порядок . Знак числа при этом совпадает со знаком мантиссы. Запишем число 314.6789 в экспоненциальной форме:314.6789= 3.1467890000E+2. Число разрядов, выделенных для изображения порядков, определяет диапазон представимых в ЭВМ чисел с плавающей точкой.

Кроме того, этот диапазон зависит также от основания S принятой системы счисления.

Значение произвольного числа вещественного типа представляется в ПЭВМ лишь с некоторой конечной точностью, которая зависит от внутреннего формата вещественного числа, точность представления чисел повышается с увеличением числа разрядов мантиссы.

Для того, чтобы упростить операции над порядками их сводят к действиям над целыми положительными числами путем использования так называемого смещенного порядка, который всегда положителен. смещенный порядок получается путем прибавления к порядку р некоторого целого положительного числа, значение которого зависит от конкретного формата данных.

Десятичная точка подразумевается перед левым (старшим) разрядом мантиссы, но при действиях с числом ее положение смещается влево или вправо в зависимости от двоичного порядка.

Рассмотрим представление чисел в разрядной сетке длиной 4 байта ( так называемая одинарная точность). Изобразим разрядную сетку, состоящую из 32 разрядов и посмотрим, как эти разряды распределены.

0 1 2 3 4 5 6 7 8 … 31

…

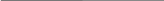
знак мантиссы порядок мантисса

Пусть необходимо представить число –13,75 в разрядной сетке с одинарной точностью. Для этого необходимо выполнить следующие действия:

1. перевести число в двоичную систему счисления;

2. представить его в экспоненциальной форме;

3. получить исходный порядок и мантиссу;

4. получить смещенный порядок.

Для решения обратной задачи необходимо выполнить следующие действия:

1. Перевести шестнадцатеричное число в двоичную систему счисления.

2. Выделить знак мантиссы(знак мантиссы совпадает со знаком числа).

3. Выделить смещенный порядок.

4. Вычислить исходный порядок.

5. Записать число, не забыв указать его целую часть, в экспоненциальной форме.

6. Перевести число из экспоненциальной формы в обычную форму записи.

7. Перевести число из двоичной системы счисления в десятичную.

Выполним перечисленные действия.

Операция алгебраического сложения чисел, представленных в форме с плавающей точкой , производится несколько сложнее, чем для чисел, представленных в форме с фиксированной точкой. При выполнении ее сначала выравниваются порядки слагаемых, В результате сравнения порядков порядок меньшего по модулю числа принимается равным порядку большего, а его мантисса сдвигается вправо на число шестнадцатеричных разрядов, равное разности порядков.

В процессе сдвига мантиссы меньшего слагаемого происходит потеря младших разрядов, что вносит определенную погрешность в результат выполнения данной операции.

После выравнивания порядков производится алгебраическое сложение мантисс.